
- •П.2 Математический маятник.
- •П.3 Физический маятник.
- •Свободные колебания.
- •Период и частота колебаний.
- •Кинематика и динамика свободных гармонических колебаний.
- •Вектор – амплитуда.
- •Сложение гармонических колебаний.
- •П.1 Одинаково направленные колебания различной частоты.
- •Взаимно перпендикулярные колебания.
- •Ангармонические (негармонические) колебания.
- •Свободные затухающие колебания.
- •Энергия затухающих колебаний.
- •Характеристики затухающих колебаний.
- •Апериодическое движение.
- •Дифференциальное уравнение для колебательного контура.
- •Свободные колебания в контуре без сопротивления.
- •Свободные затухающие колебания в контуре с сопротивлением.
- •Заряд, напряжение, ток, энергия в колебательном контуре с сопротивлением.
- •Переменный ток.
- •Мощность в цепи переменного тока.
- •Возникновение и распространение упругой волны.
- •Уравнение волны.
- •П.1 уравнение плоской гармонической волны.
- •П.2 Уравнение сферической гармонической волны.
- •П.3 Уравнение плоской гармонической волны, распространяющейся в произвольном направлении.
- •Волновое уравнение.
- •Скорость упругой волны в твердой среде.
- •Скорость упругой волны в газе.
- •Скорость упругой волны в однородном контуре.
- •Энергия упругой волны.
- •Плотность потока энергии.
- •Интенсивность волны.
- •Стоячие волны.
- •Узлы и пучности стоячей волны.
- •Поток энергии в стоячей волне.
- •Скорость упругой волны в однородном шнуре.
- •Колебания струны.
- •Эффект Доплера для звуковых волн.
- •Электрические волны.
- •Плоская электромагнитная волна.
- •Энергия электромагнитной волны.
- •Плотность потока энергии электромагнитной волны.
- •Интенсивность волны.
- •Импульс электромагнитной волны.
- •Давление электромагнитной волны.
- •Излучение электромагнитных волн.
- •Эффект Доплера для электромагнитных волн.
Часть: Колебания и волны.
Процессы, повторяющиеся во времени называются колебаниями или колебательными процессами.
Тело или система, участвующие в колебательном процессе, называются колебательной системой или осциллятором.
Глава: Механические колебания.
Маятники.
Рассмотрим три механические колебательные системы, которые называются маятниками.
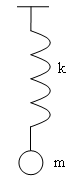
п.1 Пружинный маятник.
Пружинный маятник
представляет собой цилиндрическую
пружинку жесткостью
![]() ,
закрепленную одним концом. К другому
концу прикреплен грузик массой
,
закрепленную одним концом. К другому
концу прикреплен грузик массой
![]() .
Если оттянуть грузик и отпустить, то
начнутся колебания. Выберем ось
.
Если оттянуть грузик и отпустить, то
начнутся колебания. Выберем ось
![]() так, чтобы ее начало совпадало с положением
груза когда пружина не деформирована.
так, чтобы ее начало совпадало с положением
груза когда пружина не деформирована.
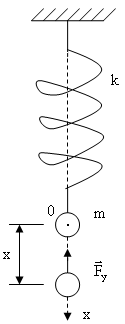
Будем считать пружину невесомой, а силу тяжести, действующую на грузик много меньшей силы упругости пружины. Запишем уравнение 2-го закона Ньютона для грузика.
![]() ,
,
![]() .
.
Спроецируем на ось
![]() ,
,
![]() ,
,
![]() ,
,
где - деформация пружины и координата грузика
![]() ,
,
![]() .
.
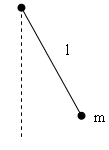
П.2 Математический маятник.
Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити или невесомом подвесе.
Материальная точка
массой
подвешена на нити длиной
![]() .
Пусть маятник движется, как показано
на рисунке.
.
Пусть маятник движется, как показано
на рисунке.
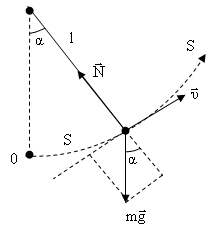
Обозначим:
![]() -
путь, пройденный материальной точкой,
отсчитанный от положения равновесия 0
вдоль траектории.
-
путь, пройденный материальной точкой,
отсчитанный от положения равновесия 0
вдоль траектории.
Запишем 2-й закон Ньютона
![]() .
.
Спроецируем
уравнение на ось, совпадающую с
направлением мгновенной скорости
![]()
![]() .
.
Выразим угол
![]() через длину дуги
длину маятника
.
Запишем
через длину дуги
длину маятника
.
Запишем
![]()
![]()
Далее
![]() ,
,
![]() ,
,
![]() .
.
Пусть выполняется условие малых отношений маятника:
![]() ,
,
![]() ,
,
![]() .
.
Тогда получим уравнение:
![]() .
.
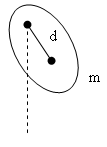
П.3 Физический маятник.
Твердое тело
подвешено на горизонтальной оси
![]() и может свободно вращаться относительно
нее. Точка
называется точкой подвеса.
и может свободно вращаться относительно
нее. Точка
называется точкой подвеса.
Если наклонить тело от вертикали, то начнется колебательное движение.
Обозначим
![]() -
центр масс. Проведем отрезок
-
центр масс. Проведем отрезок
![]() и обозначим его длину
и обозначим его длину
![]() .
Проведем вертикаль через точку
.
Обозначим угол между вертикалью и
,
отсчитанный от вертикали
.
Проведем вертикаль через точку
.
Обозначим угол между вертикалью и
,
отсчитанный от вертикали
![]() .
Масса тела равна
.
.
Масса тела равна
.
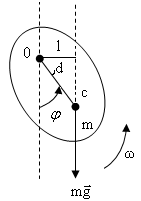
Рассмотрим основное уравнение динамики твердого тела для указанного положения маятника
![]() .
.
Направление оси
вращения и вектора
![]() указано на рисунке.
указано на рисунке.
Здесь:
![]() -
проекция момента силы
относительно точки
на ось вращения.
-
проекция момента силы
относительно точки
на ось вращения.
![]() - момент инерции
относительно той же оси.
- момент инерции
относительно той же оси.
Запишем:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим малые колебания, удовлетворяющие условию
![]() ,
,
![]() .
.
Тогда
![]() .
.
Свободные колебания.
Колебания, возникающие в отсутствие переменных внешних воздействий на осциллятор, называются свободными.
Полученные выше уравнения можно записать в общем виде
![]() ,
,
где - величина, определяющая отклонение маятника от положения равновесия или смещение маятника,
![]() - величина,
характеризующая систему.
- величина,
характеризующая систему.
Решение уравнения ищем в виде:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() - мнимая единица.
- мнимая единица.
Общее решение дифференциального уравнения имеет вид
![]() .
.
Итак, получим решение в виде
![]() ,
,
![]()
где
![]() ,
,
![]() - некоторые константы.
- некоторые константы.
После дальнейших преобразований можно привести к виду
![]() .
.
![]()
Здесь:
- смещение
осциллятора в момент
![]() ,
,
![]() - амплитуда
колебаний,
- амплитуда
колебаний,
![]() ,
,
![]() -
круговая (циклическая) частота колебаний
или собственная (круговая) частота
системы,
-
круговая (циклическая) частота колебаний
или собственная (круговая) частота
системы,
![]() ,
,
![]() - фаза колебаний,
- фаза колебаний,
![]() ,
,
- начальная фаза колебаний или фаза колебаний в начальный (нулевой) момент времени, .
Найдем модуль максимального смещения осциллятора.
![]() .
.
Амплитуда колебаний численно равна модулю максимального смещения осциллятора от положения равновесия.
Для нахождения
амплитуды
и начальной фазы
необходимо знать начальные условия,
т.е. значение в момент
![]() ,
например,
,
например,
![]() и
и
![]() .
.
![]()
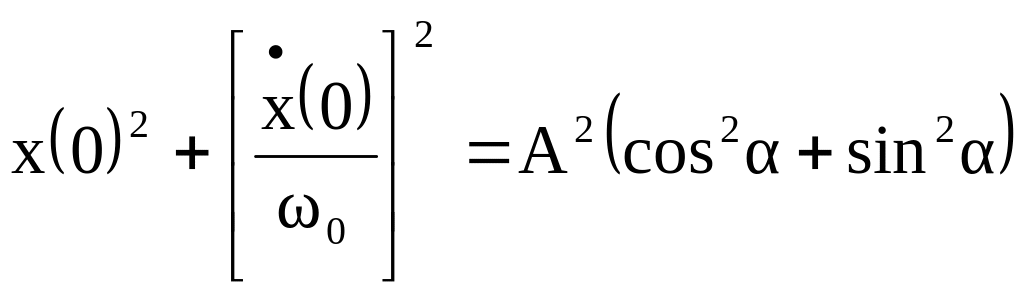 ,
,
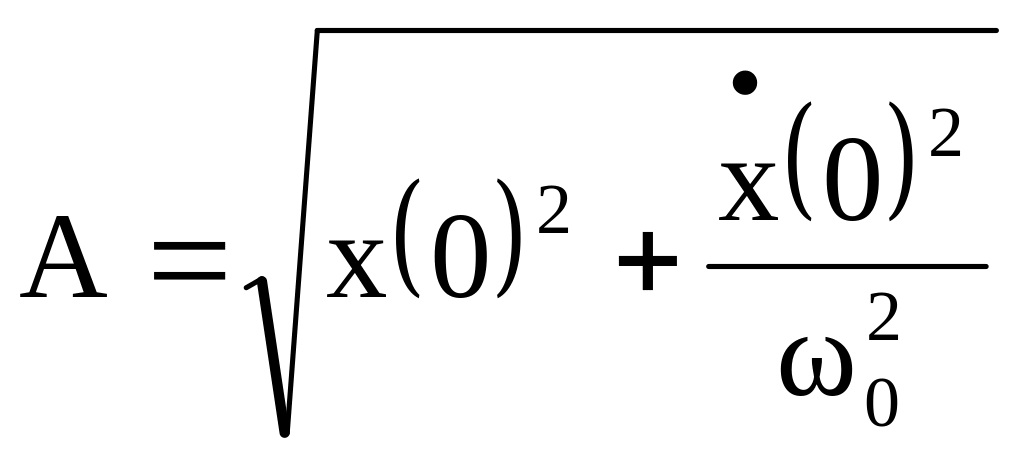 ,
,
![]() ,
,
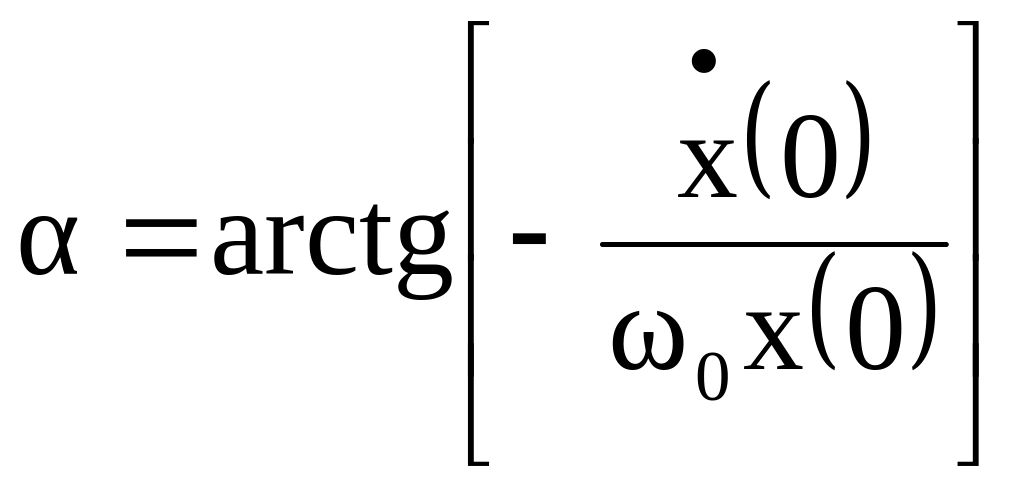 .
.
Фазу колебаний будем обозначать:
![]() .
.
Начальная фаза равна:
![]() ,
,
![]() .
.
Функции в математике называются гармоническими. В дальнейшем будем использовать функцию, содержащую косинус.
Период и частота колебаний.
Возьмем приращение фазы колебаний
![]() .
.
Пусть за отрезок
времени
![]() приращение фазы оказалось равным
приращение фазы оказалось равным
![]() .
Обозначим
.
Обозначим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
Отрезок времени, в течение которого приращение фазы колебаний составляет , называется периодом колебаний.
Величина
![]() есть период свободных гармонических
колебаний.
есть период свободных гармонических
колебаний.
Очевидно, что
![]() .
.
Обозначим
![]() - смещение в момент
.
Найдем смещение в момент
- смещение в момент
.
Найдем смещение в момент
![]() .
.
![]()
![]() .
.
За время равное периоду колебаний система совершает одно колебание.
Величина, обратная периоду колебаний, называется частотой колебаний
![]() ,
,
![]() .
.
Частота колебаний численно равна числу колебаний, совершаемых системой в единицу времени, т.е. в 1 секунду.
Запишем:
![]()
![]() .
.
В заключение дадим в виде таблички основные характеристики рассмотренных маятников.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]()
