
- •Глава 1. Основные понятия теории вероятностей
- •1.1 Классификация событий. Действия над событиями
- •1.2. Относительная частота
- •1.3. Классическое определение вероятности
- •1.4. Элементы комбинаторики
- •Примеры решения задач
- •Глава 2. Основные теоремы теории вероятностей
- •2.1 Сложение и умножение вероятностей
- •Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло:
- •Свойства:
- •1. Вероятность произведения n событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
- •2.2 Формула полной вероятности. Формула Байеса
- •Примеры решения задач
- •Глава 3. Повторные испытания
- •3.1 Формула Бернулли
- •3.2 Предельные теоремы Лапласа и Пуассона
- •Примеры решения задач
- •Глава 4. Дискретные случайные величины
- •4.1. Дискретные случайные величины.
- •4.2. Числовые характеристики дискретных случайных величин.
- •1. Математическое ожидание.
- •2. Дисперсия случайной величины.
- •3. Среднее квадратическое (стандартное) отклонение.
- •4. Моменты случайных величин.
- •5. Характеристики формы распределения.
- •4.3. Числовые характеристики меры связи случайных величин.
- •1. Ковариация.
- •2. Корреляция.
- •4.4. Распределения дискретных случайных величин.
- •1. Равномерное распределение.
- •2. Геометрическое распределение.
- •4. Биномиальное распределение.
- •5. Распределение Пуассона.
- •Примеры решения задач
- •Глава 5. Непрерывные случайные величины.
- •5.1. Функция распределения случайной величины
- •5.2. Плотность распределения вероятностей.
- •Связь между функцией распределения и плотностью распределения вероятностей.
- •5.3. Числовые характеристики непрерывных случайных величин
- •Примеры решения задач
- •Глава 6. Распределения непрерывных случайных величин
- •6.1. Равномерное распределение.
- •6.2. Показательное (экспоненциальное) распределение.
- •6.3. Нормальное распределение
- •Примеры решения задач
Примеры решения задач
5.1. Случайная величина X задана функцией распределения
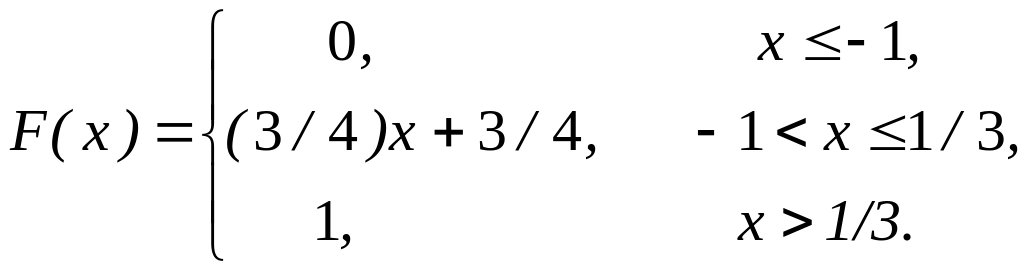
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).
Решение: Вероятность того, что Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале: Р (а < Х < b) = F (b)—F (а). Положив a=0, b= 1/3, получим
Р (0 < Х < 1/3)=F(1/3)—F(0)=[(3/4)x+3/4]x=1/3 – F[(3/4)x+3/4]x=0=l/4.
5.2.
Случайная величина Х
задана на всей оси Ох
функцией
распределения F
(х)![]() .
Найти
возможное значение х1,
удовлетворяющее условию: с вероятностью
1/4 случайная величина Х
в результате испытаний примет значение,
большее х1.
.
Найти
возможное значение х1,
удовлетворяющее условию: с вероятностью
1/4 случайная величина Х
в результате испытаний примет значение,
большее х1.
Решение:
События
![]() и X>x1
– противоположные, поэтому
и X>x1
– противоположные, поэтому
![]() .
Следовательно,
.
Следовательно,
![]()
Т. к. P(X=x)=0, то
![]()
По определению функция распределения,
![]()
Следовательно,
![]() или
или
![]()
Отсюда
![]() ,
или
,
или
![]() .
.
5.3.
Непрерывная
случайная величина Х
задана плотностью распределения
![]() в интервале
в интервале
![]() ;
вне этого интервала f(x)=0.
Найти вероятность того, что Х
примет значение, принадлежащее интервалу
;
вне этого интервала f(x)=0.
Найти вероятность того, что Х
примет значение, принадлежащее интервалу
![]() .
.
Решение:
Воспользуемся формулой (5.6) P(a Х b) =
.
По условию
![]() ,
,
![]() .
Следовательно, искомая вероятность
.
Следовательно, искомая вероятность
![]() .
.
5.4. Задана плотность распределения непрерывной случайной величины Х
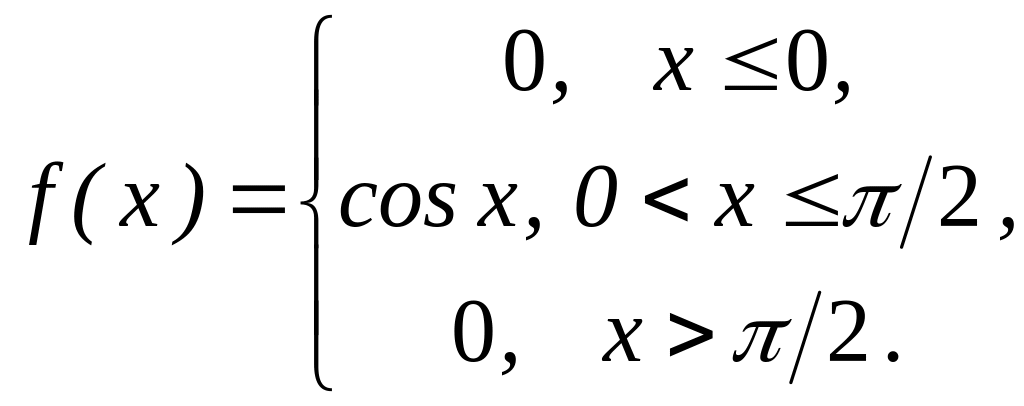
Найти функцию распределения F(x).
Решение: Используем формулу (5.7)
Если
х![]() 0,
то f(x)=0,
следовательно,
0,
то f(x)=0,
следовательно,
![]() .
.
Если
![]() ,
то
,
то
![]()
Если
х>![]() ,
то
,
то
![]()
Итак, искомая функция распределения
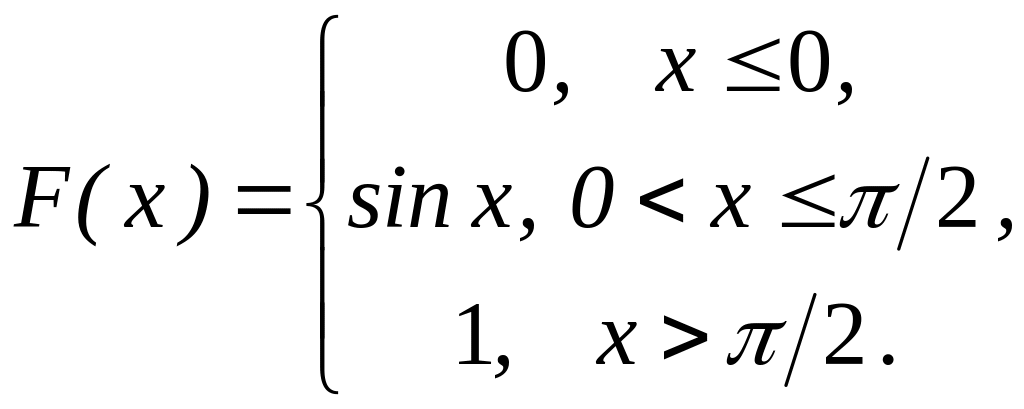
5.5. Случайная величина Х задана плотностью распределения f(x)=2x в интервале (0,1); вне этого интервала f(x)=0. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение величины Х.
Решение: Используем формулы (5.8б), (5.12)
![]() ,
,
![]()
Подставив а=0, b=1, f(x)=2x, получим
![]() и
и
![]()
Т.к.
,
то
![]() .
.
Глава 6. Распределения непрерывных случайных величин
6.1. Равномерное распределение.
В качестве примера рассмотрим случайную величину Х, равномерно распределённую на промежутке [a; b]. В этом случае f(х) постоянна внутри этого промежутка:
a
b
f(x)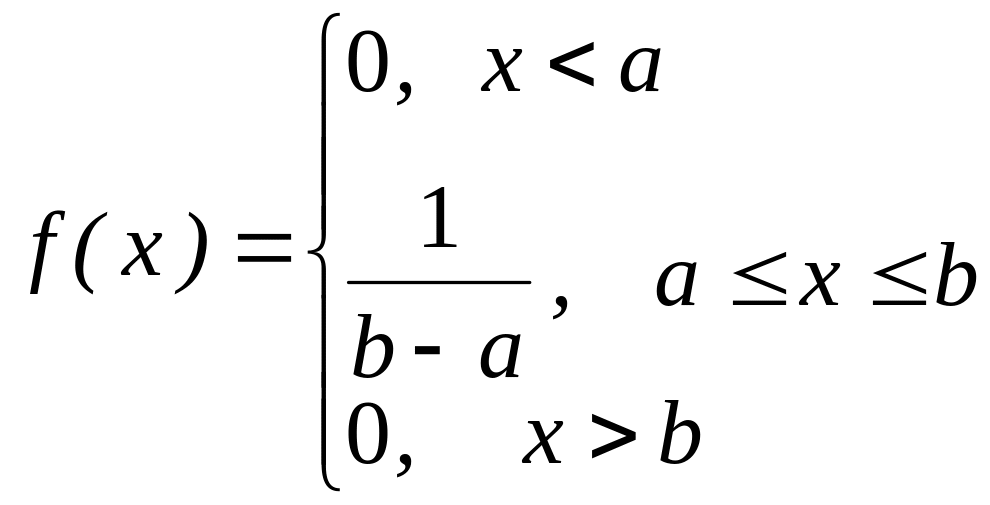
Г
Рис. 6.1
Для равномерного распределения функция F(x) имеет вид:

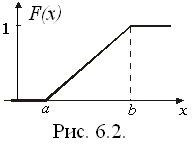 (6.2)
(6.2)
График функции F(x) представлен на рисунке 6.2.
Математическое
ожидание равномерно распределенной
непрерывной случайной величины равно
![]() .
В силу симметричности равномерного
распределения медиана равна
.
В силу симметричности равномерного
распределения медиана равна
![]() ,
моды нет.
,
моды нет.
Дисперсия
равномерного распределения равно
![]() .
Стандартное отклонение
.
Стандартное отклонение
![]() .
.
Асимметрия
равномерного распределения равна нулю
![]() ,
эксцесс равен
,
эксцесс равен
![]() .
.
Вероятность
попадания равномерно распределенной
случайной величины в интервал
![]() определяется по формуле:
определяется по формуле:
![]() (6.3)
(6.3)
6.2. Показательное (экспоненциальное) распределение.
Показательным (экспоненциальным) распределением называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью вероятностей:
![]() , (6.4)
, (6.4)
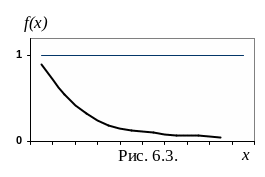
г
![]() - постоянная и называется параметром
показательного распределения. График
плотности распределения представлен
на рисунке 6.3.
- постоянная и называется параметром
показательного распределения. График
плотности распределения представлен
на рисунке 6.3.
 Функция
распределения
Функция
распределения
![]() случайной
величины, распределенной по показательному
закону, равна:
случайной
величины, распределенной по показательному
закону, равна:
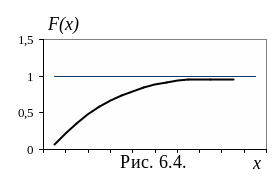
![]() (6.5)
(6.5)
График функции распределения приведен на рисунке 6.4.
Математическое
ожидание случайной величины, распределенной
по показательному закону, равно M(X)=![]() .
Медиана –
.
Медиана –
![]() .
Дисперсия – D(X)=
.
Дисперсия – D(X)=![]() .
Среднее квадратическое отклонение
совпадает с математическим ожиданием
и равно
.
Среднее квадратическое отклонение
совпадает с математическим ожиданием
и равно
![]() (X)=
.
Коэффициент асимметрии равен A(X)=2,
эксцесс
– Е(Х)=6.
(X)=
.
Коэффициент асимметрии равен A(X)=2,
эксцесс
– Е(Х)=6.
Вероятность попадания случайной величины, распределенной по показательному закону, в интервал определяется по формуле:
![]() (6.6)
(6.6)
