
- •Глава 1. Основные понятия теории вероятностей
- •1.1 Классификация событий. Действия над событиями
- •1.2. Относительная частота
- •1.3. Классическое определение вероятности
- •1.4. Элементы комбинаторики
- •Примеры решения задач
- •Глава 2. Основные теоремы теории вероятностей
- •2.1 Сложение и умножение вероятностей
- •Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло:
- •Свойства:
- •1. Вероятность произведения n событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
- •2.2 Формула полной вероятности. Формула Байеса
- •Примеры решения задач
- •Глава 3. Повторные испытания
- •3.1 Формула Бернулли
- •3.2 Предельные теоремы Лапласа и Пуассона
- •Примеры решения задач
- •Глава 4. Дискретные случайные величины
- •4.1. Дискретные случайные величины.
- •4.2. Числовые характеристики дискретных случайных величин.
- •1. Математическое ожидание.
- •2. Дисперсия случайной величины.
- •3. Среднее квадратическое (стандартное) отклонение.
- •4. Моменты случайных величин.
- •5. Характеристики формы распределения.
- •4.3. Числовые характеристики меры связи случайных величин.
- •1. Ковариация.
- •2. Корреляция.
- •4.4. Распределения дискретных случайных величин.
- •1. Равномерное распределение.
- •2. Геометрическое распределение.
- •4. Биномиальное распределение.
- •5. Распределение Пуассона.
- •Примеры решения задач
- •Глава 5. Непрерывные случайные величины.
- •5.1. Функция распределения случайной величины
- •5.2. Плотность распределения вероятностей.
- •Связь между функцией распределения и плотностью распределения вероятностей.
- •5.3. Числовые характеристики непрерывных случайных величин
- •Примеры решения задач
- •Глава 6. Распределения непрерывных случайных величин
- •6.1. Равномерное распределение.
- •6.2. Показательное (экспоненциальное) распределение.
- •6.3. Нормальное распределение
- •Примеры решения задач
Глава 3. Повторные испытания
3.1 Формула Бернулли
Повторными называются испытания, в которых вероятность появления события в каждом испытании постоянна и не зависит от исходов других испытаний.
Считаем,
что испытания происходят в одинаковых
условиях и вероятность появления события
в каждом испытании одна и та же и равна
,
а вероятность непоявления события
![]() .
.
Вероятность
того, что в
![]() независимых испытаниях событие
наступит ровно
независимых испытаниях событие
наступит ровно
![]() раз выражается формулой
Бернулли
раз выражается формулой
Бернулли
![]() , (3.1)
, (3.1)
где
![]() .
.
Число
![]() называется наивероятнейшим
числом
появления события
в
испытаниях, если вероятность того, что
событие наступит в этих испытаниях
раз, не меньше вероятности остальных
возможных исходов испытаний. При заданных
и
наивероятнейшее число
определяют из двойного неравенства
называется наивероятнейшим
числом
появления события
в
испытаниях, если вероятность того, что
событие наступит в этих испытаниях
раз, не меньше вероятности остальных
возможных исходов испытаний. При заданных
и
наивероятнейшее число
определяют из двойного неравенства
![]() . (3.2)
. (3.2)
3.2 Предельные теоремы Лапласа и Пуассона
Если
число испытаний велико
![]() ,
то вероятность появления события А в k
раз в n
испытаниях можно рассчитать с помощью
предельных теорем.
,
то вероятность появления события А в k
раз в n
испытаниях можно рассчитать с помощью
предельных теорем.
Локальная
теорема Лапласа. Если
вероятность появления события
в каждом из
независимых испытаний равна одной и
той же постоянной
![]() и велика (р>0,1),
то вероятность того, что во всех этих
испытаниях событие
появится ровно
раз, приближенно выражается формулой
и велика (р>0,1),
то вероятность того, что во всех этих
испытаниях событие
появится ровно
раз, приближенно выражается формулой
![]() , (3.3)
, (3.3)
где
![]() ,
,
![]() . (3.4)
. (3.4)
Функция
![]() четная, следовательно,
четная, следовательно,
![]() .
.
Интегральная
теорема Лапласа. Если
вероятность появления события
в каждом из
независимых испытаний равна одной и
той же постоянной
и велика (р>0.1),
то вероятность того, что во всех этих
испытаниях событие
появится менее
![]() раз
и не более
раз
и не более
![]() раз, приближенно равна
раз, приближенно равна
![]() , (3.5)
, (3.5)
где
![]() – функция Лапласа, т.е.
– функция Лапласа, т.е.
![]() ,
а
,
а
![]() и
и
![]() определяются равенствами
определяются равенствами
![]() ,
,
![]() . (3.6)
. (3.6)
Функция
Лапласа нечетная, следовательно,
![]() .
Для значений
.
Для значений
![]() полагают
полагают
![]() .
.
Теорема Пуассона. Если число испытаний велико, а вероятность появления события в каждом испытании очень мала (р<0,1), то говорят, что случайная величина распределена по закону Пуассона и используют приближенную формулу
![]() , (3.7)
, (3.7)
где
– число появлений события в
независимых испытаниях,
![]() – среднее число появлений события в
испытаниях.
– среднее число появлений события в
испытаниях.
Примечания.
Формулы Бернулли, Лапласа и Пуассона применяются в тех случаях, когда рассматриваются испытания, удовлетворяющие схеме Бернулли.
Приближенными формулами Лапласа на практике пользуются в случае, если
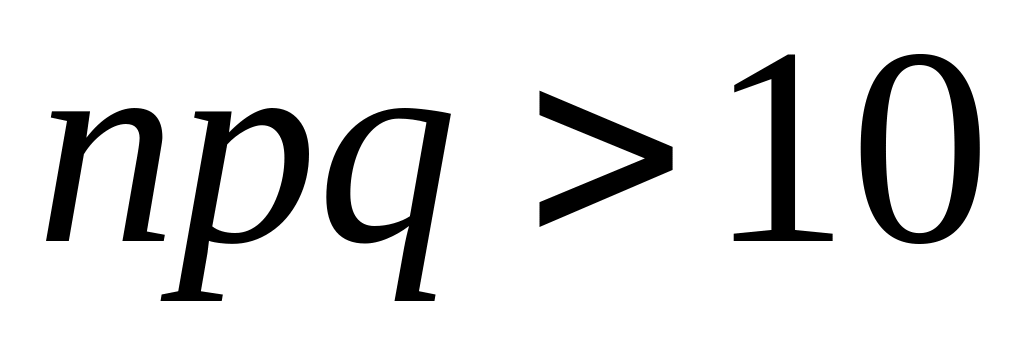 .
Если же
.
Если же
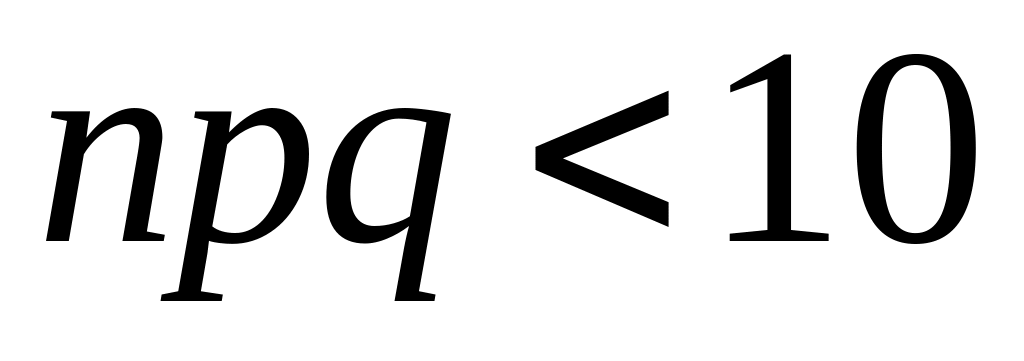 ,
то эти формулы приводят к большим
погрешностям.
,
то эти формулы приводят к большим
погрешностям.
Примеры решения задач
3.1. Прибор состоит из 6 узлов. Вероятность отказа в течение месяца для каждого узла равна 0,8. Узлы выходят из строя независимо один от другого. Найти вероятность того, что в течение месяца: а) откажет ровно один узел; б) откажут ровно два узла; в) откажет не менее двух узлов.
Решение.
а)
По условию задачи
![]() 6,
6,
![]() 1,
1,
![]() 0,8,
0,8,
![]() 0,2.
0,2.
По
формуле Бернулли
![]() =0,001536
=0,001536
б) 6, 2, 0,8, 0,2
![]() =0,01536
=0,01536
в)
![]() =
=![]()
![]() =1–0,000064–0,00154=0,998.
=1–0,000064–0,00154=0,998.
3.2. Магазин получил партию из 50 мониторов. Вероятность наличия в партии монитора со скрытыми дефектами равна 0,05. Найти наивероятнейшее число мониторов с дефектами в этой партии.
Решение. Проводится 50 повторных независимых испытаний. Вероятность наличия монитора со скрытыми дефектами в каждом испытании постоянна. Значит выполняется схема Бернулли. По формуле (3.4) имеем:
50![]() 0,05–0,95
0,05–0,95![]() 50
0,05+0,05,
50
0,05+0,05,
1,55 2,55.
Так как число мониторов может быть только целым, то наивероятнейшее число мониторов со скрытыми дефектами в этой партии равно 2.
3.3. Завод отправил на продажу 5000 хрустальных ваз. Вероятность того, что в пути разбили одну вазу равна 0,0002. Найти вероятность того, что в пути будет разбито: а) три вазы; б) не более трех ваз.
Решение. Т.к. число независимых испытаний =5000 велико, а вероятность =0,0002 появления события в каждом испытании мала, то для вычисления вероятности появления события раз применяем формулу Пуассона, где =5000 0,0002=1.
а)
при
=3
получаем:
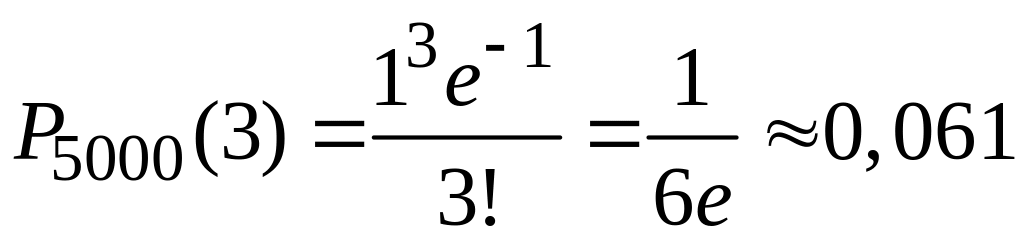 ;
;
б)
![]() =
=
= .
.
3.4. Из каждых 100 студентов, имеющих компьютеры, 40 имеют выход в Интернет. Найти вероятность того, что: а) из 600 студентов, имеющих компьютеры, 210 имеют выход в Интернет; б) из 600 студентов, имеющих компьютеры, от 210 до 260 включительно имеют выход в Интернет.
Решение.
а) Вероятность
того, что студент имеет выход в Интернет,
равна 0,4. Так как
![]() =144>10,
то применим локальную формулу Лапласа.
Вначале по формуле (3.7) находим
=144>10,
то применим локальную формулу Лапласа.
Вначале по формуле (3.7) находим
![]() .
.
Функция
четная, следовательно,
![]() .
Пользуясь таблицей значений функции
находим, что
.
Пользуясь таблицей значений функции
находим, что
![]() =0,0175.
По формуле (3.6) получаем
=0,0175.
По формуле (3.6) получаем
![]() .
.
б) Применяем интегральную теорему Лапласа. Вначале по формулам (3.9) находим
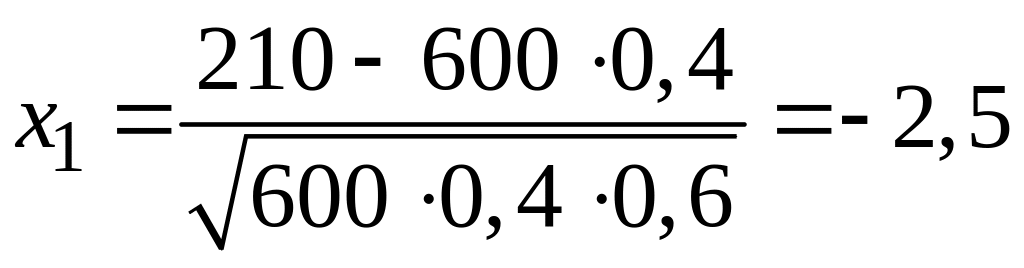 ,
,
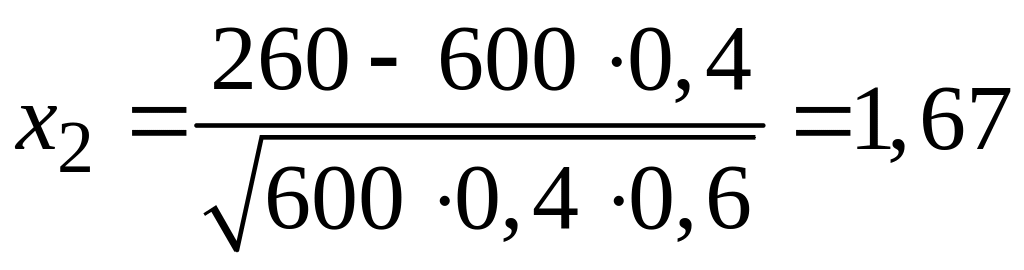 .
.
Теперь по формуле (3.8), учитывая свойства функции и таблицу значений функции , получаем
![]() 0,4525+0,4938=0,946
0,4525+0,4938=0,946
