
- •Глава 1. Основные понятия теории вероятностей
- •1.1 Классификация событий. Действия над событиями
- •1.2. Относительная частота
- •1.3. Классическое определение вероятности
- •1.4. Элементы комбинаторики
- •Примеры решения задач
- •Глава 2. Основные теоремы теории вероятностей
- •2.1 Сложение и умножение вероятностей
- •Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже произошло:
- •Свойства:
- •1. Вероятность произведения n событий равна произведению одного из них на условные вероятности всех остальных, вычисленные в предположении, что все предыдущие события наступили:
- •2.2 Формула полной вероятности. Формула Байеса
- •Примеры решения задач
- •Глава 3. Повторные испытания
- •3.1 Формула Бернулли
- •3.2 Предельные теоремы Лапласа и Пуассона
- •Примеры решения задач
- •Глава 4. Дискретные случайные величины
- •4.1. Дискретные случайные величины.
- •4.2. Числовые характеристики дискретных случайных величин.
- •1. Математическое ожидание.
- •2. Дисперсия случайной величины.
- •3. Среднее квадратическое (стандартное) отклонение.
- •4. Моменты случайных величин.
- •5. Характеристики формы распределения.
- •4.3. Числовые характеристики меры связи случайных величин.
- •1. Ковариация.
- •2. Корреляция.
- •4.4. Распределения дискретных случайных величин.
- •1. Равномерное распределение.
- •2. Геометрическое распределение.
- •4. Биномиальное распределение.
- •5. Распределение Пуассона.
- •Примеры решения задач
- •Глава 5. Непрерывные случайные величины.
- •5.1. Функция распределения случайной величины
- •5.2. Плотность распределения вероятностей.
- •Связь между функцией распределения и плотностью распределения вероятностей.
- •5.3. Числовые характеристики непрерывных случайных величин
- •Примеры решения задач
- •Глава 6. Распределения непрерывных случайных величин
- •6.1. Равномерное распределение.
- •6.2. Показательное (экспоненциальное) распределение.
- •6.3. Нормальное распределение
- •Примеры решения задач
2. Геометрическое распределение.
Случайная величина Х имеет геометрическое распределение, если
![]() ,
k=0,1,2,…,
0<p<1,
q=1-p (4.26)
,
k=0,1,2,…,
0<p<1,
q=1-p (4.26)
Геометрическое распределение имеет случайная величина Х, равная числу испытаний до первого успеха с вероятностью успеха в единичном испытании р.
Математическое
ожидание геометрического распределения
![]() .
.
Дисперсия
дискретной случайной величины,
распределенной по геометрическому
закону равна
![]() .
.
Стандартное
отклонение
![]() .
.
4. Биномиальное распределение.
Целочисленная
случайная величина Х, принимающая
значения от 0 до n,
имеет биномиальное распределение, если
![]() задаются формулой Бернулли.
задаются формулой Бернулли.
-
Х
0
k
n
Р
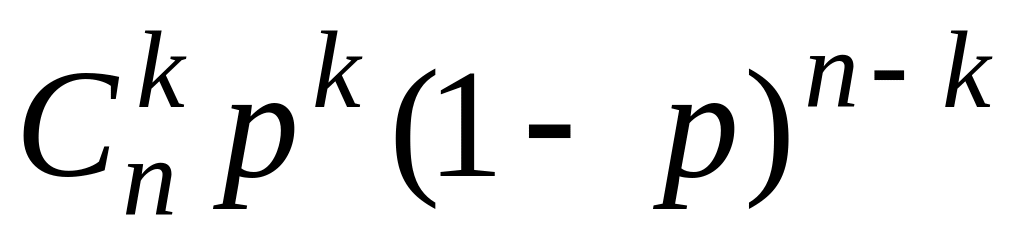
.
Математическое
ожидание биномиального распределения
![]() .
.
Дисперсия
дискретной случайной величины,
распределенной по биномиальному закону
равна
![]() .
.
Стандартное
отклонение
![]() .
.
5. Распределение Пуассона.
При
больших значениях n
вычисление вероятностей
![]() по формуле Бернулли становится
затруднительным. Если
по формуле Бернулли становится
затруднительным. Если
![]() формулу Бернулли заменяют приближенной
асимптотической формулой Пуассона.
формулу Бернулли заменяют приближенной
асимптотической формулой Пуассона.
![]() (4.27)
(4.27)
Математическое
ожидание распределения Пуассона:
![]() .
.
Дисперсия
дискретной случайной величины,
распределенной по закону Пуассона равна
![]() .
.
Стандартное
отклонение
![]() .
.
Примеры решения задач
4.1. Найти математическое ожидание дискретной случайной величины X, заданной законом распределения:
а) Х –4 6 10 . б) X 0,21 0,54 0,61
р 0,2 0,3 0,5 р 0,1 0,5 0,4.
Решение: а) Математическое ожидание равно сумме произведений всех возможных значений Х на их вероятности:
М(Х)=-4 . 0,2 +6 . 0,3+10 . 0,5=6.
4.2. Найти математическое ожидание и дисперсию случайной величины Z, если известны математические ожидания и дисперсии Х и Y: Z=X-2Y, M(X)=5, M(Y)=3, D(X)=2, D(Y)=4.
Решение: Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых, постоянный множитель можно вынести за знак математического ожидания), получим
М (Z)= М (X -2Y) = М (X) - М (2Y) = М (X) - 2M(Y) = =5-2.3=-1.
Используя свойства дисперсии (дисперсия разности независимых случайных величин равна сумме дисперсий слагаемых, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат), получим
D(Z)=D(X-2Y)=D(X)+4D(Y)=2+4.4=18.
4.3. Охранное устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Возможные значения случайной величины Х={0,1,2,3}. Отказы элементов независимы один от другого, вероятности отказа каждого элемента равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, n=3, p=0,1, следовательно q=1-p=0,9, получим:
![]()
Контроль: 0,729+0,243+0,027+0,001=1.
Напишем биномиальный закон распределения:
Х |
0 |
1 |
2 |
3 |
р |
0,729 |
0,243 |
0,027 |
0,001 |
4.4. Учебник по теории вероятностей издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Составить первые 3 члена закона распределения дискретной случайной величины Х – числа бракованных книг в тираже.
Решение: Возможные значения Х равны {0, 1, 2, 3, …, k}. События, состоящие в том, что книги сброшюрованы неправильно, независимы, число n велико, а вероятность р мала, поэтому воспользуемся распределением Пуассона (4.32):
![]()
По
условию, n=100000,
p=0,0001,
следовательно,
q=0,9999
(npq=9,999).
Найдем
![]() .
Вероятности возможных значений будут
равны:
.
Вероятности возможных значений будут
равны:
![]()
Закон распределения запишется в следующем виде:
Х |
0 |
1 |
2 |
… |
р |
0,000045 |
0,00045 |
0,00225 |
… |
4.5. Производится 3 выстрела с вероятностями попадания в цель, равными р1=0,4; р2=0,3 и р3=0,6. Найти математическое ожидание общего числа попаданий.
Решение: Число попаданий при одном выстреле есть случайная величина Х1, возможные значения которой 1 (попадание) с вероятностью р1=0,4 и 0 (промах) с вероятностью q1=1-0,4=0,6. Математическое ожидание М(Х1)=0,4. Аналогично найдем математические ожидания М(Х2)=0,3 и М(Х3)=0,6.
Общее число попаданий есть также случайная величина, состоящая из суммы попаданий в каждом из трех выстрелов: Х=Х1+Х2+Х3. Тогда математическое ожидание общего числа попаданий равно
М(Х)=М(Х1+Х2+Х3 )=М(Х1)+М(Х2)+М(Х3)=0,4+0,3+0,6=1,3 (попаданий).
4.6. Дискретная случайная величина Х задана законом распределения:
Х 1 2 4
р 0,1 0,3 0,6
Найти центральные моменты первого, второго, третьего и четвертого порядков.
Решение:
Центральный момент первого порядка
равен нулю
![]() =0.
=0.
Для вычисления центральных моментов удобно воспользоваться формулами, выражающими центральные моменты через начальные, поэтому предварительно найдем начальные моменты
1=М(Х) =1 . 0,1+ 2 . 0,3- 4 . 0,6=3,1.
2=M(X2)=1 . 0,1+ 4 . 0.3+ 16 . 0,6=10,9;
3=М(XЗ)=l . 0,1+ 8 . 0,3+64 . 0,6=40,9;
4=M(X4)=1 . 0,1 +16 . 0,3+256 . 0,6=158,5.
Найдем центральные моменты.
![]() =10,9
- 3,12=
1,29;
=10,9
- 3,12=
1,29;
![]() =
40,9 – 3 .
3,1 .
10,9 +2 .
3,13=
-0,888;
=
40,9 – 3 .
3,1 .
10,9 +2 .
3,13=
-0,888;
![]() =
=
=158,5 – 4 . 40,9 . 3,1+6 . 10,9 . 3,12 – 3 . 3,14=2,7777.
