Глава 5. Непрерывные случайные величины.

Случайная величина, значения которой заполняют некоторый промежуток, называется непрерывной.

5.1. Функция распределения случайной величины

Способы задания дискретной случайной величины неприменимы для непрерывной. В этой связи вводится понятие функции распределения вероятностей.

Функцией распределения называют функцию , определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т.е.

. (5.1)

Функция распределения дискретной случайной величин, принимающей значения с вероятностями , определяется следующим образом:

. (5.2)

Свойства функции распределения:

1. Значения функции распределения принадлежат отрезку [0,1].

2. Функция распределения есть неубывающая функция: 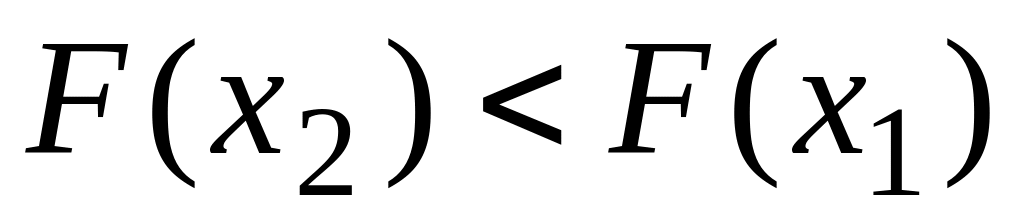если .

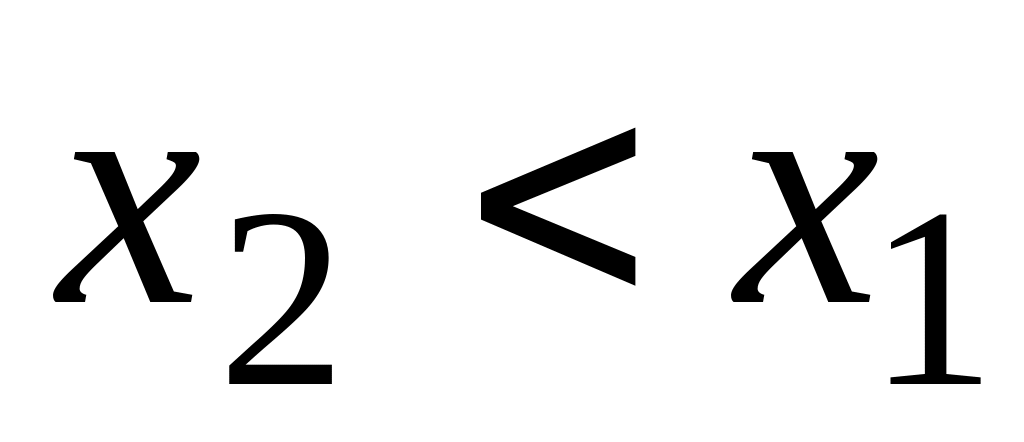3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале , равна приращению функции распределения на этом интервале:

. (5.3)

Следствие: Вероятность того, что случайная величина примет одно значение равно нулю.

4. Если все возможные значения случайной величины Х принадлежат интервалу (a,b), то

при и при

Следствие: Справедливы следующие предельные соотношения:

, (5.4)

5. Вероятность того, что случайная величина Х примет значение большее, чем х равно разности между единицей и функцией распределения:

.

5.2. Плотность распределения вероятностей.

Плотностью распределения вероятностей f(х) непрерывной случайной величины Х называется предел, если он существует, отношения вероятности попадания случайной величины Х в интервал (х; х + х), примыкающий к точке х, к длине этого интервала, когда последняя стремится к нулю.

Свойства плотности распределения:

1. f(x) – неотрицательная функция, т.к. предел неотрицательных величин есть функция неотрицательная.

2. Вероятность попадания непрерывной случайной величины Х  на промежуток [а; b] равна сумме элементов вероятности на всем этом отрезке, т.е. определённому интегралу по промежутку [a;b] от плотности распределения вероятностей:

P(a  Х  b) =  (5.5)

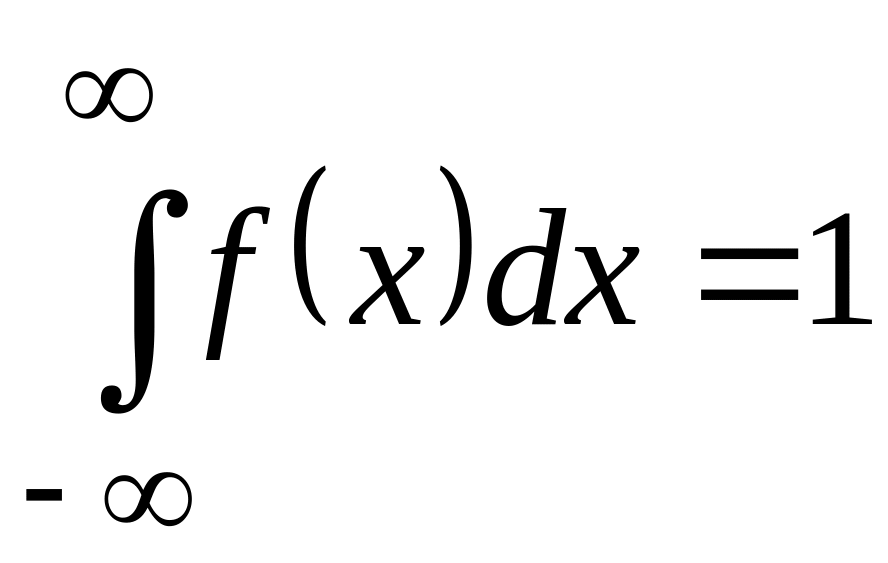3. , т.к. вероятность того, что случайная величина примет значения из интервала 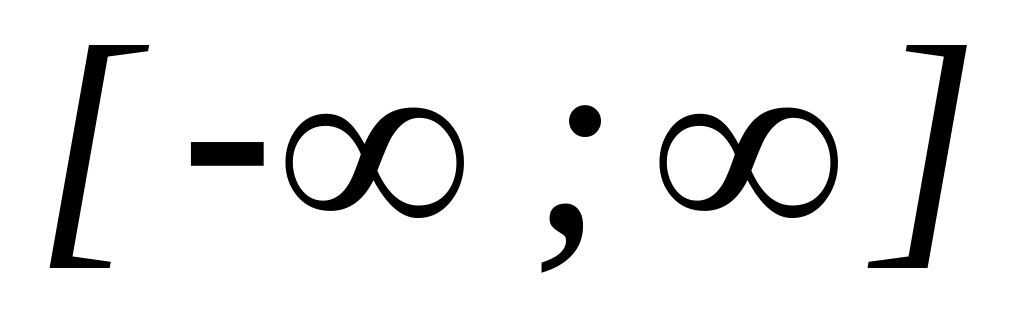, т.е. вероятность достоверного события равна 1.

Если все возможные значения случайной величины принадлежат интервалу (а; b), то для f(х) – её плотности распре­деления справедливо равенство

Плотностью распределения может служить любая интегрируемая функция f(х), удовлетворяющая двум условиям:

1. f(х)  0;

2. 

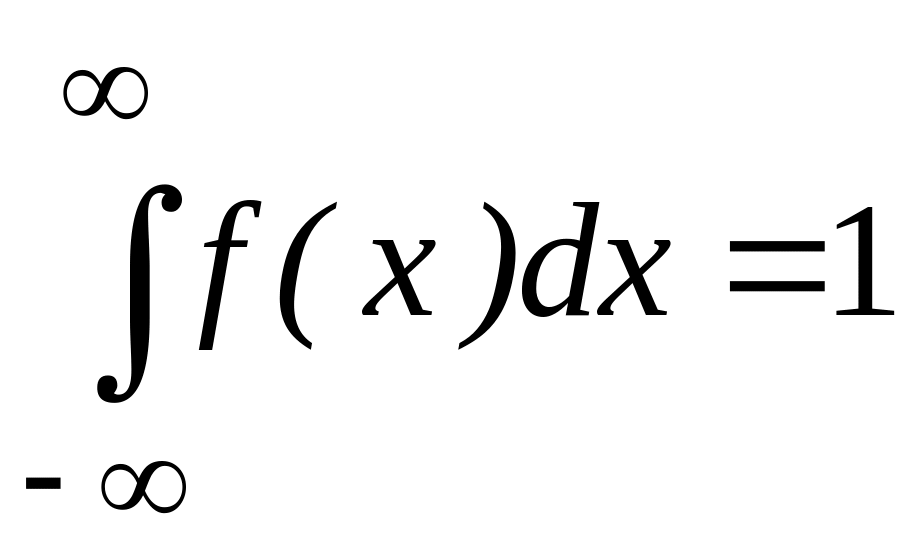
Связь между функцией распределения и плотностью распределения вероятностей.

Функция F(x), которая определяется равенством , называется интегральной функцией распределения или просто функцией распределения случайной величины Х. Непосредственно из определения следует равенство

. (5.6)

Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению . Плотность распределения f(х) называют дифференциальной функцией распределения.

5.3. Числовые характеристики непрерывных случайных величин

1. Математическое ожидание. Математическим ожиданием М(Х) (или МХ) случайной величины Х, возможные значения которой принадлежат всей числовой оси, называется несобственный интеграл

. (5.7а)

Если возможные значения принадлежат отрезку [a;b], то математическое ожидание есть определенный интеграл:

(5.7б)

2. Дисперсия случайной величины. Дисперсия случайной величины D(Х) – это математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

D(Х) = M(Х – M( Х))² (5.8)

Часто для нахождения дисперсии используется формула:

D(X)=  (5.9)

Если возможные значения принадлежат отрезку [a;b], то дисперсия будет равна определенному интегралу по промежутку [a;b]:

(5.10)

3. Среднее квадратическое (стандартное) отклонение. Средним квадратическим отклонением случайной величины X называется арифметический корень из дисперсии:

4. Моменты случайных величин. Начальным теоретическим моментом k-ой порядка называют математическое ожидание случайной величины :

(5.11)

Центральным теоретическим моментом k-го порядка называется математическое ожидание k-ой степени отклонения :

(5.12)

Если распределение вероятностей случайной величины симметрично относительно её математического ожидания, то все центральные моменты нечетного порядка равны нулю: .

6. Характеристики формы распределения. Коэффициентом асимметрии случайной величины Х называется число , равное отношению третьего центрального момента к кубу среднеквадратического отклонения случайной величины Х:

(5.13)

Эксцессом случайной величины X называется число , равное разности отношения четвертого центрального момента к четвертой степени среднего квадратического отклонения случайной величины и числа 3:

(5.14)