6.3. Нормальное распределение

Нормальный закон распределения получен в связи с разработкой теории ошибок наблюдения. Случайные ошибки складываются из множества различных неконтролируемых причин: температурных колебаний, вибраций в окружающей среде, неточности измерительной шкалы прибора и т. д. Если каждая из этих случайных причин оказывает на результаты измерений незначительное влияние по сравнению с общим эффектом, то их сумма (случайная ошибка) подчинена закону, близкому к нормальному (для появления нормального распределения необходимо выполнение дополнительных условий). Например, рост большого числа лиц одного и того же пола, национальности и возраста, размеры органов животных также подчиняются нормальному распределению.

Н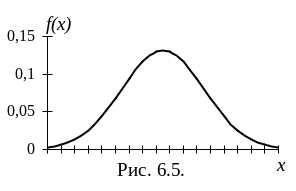 епрерывная случайная величина имеет нормальное распределение вероятностей с параметрами а и  >0, если её плотность распределения вероятностей имеет вид:

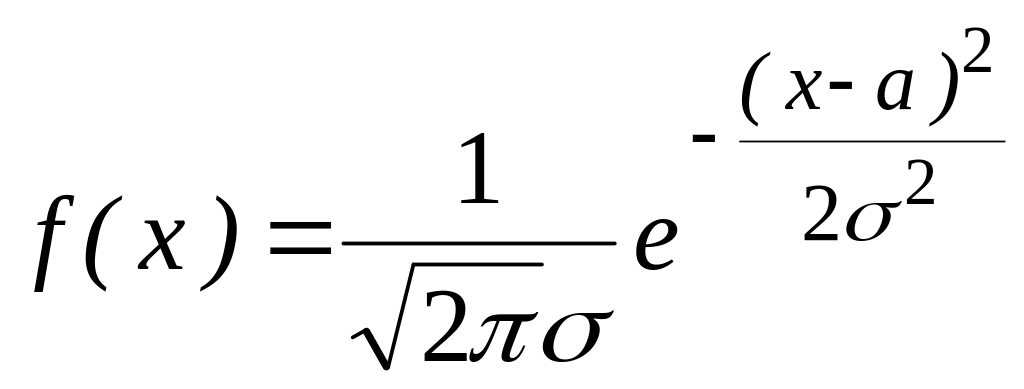(6.7)

Кривая распределения – это кривая Гаусса, которая имеет симметричный колоколообразный вид (рис. 6.5). Из формулы (6.7) следует, что кривая f(x) достигает максимум в точке ( ) и имеет две точки перегиба ( ) Плотность распределения f(x) симметрична относительно прямой , т.е. f(a+y)=f(a-y). Если , то .

Функция распределения F(x) нормально распределенной случайной величины Х имеет вид:

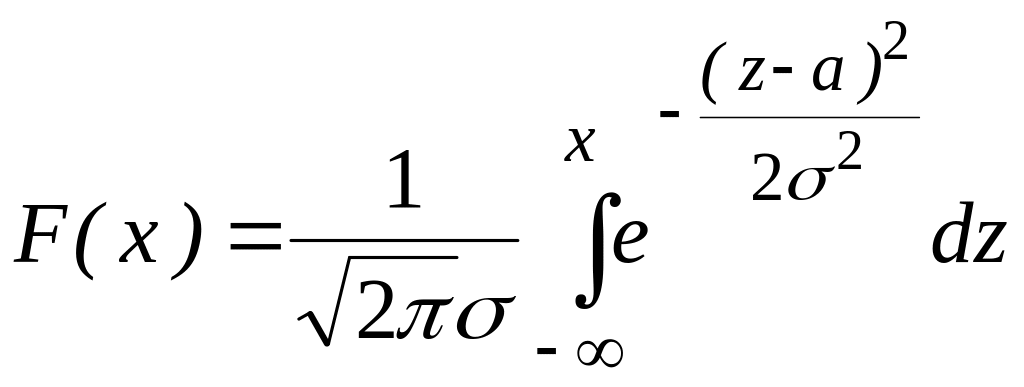(6.8)

Полученный интеграл нельзя выразить через элементарные функции, но его можно вычислить через специальную функцию:

,

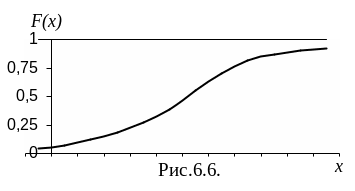
называемую нормированной функцией нормального распределения с параметрами а=0 и =1 или через функцию Лапласа:

.

Значения функции Лапласа приведены в Приложении. Её график изображен на рисунке 6.6.

Математическое ожидание нормально распределенной случайной величины равны . Дисперсия – , стандартное отклонение . Коэффициент асимметрии и эксцесс равны нулю.

Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный интервал определяется с помощью нормированной функции нормального распределения по формуле:

, (6.10)

где .

Вероятность того, что отклонение нормально распределенной случайной величины Х по абсолютной величине меньше заданного положительного числа  равна:

(6.11)

Из полученных формул следует, что чем меньше , тем больше вероятность принять значение, принадлежащее интервалу .

Правило 3-х  (трех “сигм”). Пусть имеется нормально распределённая случайная величина Х с математическим ожиданием, равным а и дисперсией ². Определим веро­ятность того, что Х принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.

P(а – 3< Х < а + 3)=Ф(3) – Ф(–3)=2Ф(3) (6.12)

Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3.

Нормальное распределение играет большую роль в теории вероятностей и ее применениях. Это связано с тем, чтов соответствии с центральной предельной теоремой теории вероятностей при выполнении определенных условий сумма большого числа случайных величин имеет “примерно” нормальное распределение.