
- •Содержание
- •1. Введение
- •Определение
- •2. Задача Коши – решение дифференциального уравнения, так что выполняется начальные условия
- •Определение
- •5. Линейные уравнения
- •6. Нахождение частного решения оу Метод Бернулли
- •7. Задачи
- •8. Уравнения в полных дифференциалах
- •Определение
- •14. Огибающее семейство кривых Определение
- •Теорема
- •Теорема
- •19. Решение неоднородных уравнений
- •Метод неопределенных коэффициентов
- •20. Метод неопределенных коэффициентов
- •21. Определитель системы - определитель Вронского
- •22. Линейные уравнения с переменными коэффициентами
- •23. Дискретные задачи. Задачи с дискретным временем. (Рекуррентные последовательности)
- •24. Гармонические колебания
- •25. Система линейных уравнений с постоянными коэффициентами
- •26. Сведение системы из n-уравнений к одному уравнению n-го порядка
- •27. Решение систем общего вида
- •28. Решение неоднородных систем
- •Метод неопределенных коэффициентов
- •Теорема о существовании единственности (тсе)
26. Сведение системы из n-уравнений к одному уравнению n-го порядка
![]()
Дифференцируем первое уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обратная задача:
![]()
Вводим вектор:
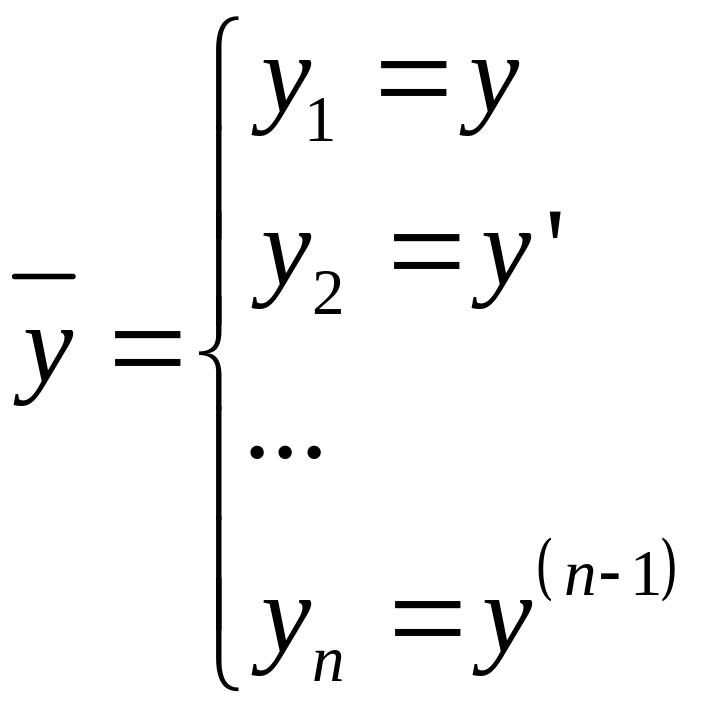
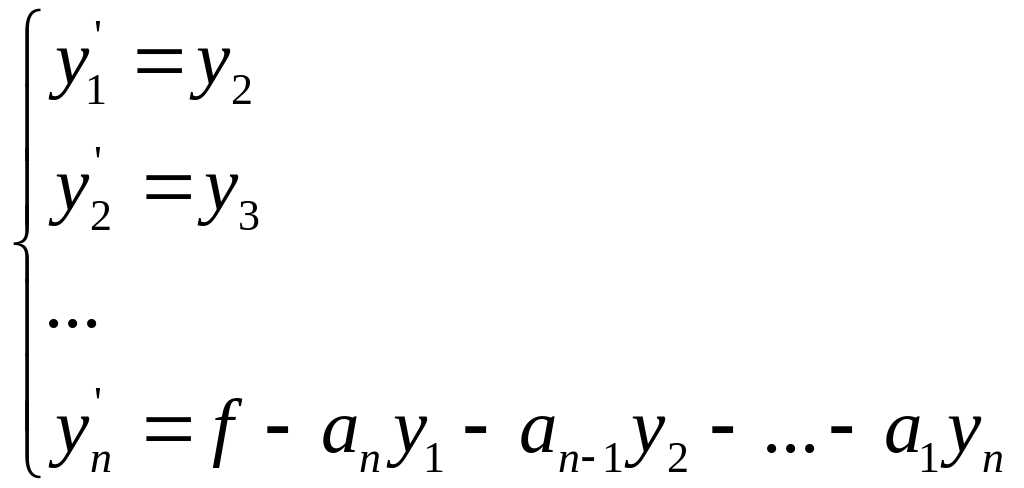
Матрица системы:
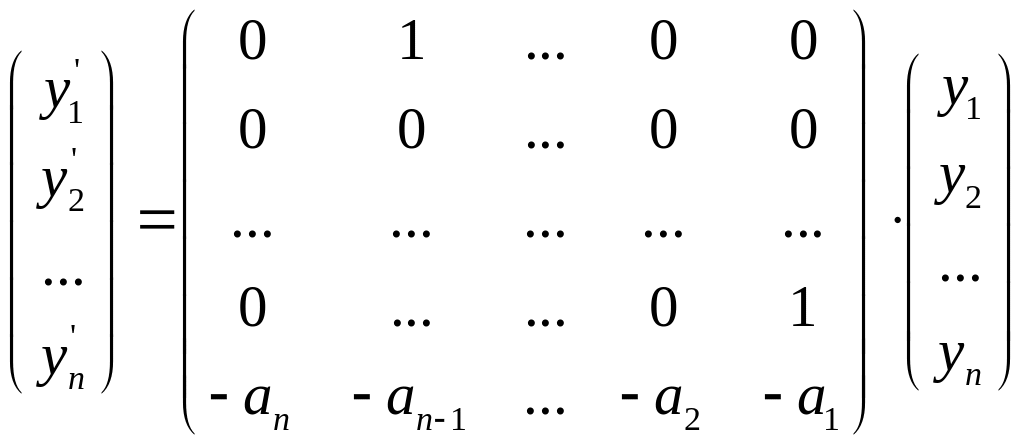
![]()
27. Решение систем общего вида
(матрицы, которые не приводятся к диагональному виду).
![]() найти
найти
![]()
![]()
![]() можно привести к
Жорданову виду.
можно привести к
Жорданову виду.
![]()
![]() -
Жорданова форма
-
Жорданова форма
 - Жордановы клетки
- Жордановы клетки
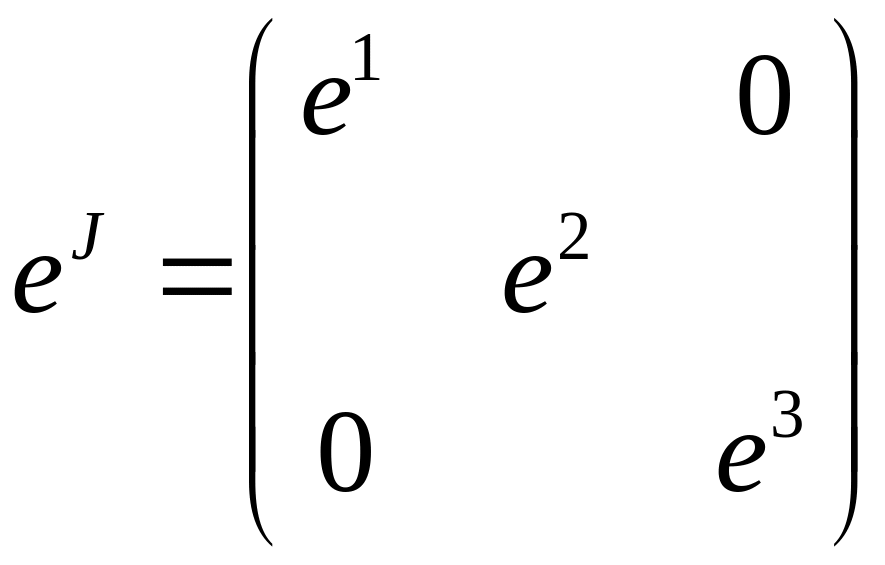
Надо уметь находить exp от Жордановой клетки.
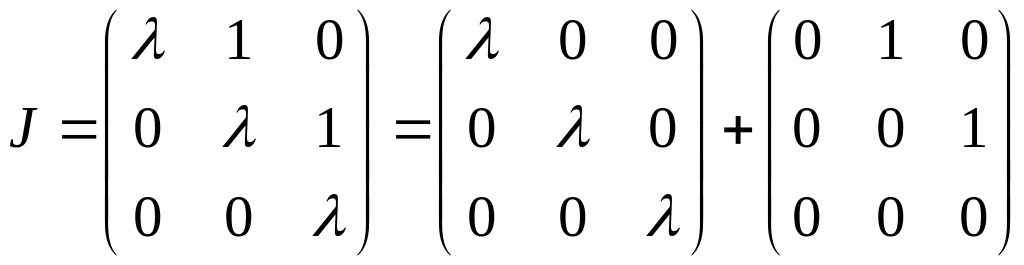
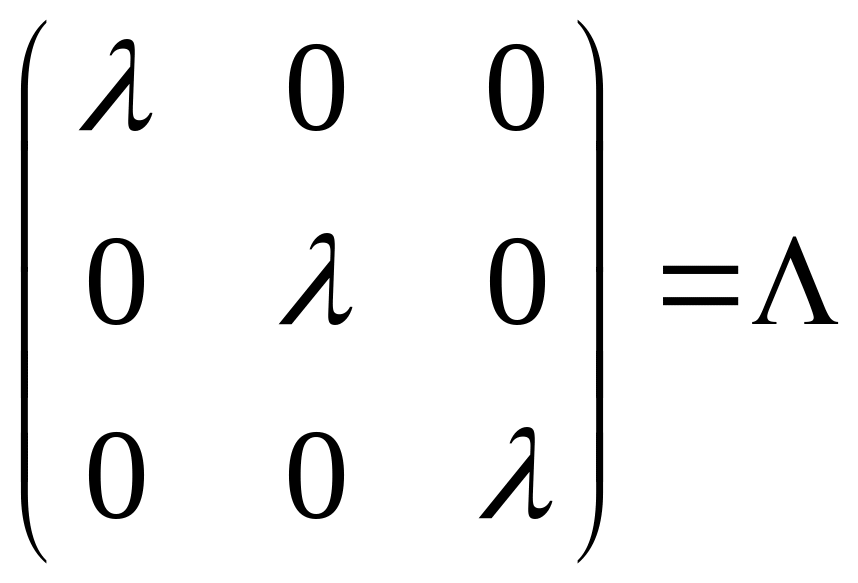
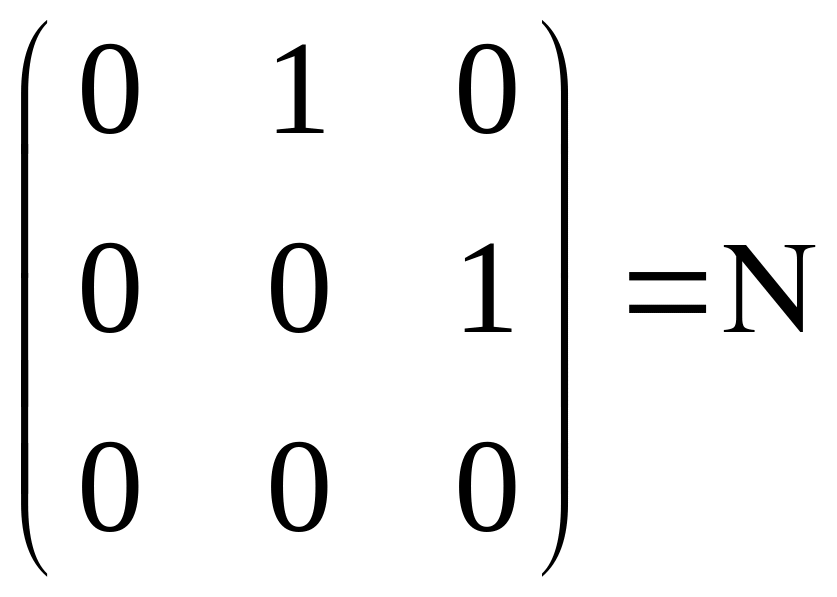
Лемма:
Если
![]() (матрицы А и В коммутируют), то
(матрицы А и В коммутируют), то
![]()
Доказательство:
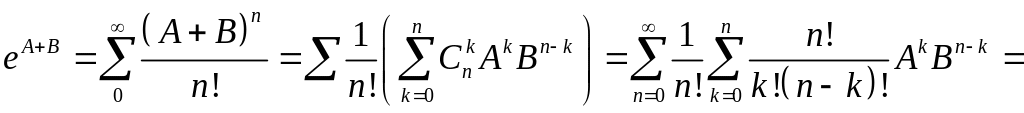
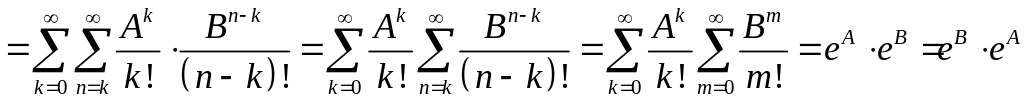 чтд.
чтд.
и
![]() коммутируют
коммутируют
![]()
![]() - диагональная
матрица,
- диагональная
матрица,
![]() -
нильпотентная
-
нильпотентная
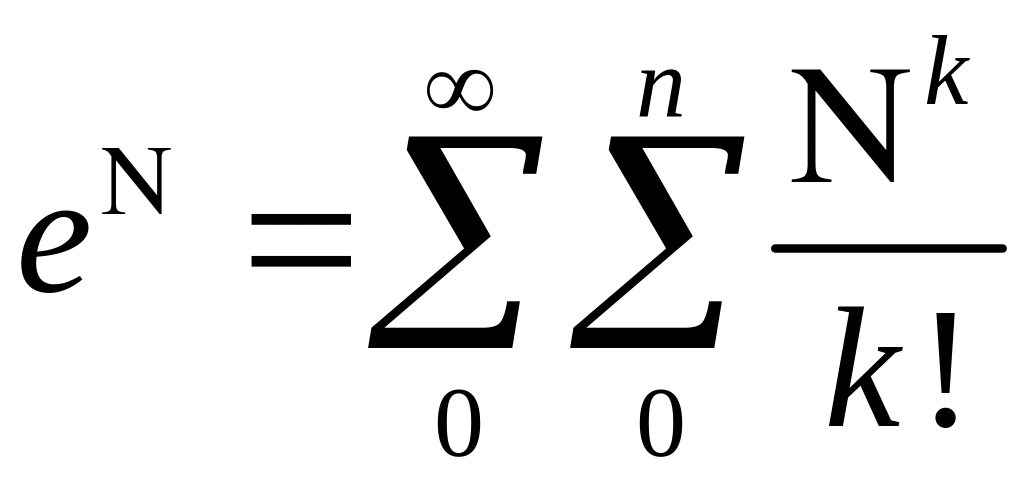
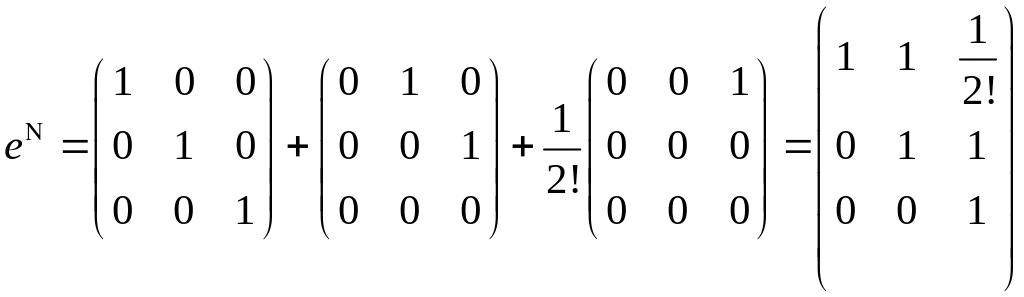
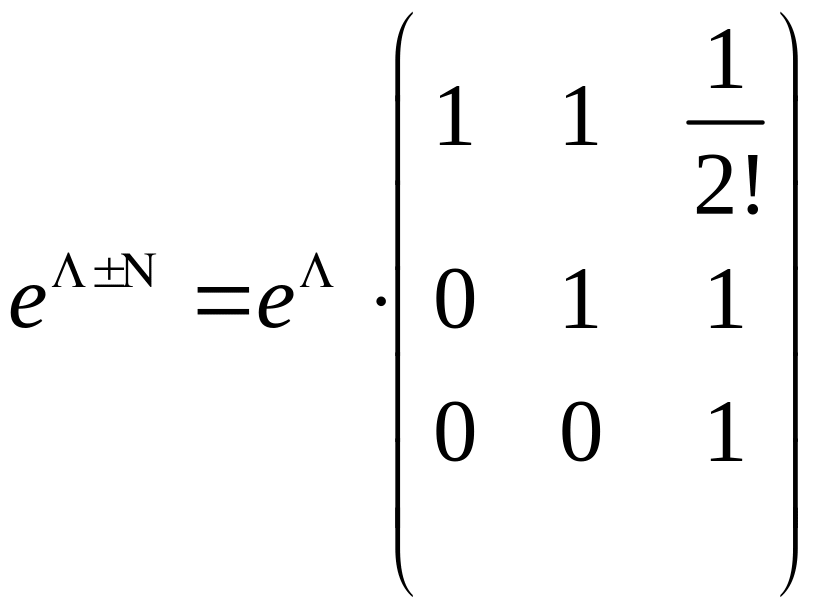
Проблема
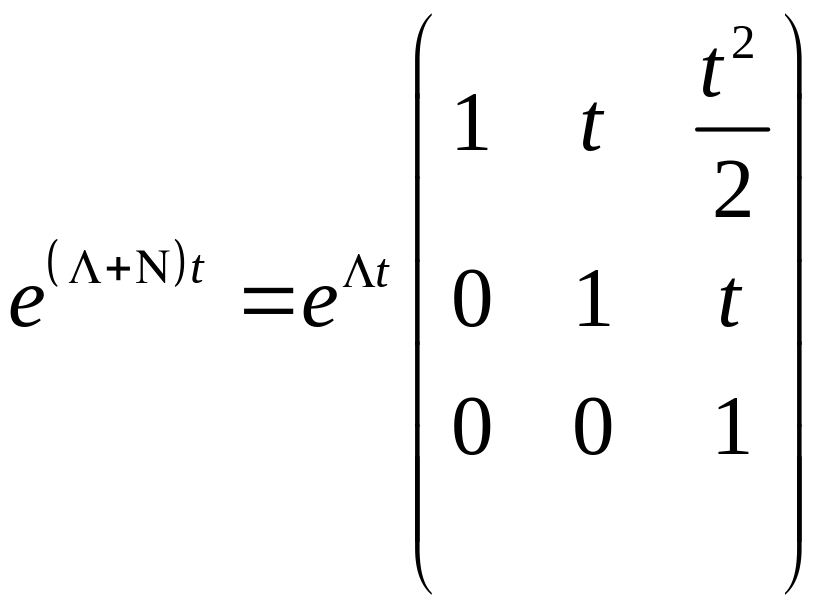
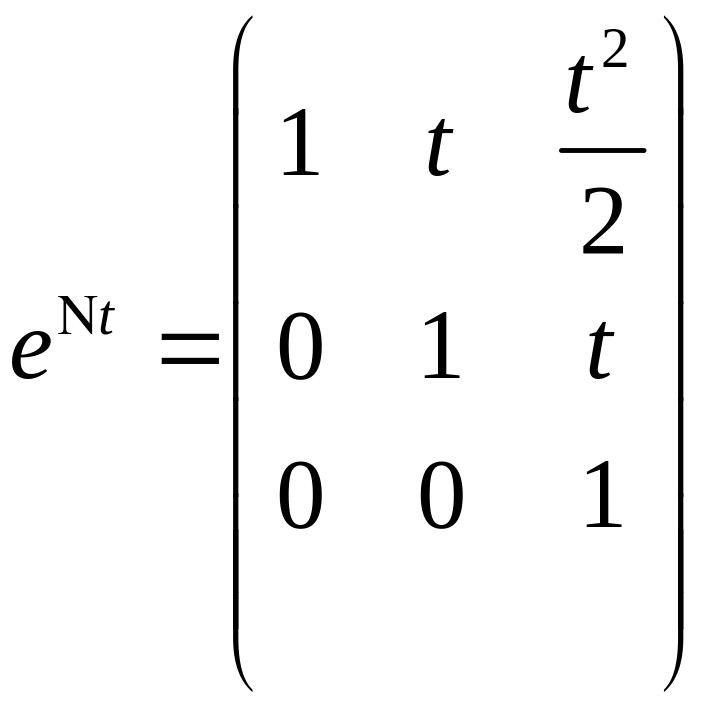
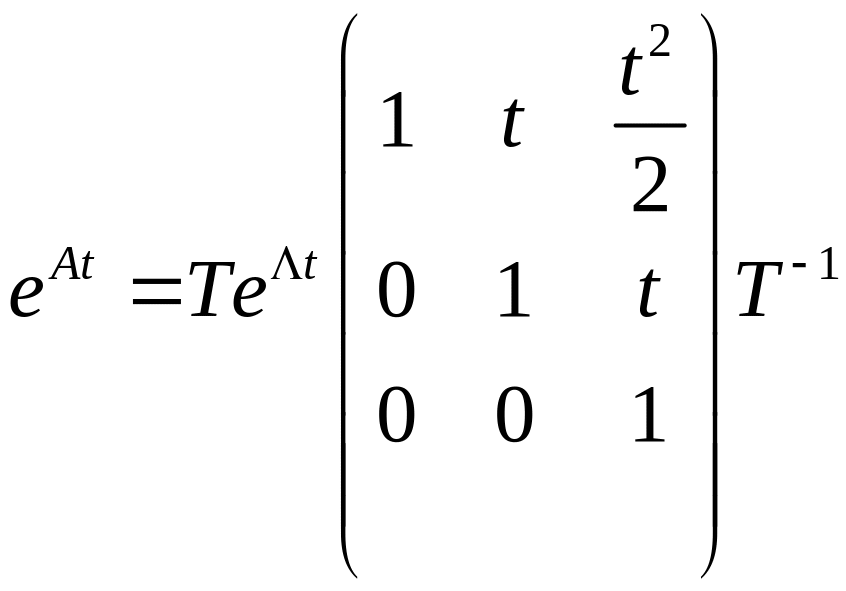
Т – матрица из собственных и присоединенных векторов.
Пример.
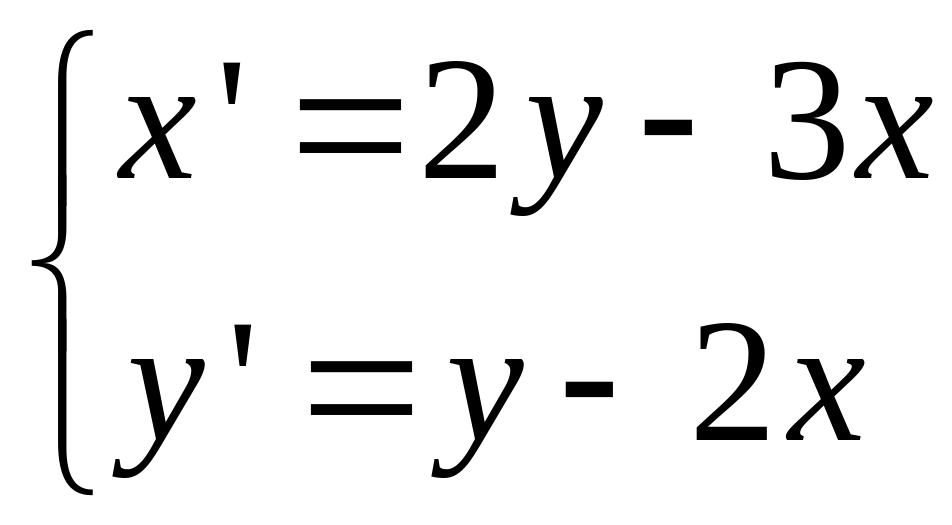
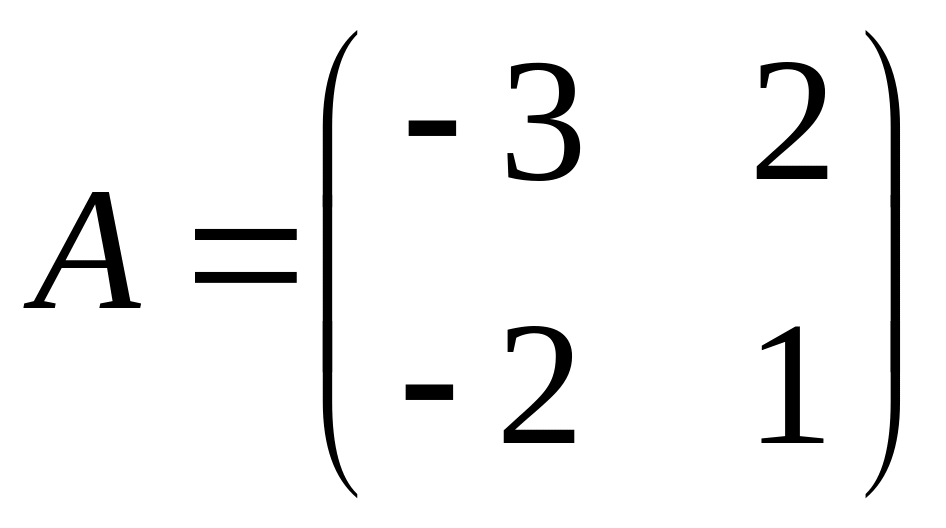
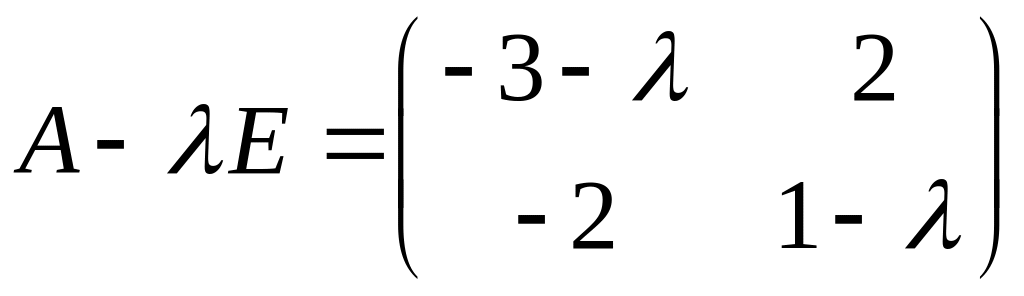
![]()
![]()
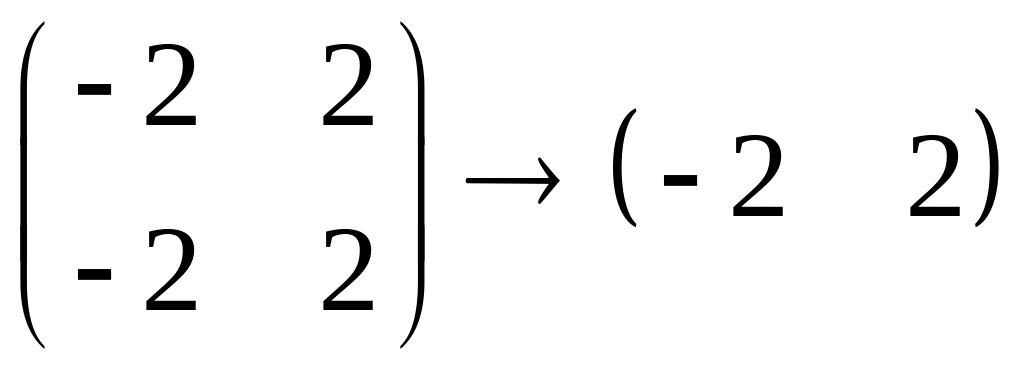
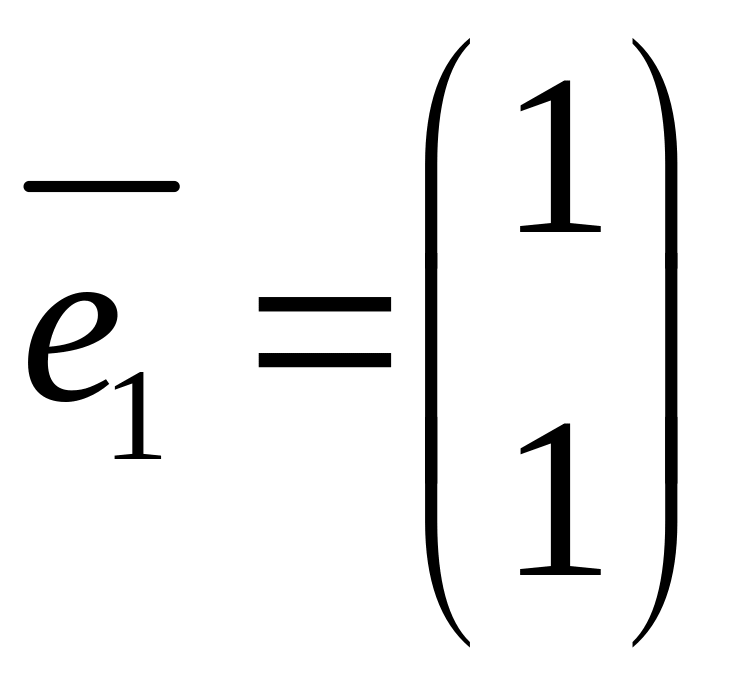 -
собственный
вектор
-
собственный
вектор
![]()
![]()
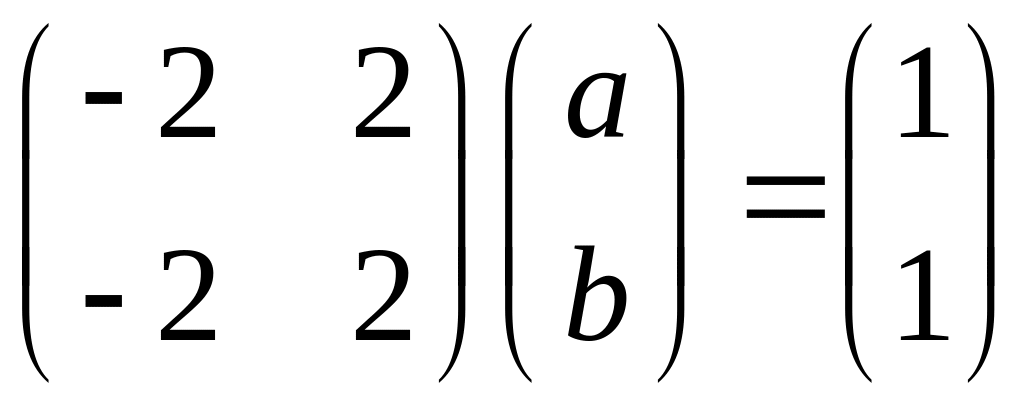
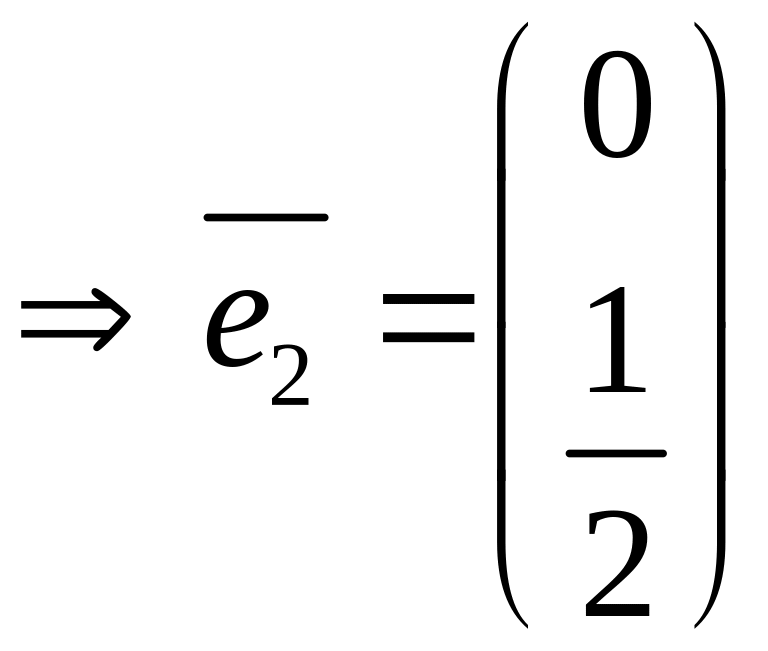
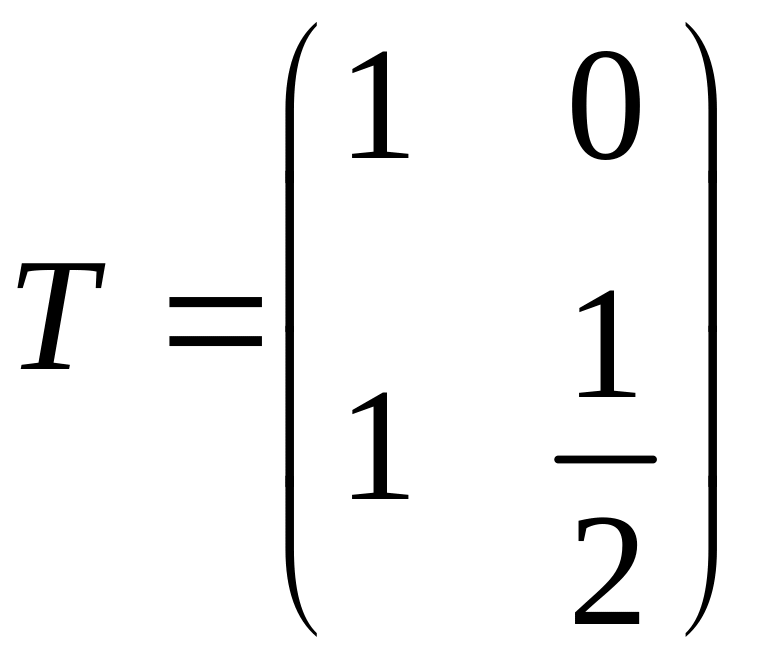
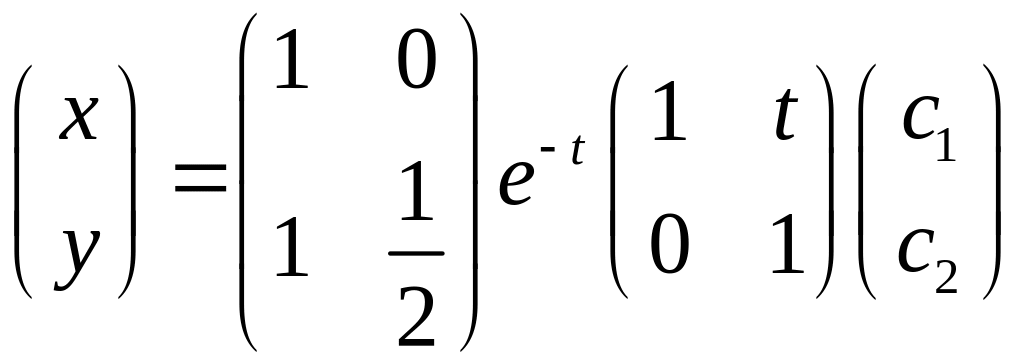
Пример
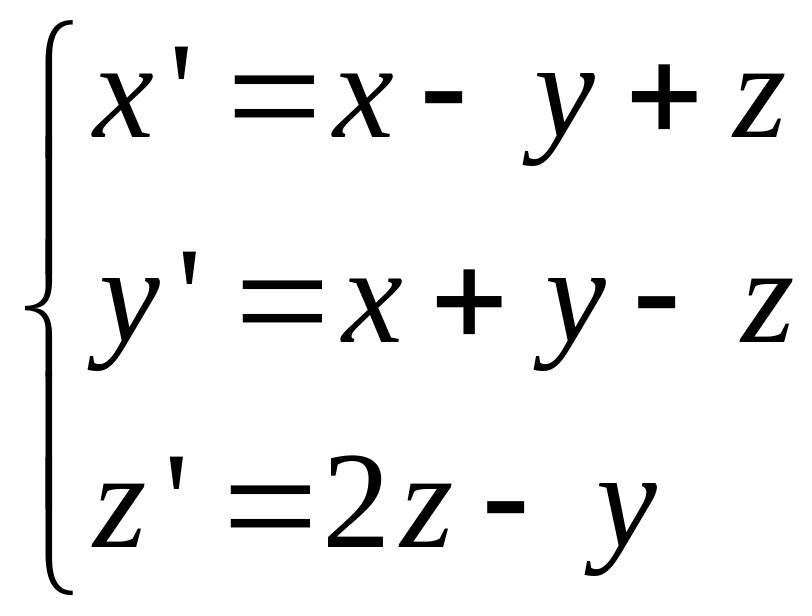
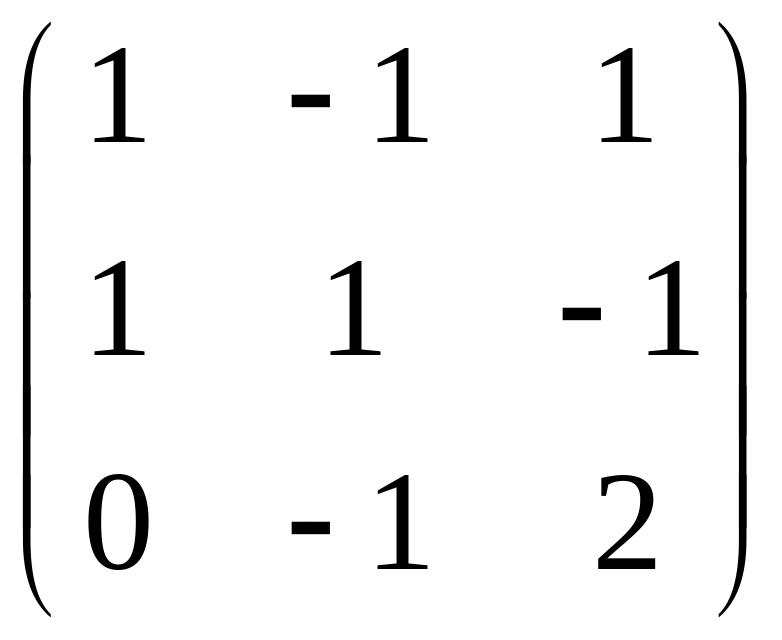
![]()
![]() 1
собственный вектор
1
собственный вектор

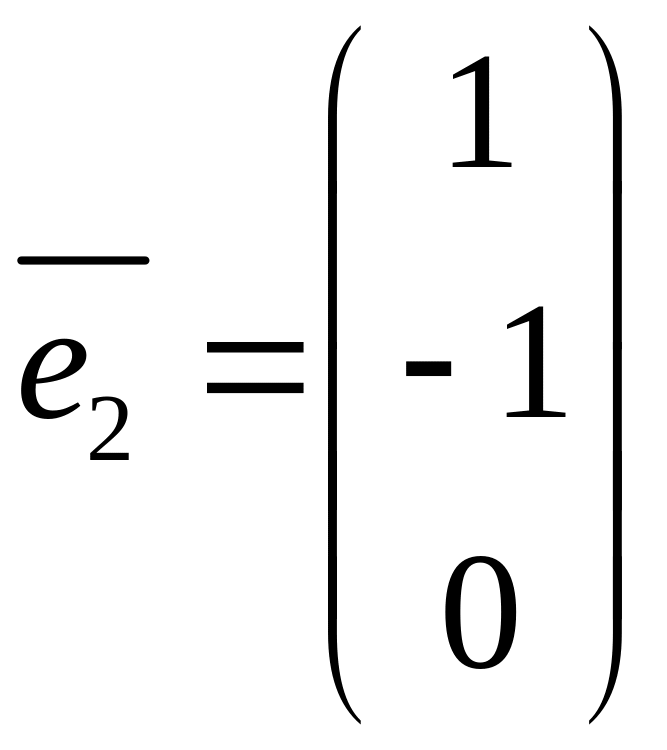
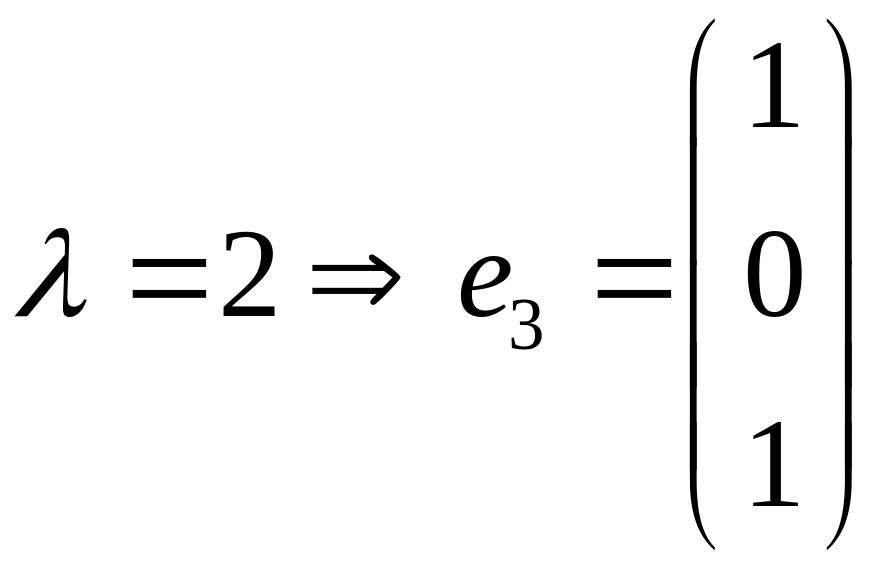

28. Решение неоднородных систем
Вариация произвольной постоянной
Метод неопределенных коэффициентов
Система
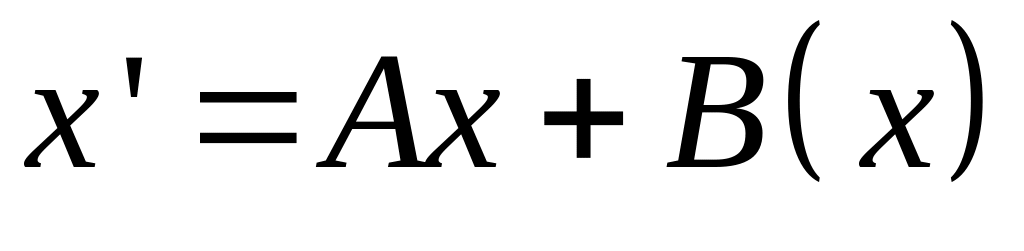
1. Решение однородной системы:
![]()
![]()
2. Решение неоднородной системы:
![]()
![]()
![]()
![]()
![]()
![]() - общее решение
- общее решение
Пример
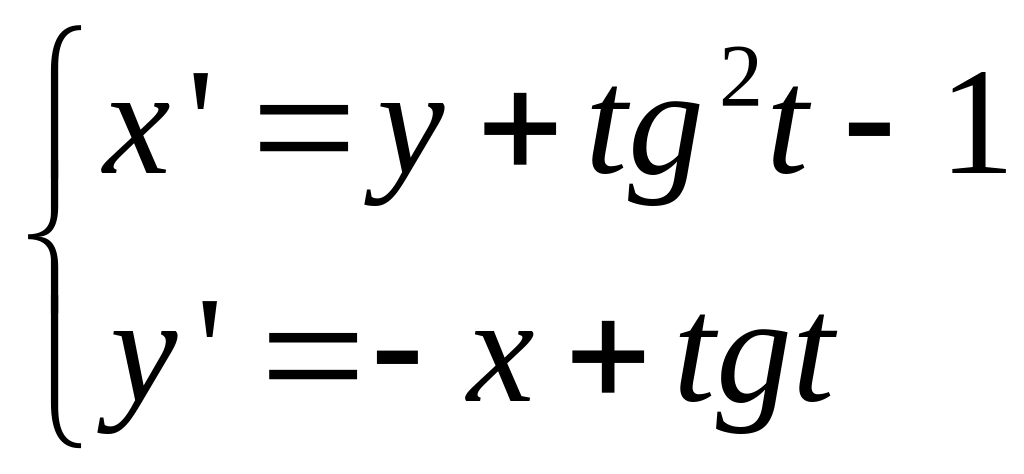
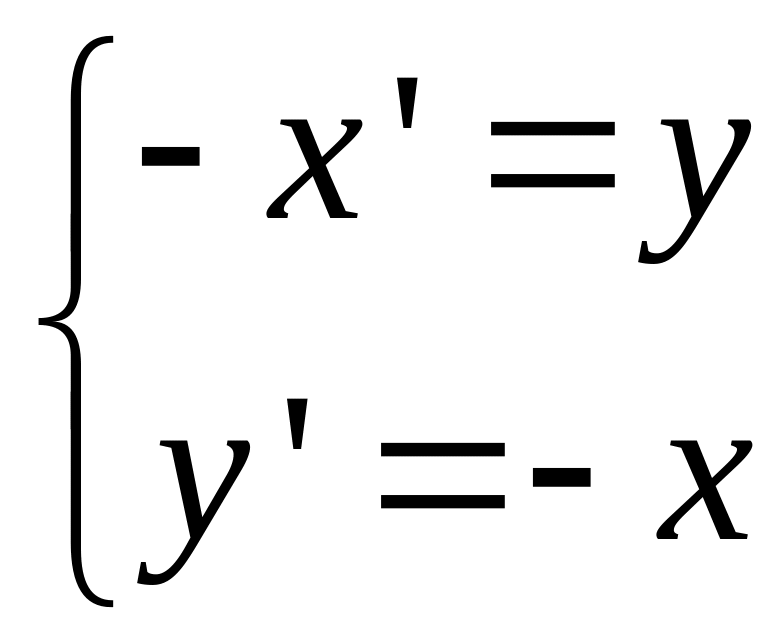
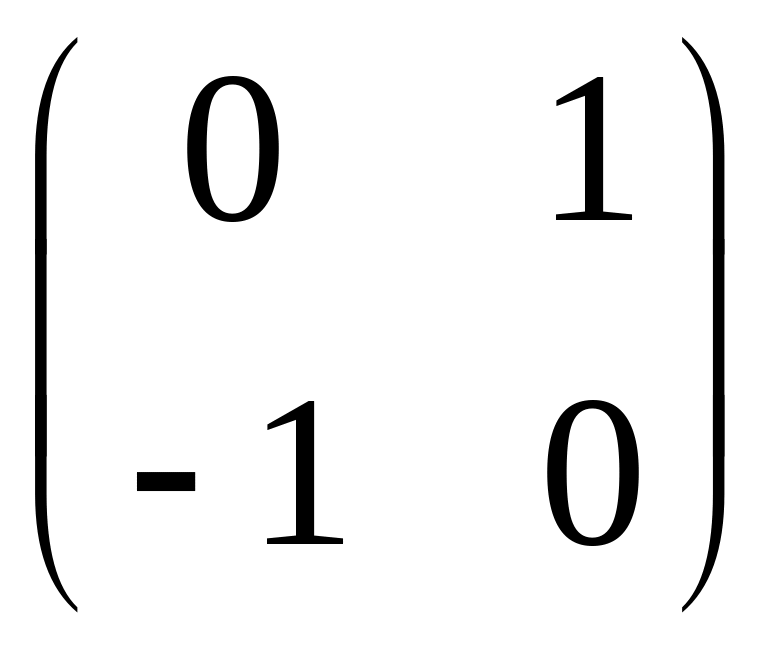
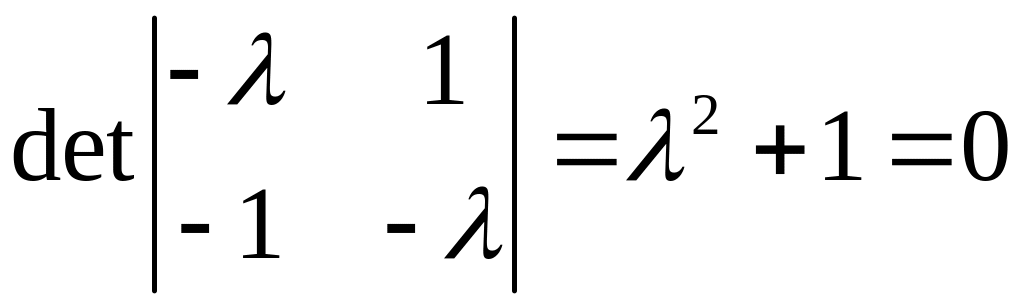
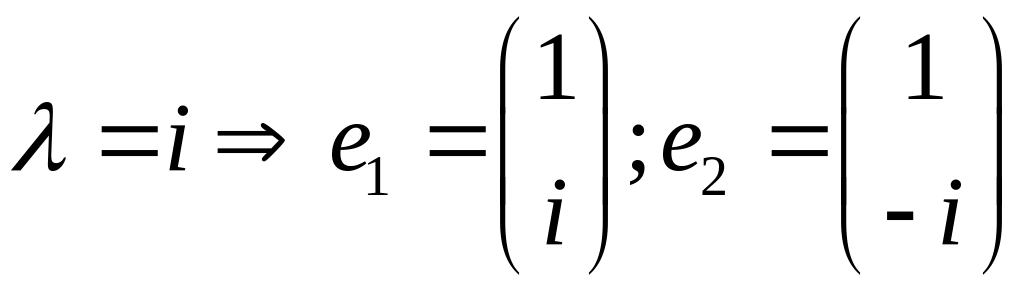
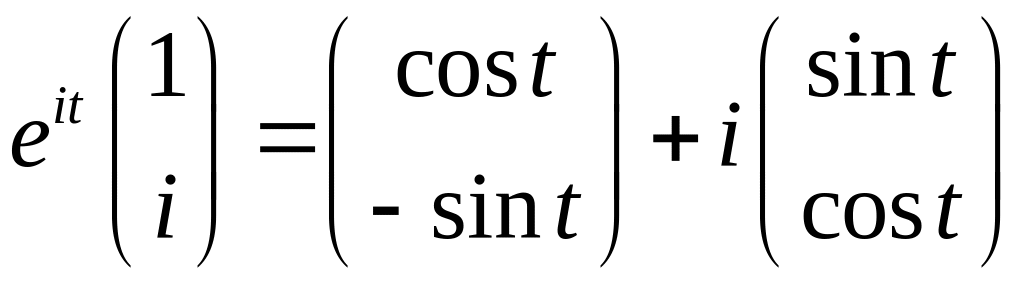
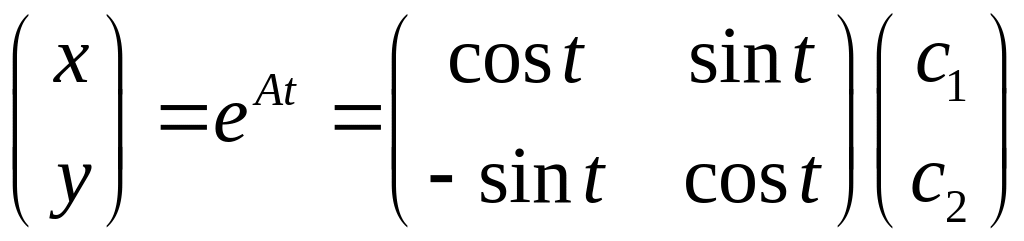
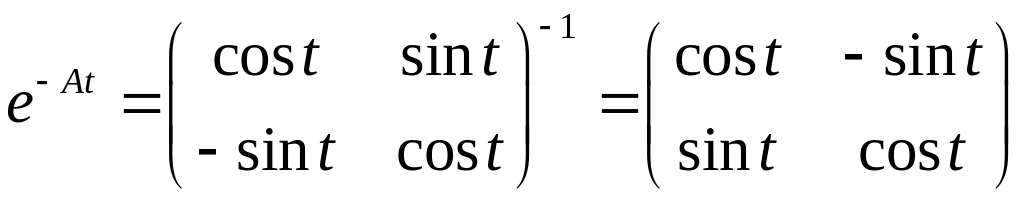
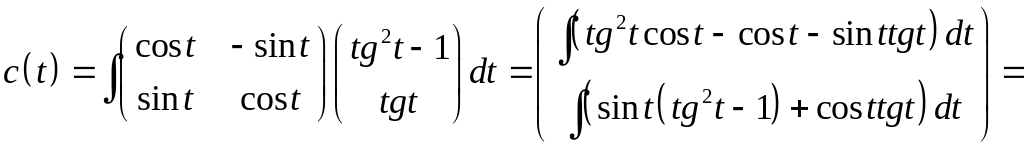
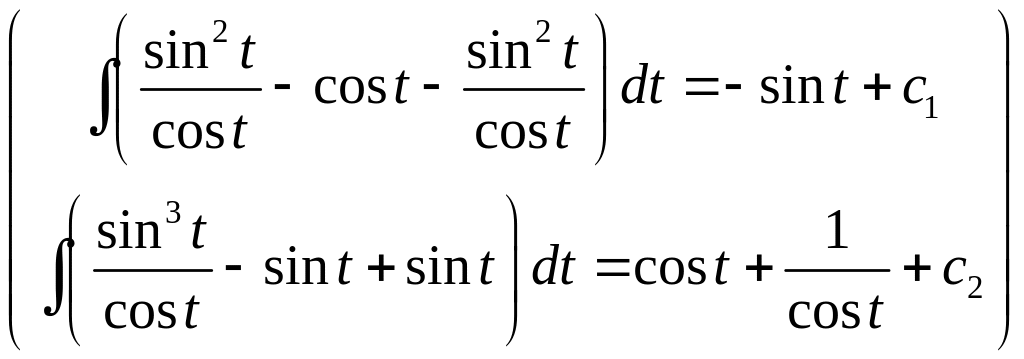
Ответ:
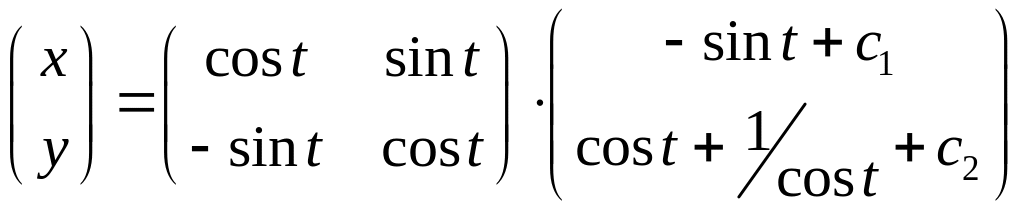
Пример
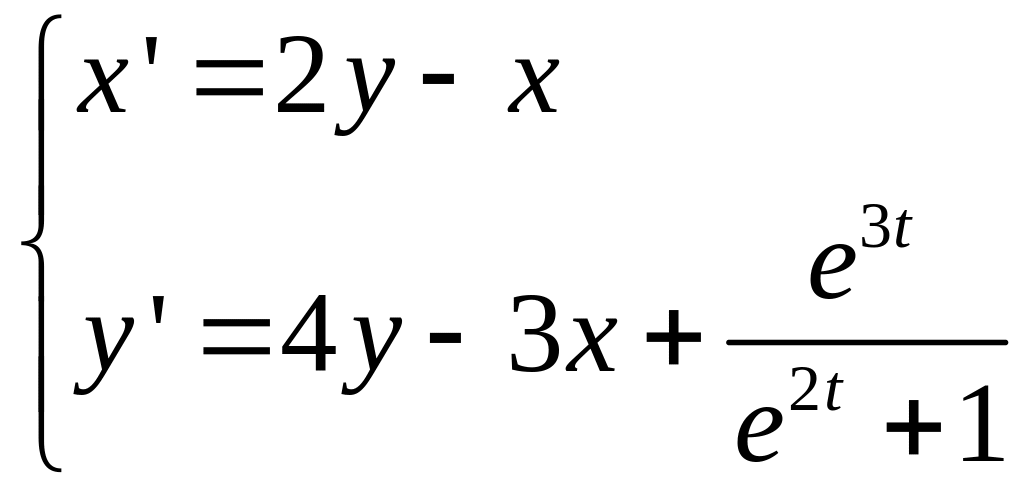
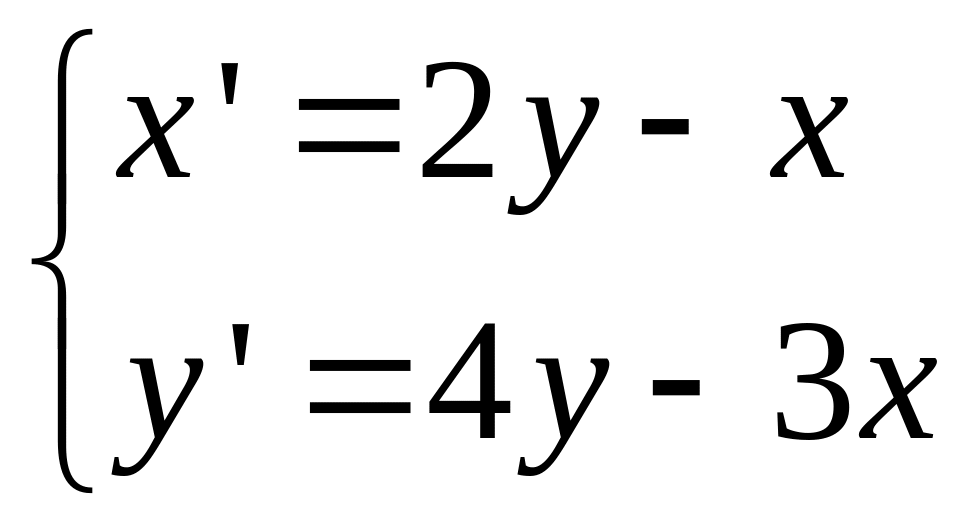
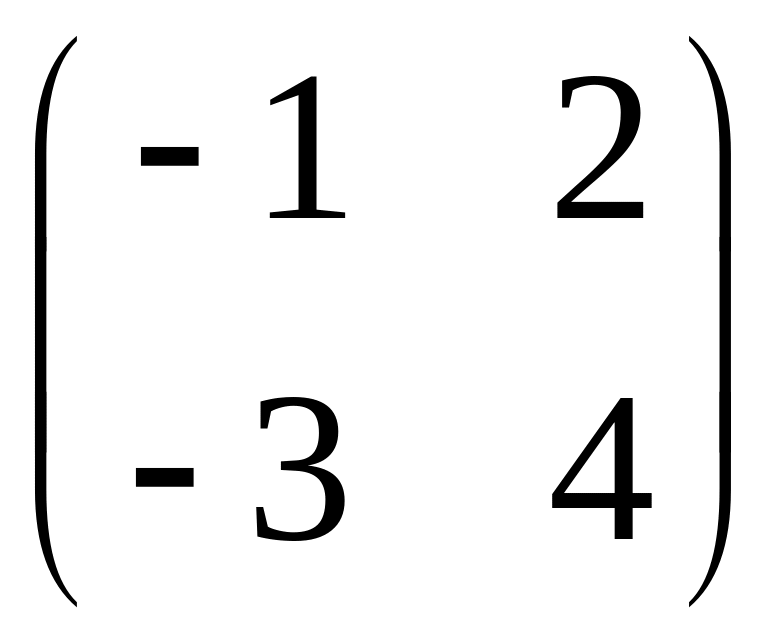
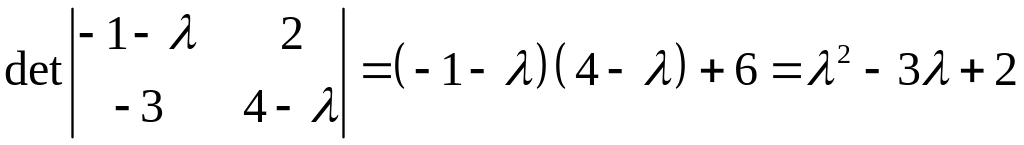
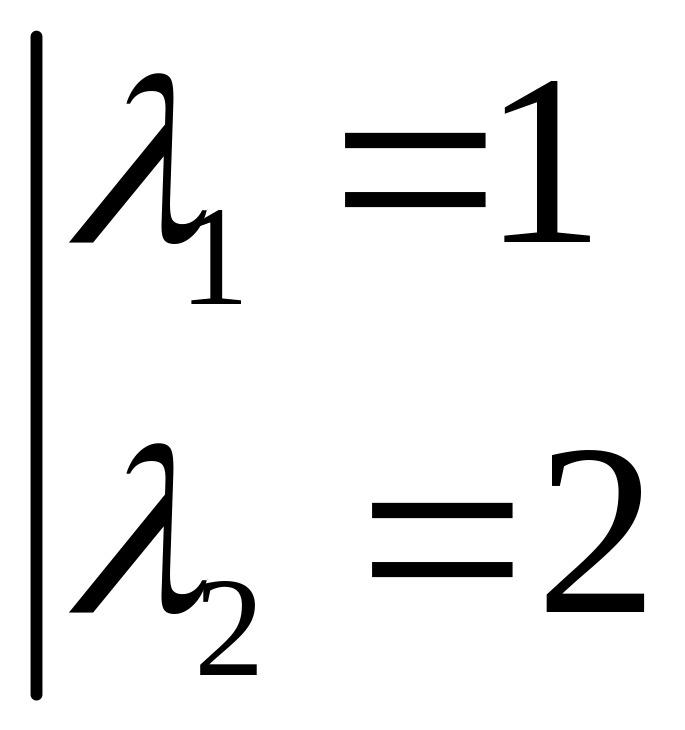
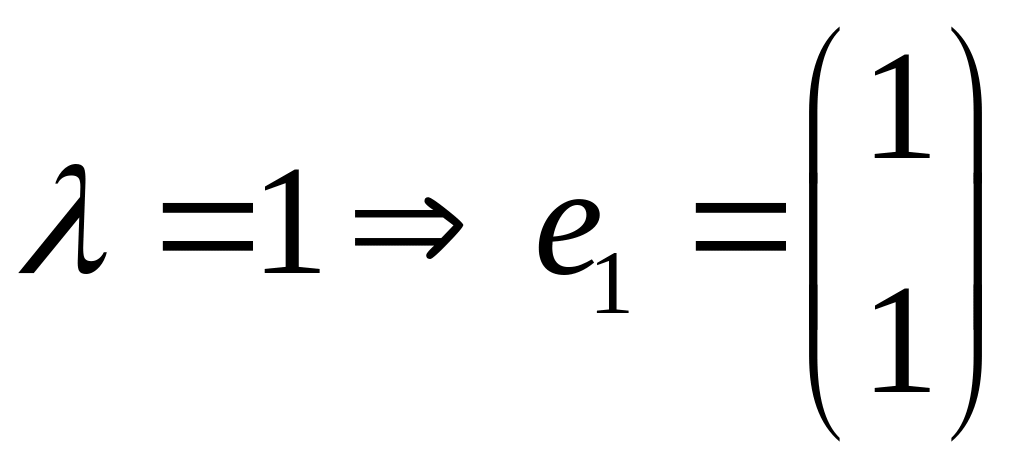
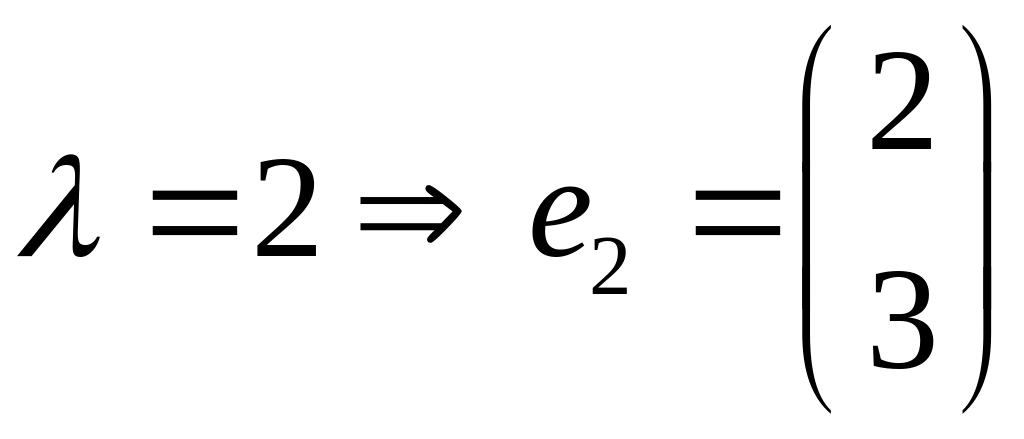
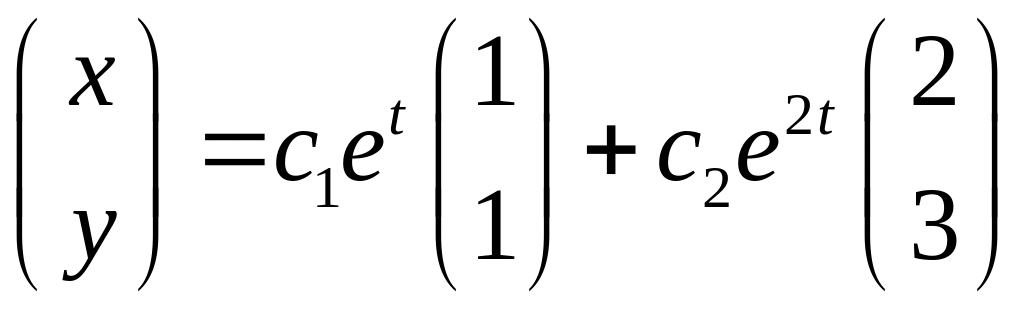
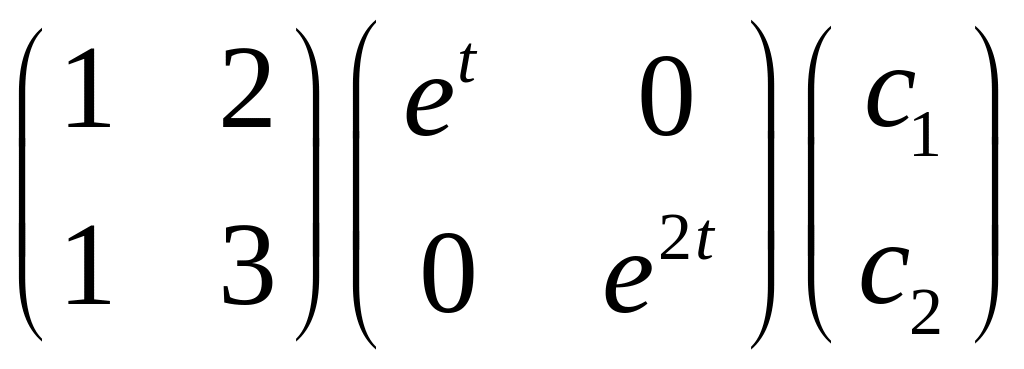
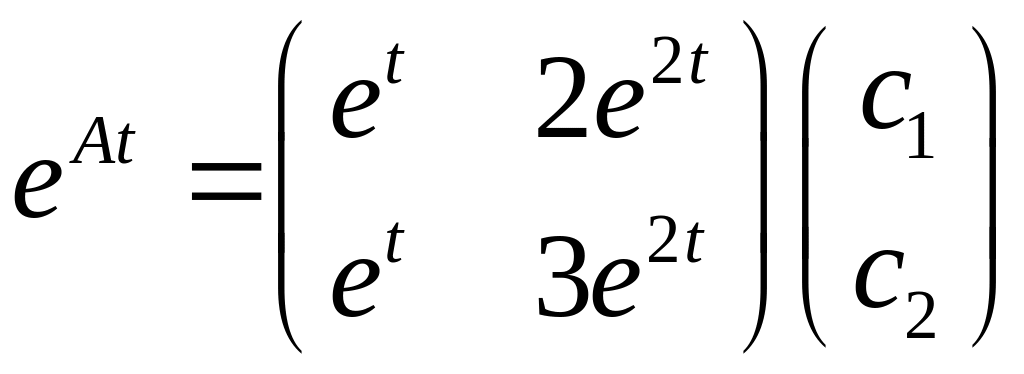
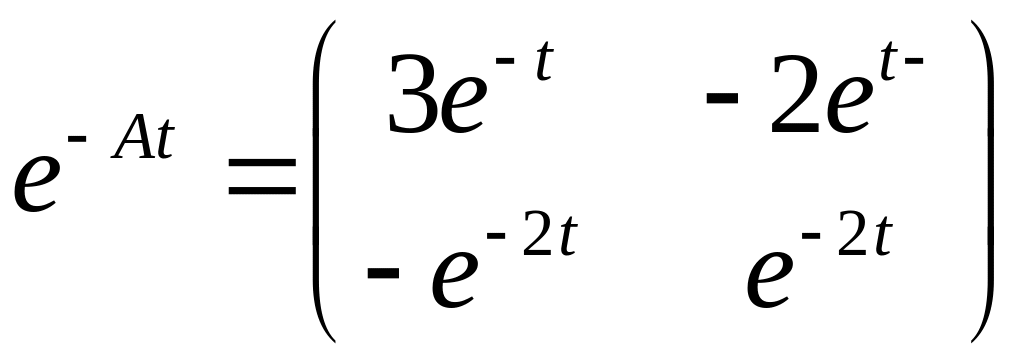
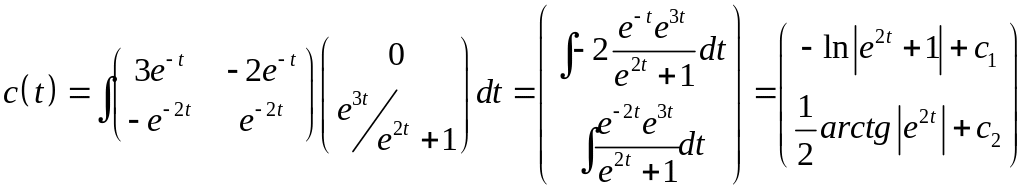
Теорема о существовании единственности (тсе)
Теорема (Для одного уравнения 1-го порядка)
Пусть функция
![]() и
и
![]() непрерывны в некоторой
области
непрерывны в некоторой
области
![]() ,
тогда для любой точки
,
тогда для любой точки
![]()
![]() задача Коши:
задача Коши:
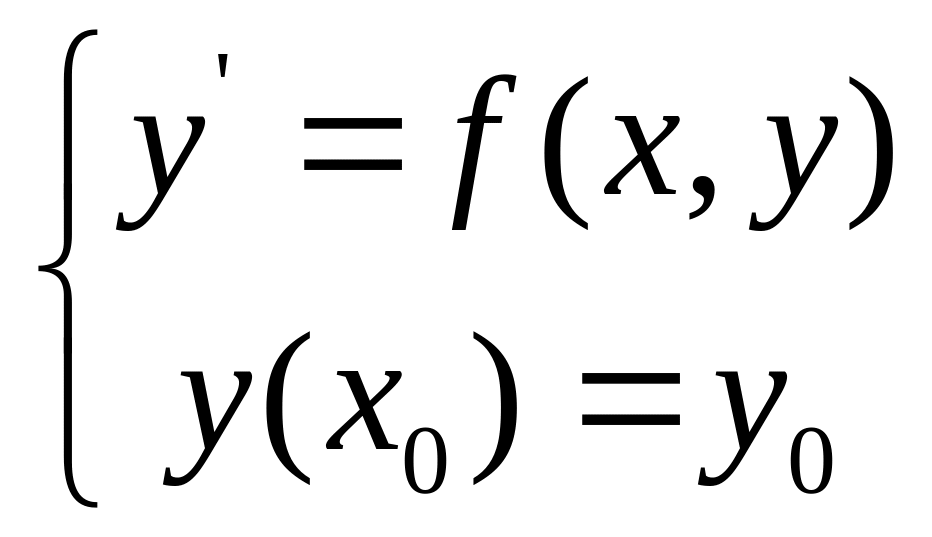
имеет единственное решение.
Замечание:
найденное решение находится локально
(решение задано на малом интервале,
содержащем точку
![]()
![]() ,
некоторое
,
некоторое
![]() .
.
Доказательство:
1) сведение задачи Коши к интегральному уравнению.
Теорема.
Задача Коши эквивалентна интегральному
уравнению:
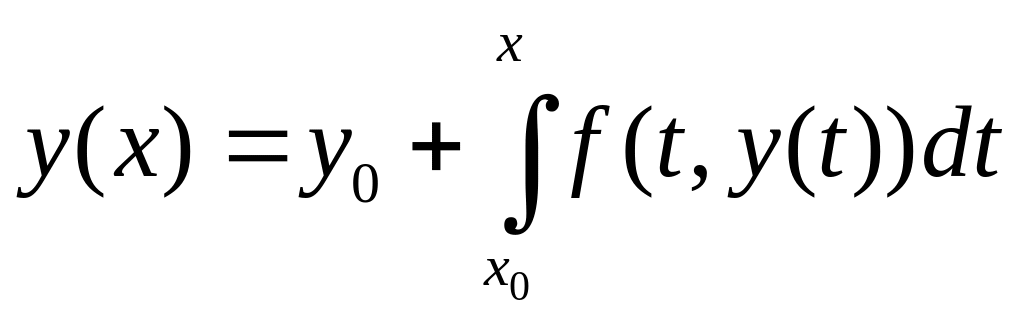 ,
,
y(x) – неизвестная функция.
Доказательство:
![]() :
проинтегрируем дифференциальное
уравнение.
:
проинтегрируем дифференциальное
уравнение.
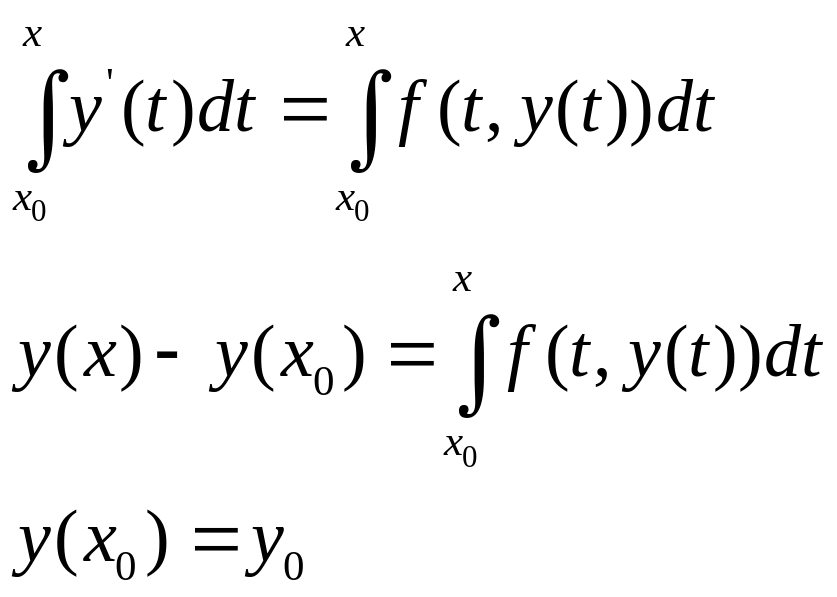
![]() :
дифференцируемое интегральное уравнение:
:
дифференцируемое интегральное уравнение:
![]() ,
получили дифференциальное уравнение.
,
получили дифференциальное уравнение.
Проверим начальные данные:
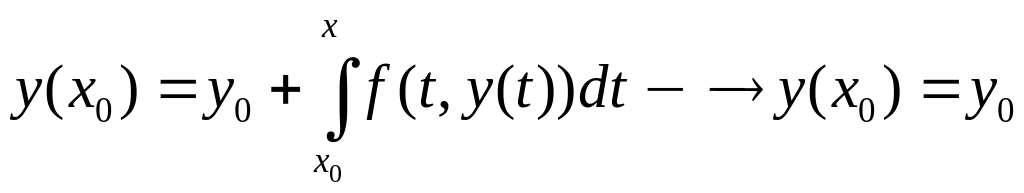
-начальные данные
2) Применение метода последовательных приближений.
Определим отображение Пикара:
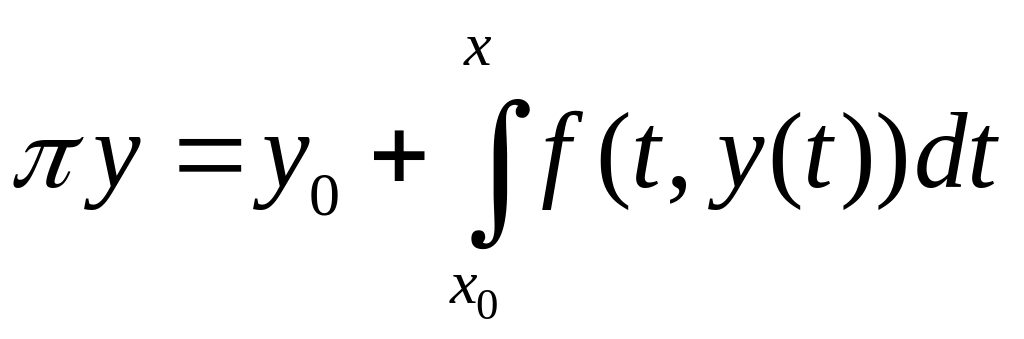
Рассмотрим итерации
отображений Пикара:
![]() - тождественный оператор (
- тождественный оператор (![]() )
)
![]() и т.д.
и т.д.
![]()
Можно взять первое
приближение:
![]() ,
рассмотрим
,
рассмотрим
![]() …
…
Оказывается, последовательность этих операторов сходится к задаче Коши и интегральному уравнению.
3. Теорема Банаха (о неподвижной точке)
X – метрическое пространство (в нем задана метрика - расстояние).
Определение:
Отображение
![]() называется
сжатым, если
называется
сжатым, если
![]()
![]() ,
что для любых точек
,
что для любых точек
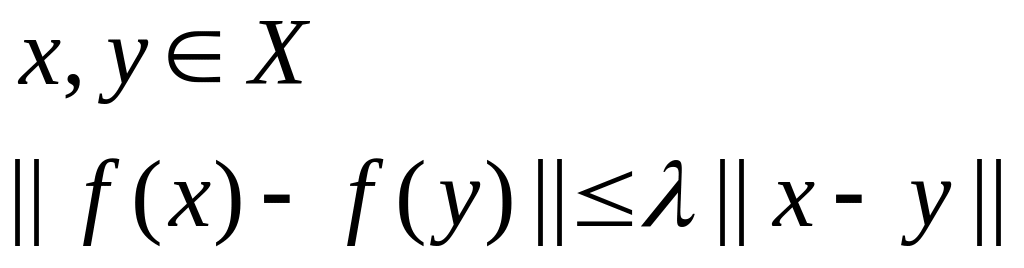
Теорема Банаха.
Сжатое отображение
полного метрического пространства
имеет единственную неподвижную точку
(т.е. существует единственное
такое, что
![]() ).
).
Доказательство.
В полном отображении
нет пустот. Возьмем любую точку
![]() .
Рассмотрим последовательные образы
нашей точки:
.
Рассмотрим последовательные образы
нашей точки:
![]()
Оказывается, что
![]() сходится
как раз к неподвижной точке.
сходится
как раз к неподвижной точке.
Оценим расстояние при больших номерах n и m:
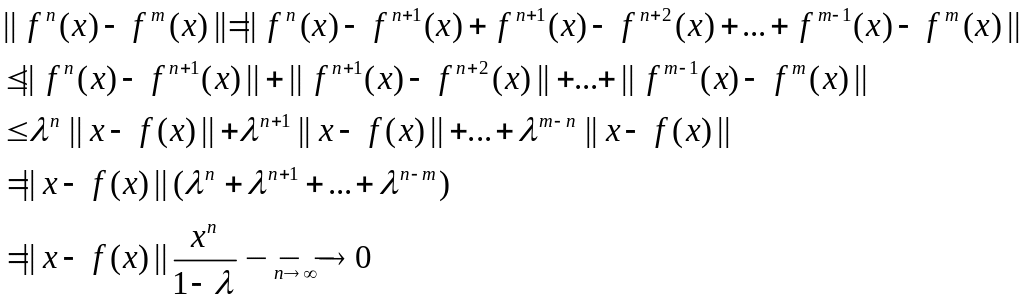
Вывод: следовательно, последовательность фундаментальна, следовательно, в полном пространстве сходится
![]()
Проверим, что - неподвижная точка
![]()
Единственность:
пусть
![]() две неподвижные точки
две неподвижные точки
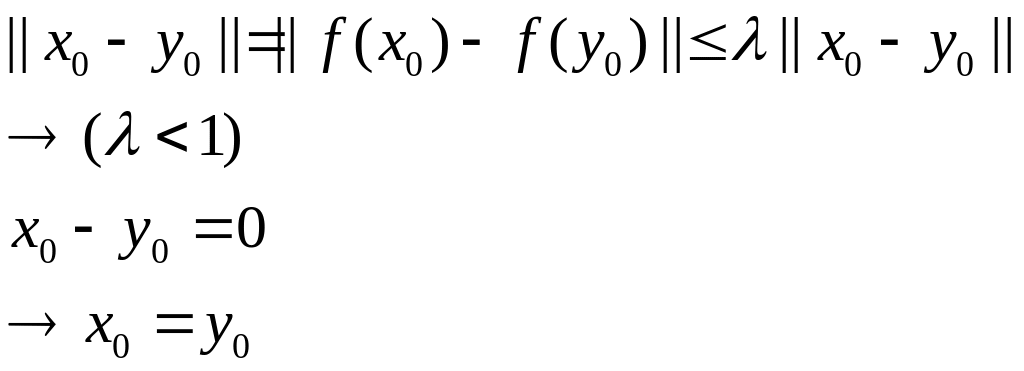
4. Применение теоремы Банаха отображением Пикара.
Определим 2 const.
![]()
Возьмем
столь малое:
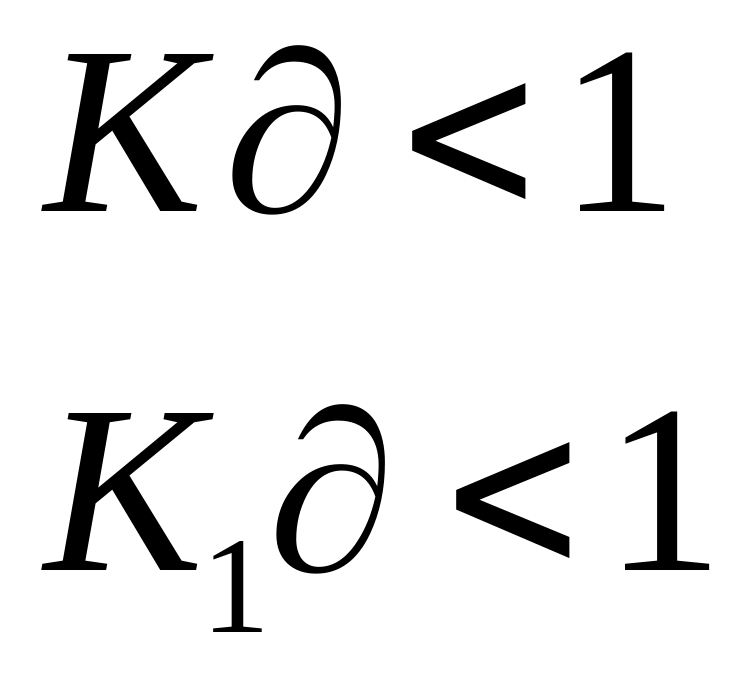 обозначим большее число:
обозначим большее число:![]()
Определим метрическое
пространство функций, заданных на
отрезке
таких, что
![]() ,
обозначим это пространство: X
(это метрическое пространство).
,
обозначим это пространство: X
(это метрическое пространство).
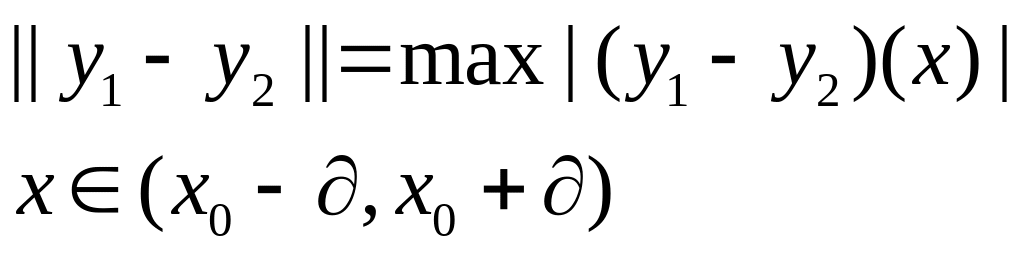
Для применения теоремы Банаха, надо проверить, что:
отображение Пикара действует из x в X
что
![]() сжатое
сжатое
![]() - непрерывная функция заданная на
- непрерывная функция заданная на
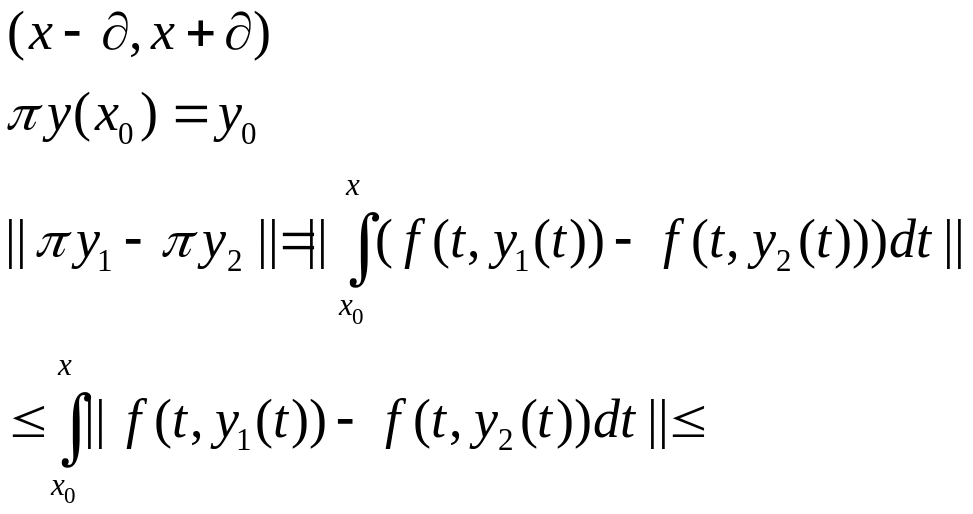
по теореме о конечных приращениях:
![]()
Надо проверить:
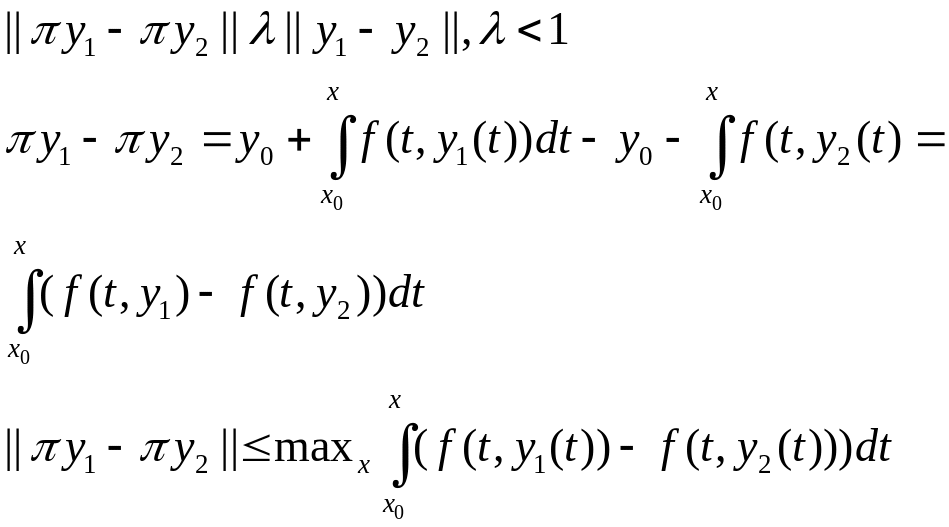
Теорема о конечных приращениях.
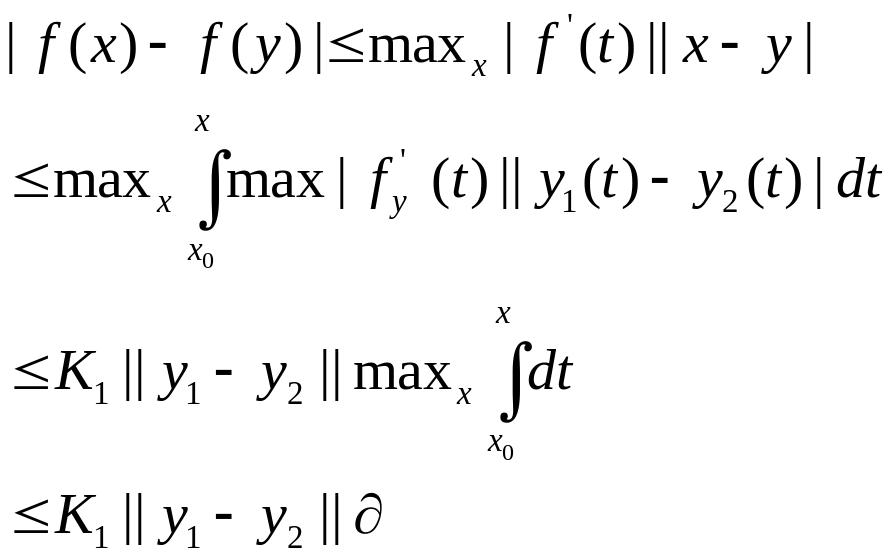
Возьмем таким малым, чтобы
![]()
Значит, имеем: метрическое пространство, в нем действует отображение Пикара, следовательно, имеем единственную неподвижную точку.
![]()
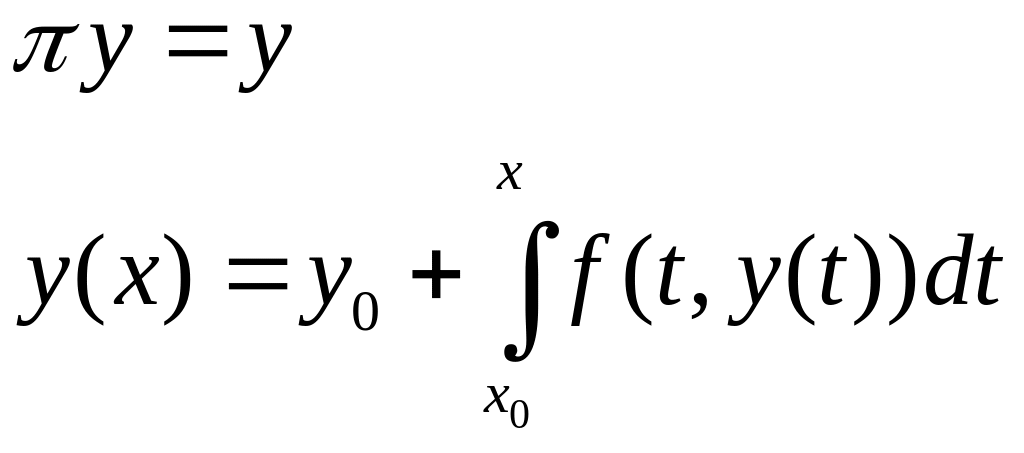
y – решение интегрального уравнения, следовательно решили задачу Коши.
Предложение решений.
Решение задачи Коши.
Задана в области
![]() может быть продолжена до границы области
G.
может быть продолжена до границы области
G.
Пример.
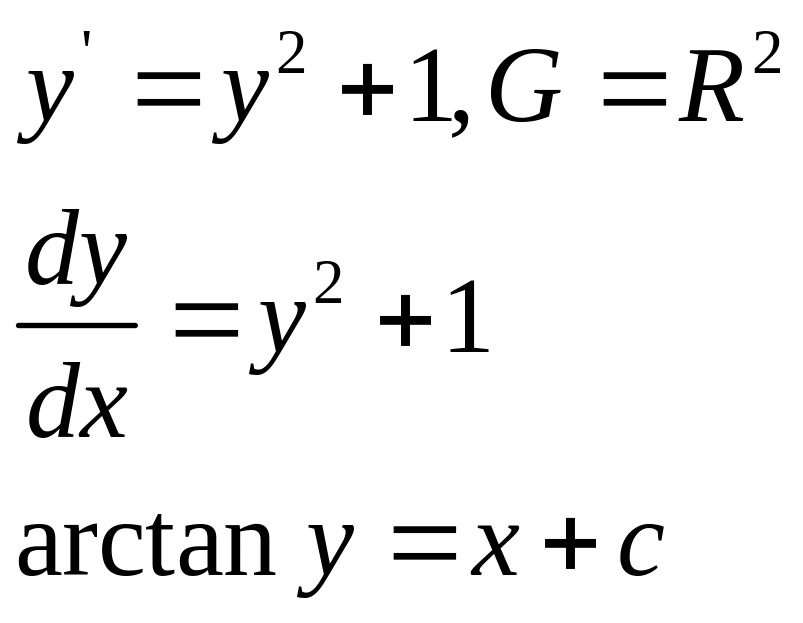
график
Проверка:
![]() начальные
данные
начальные
данные
![]() - решение заданное
на интервале (
- решение заданное
на интервале (![]() )
)
Возьмем точку на
кривой (решении)
![]() и
еще раз решим задачу Коши.
и
еще раз решим задачу Коши.
На общей области
определения оба решения совпадают, т.о.
решение может продолжаться до границы
области. Продолжая мы дойдем до точки
![]() ,
если точка не лежит на границе а внутри,
можно снова применить задачу Коши,
следовательно наше предположение не
верно.
,
если точка не лежит на границе а внутри,
можно снова применить задачу Коши,
следовательно наше предположение не
верно.
Непрерывная и дифференцируемая от начальных данных и от параметров
Цель:
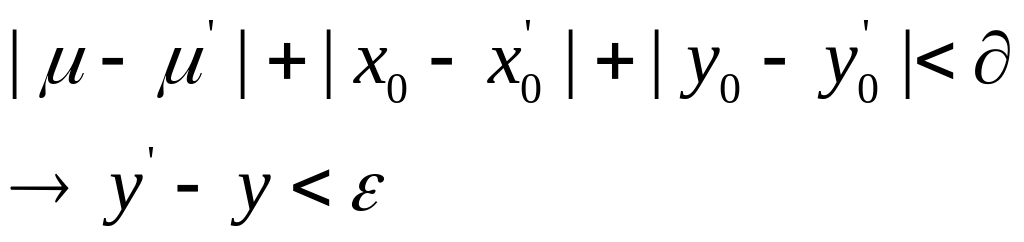
На некотором промежутке изменений переменных.
Надо повторить всю процедуру с отображением Пикара.
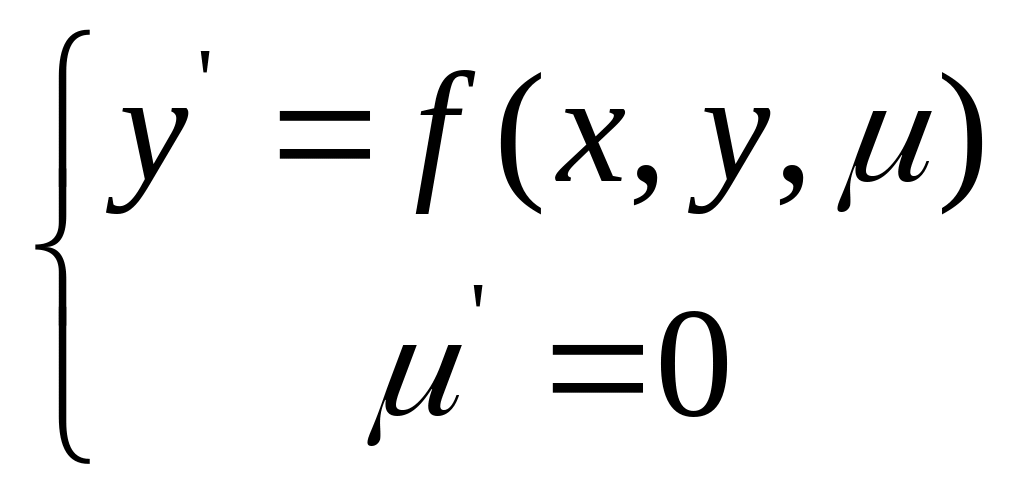
Линейные системы.
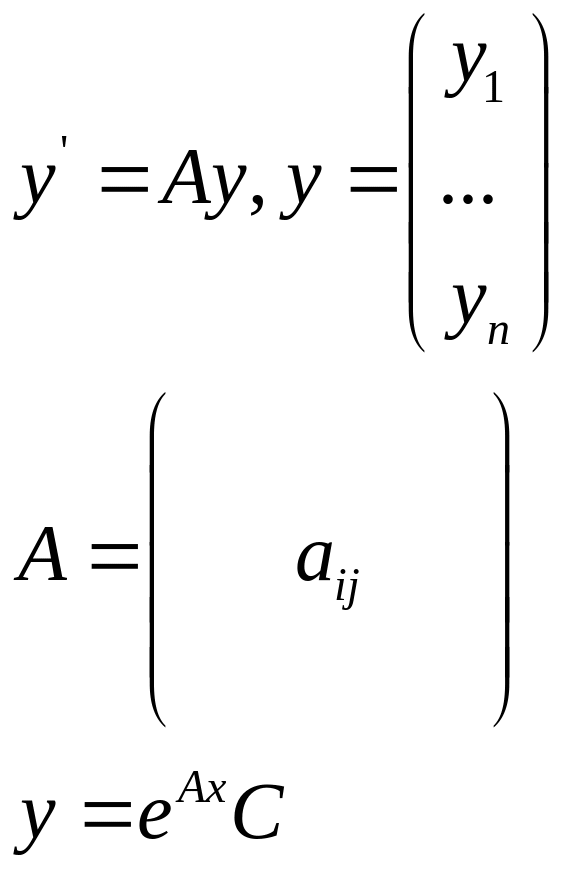
Теперь А=А(х) переменная матрица.
Теорема.
Множество решений линейной системы является линейным пространством размерности n.
Доказательство.
Х – множество
решений
![]() ,линейное
пространство
,линейное
пространство
Рассмотрим линейный оператор
![]()
В – изоморфизм, т.е.:
сюрьективно
нулевое ядро
![]()
В виду того, что существует решение задачи Коши
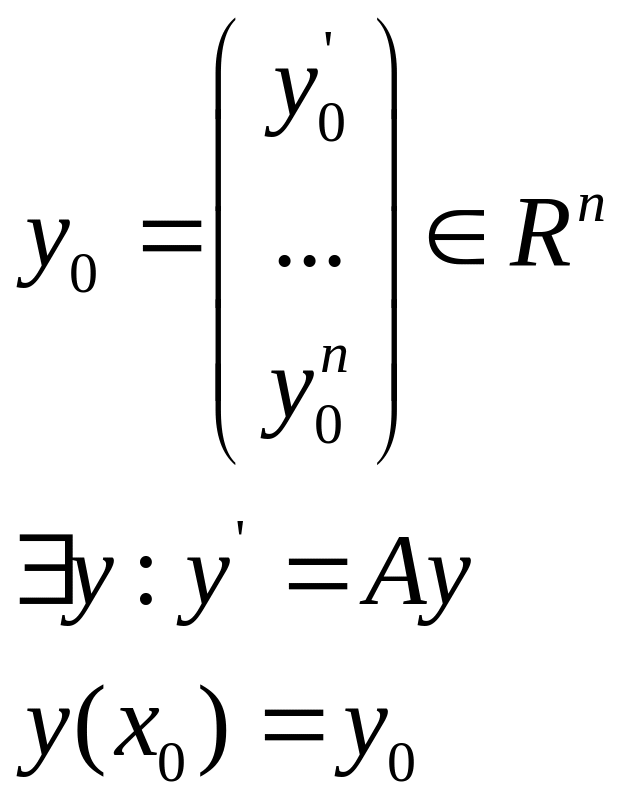
Для каких
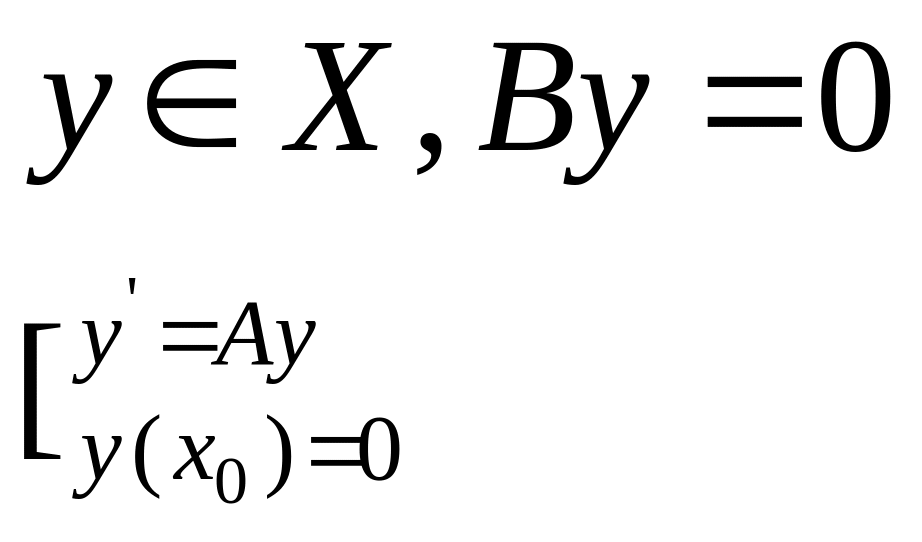
По теореме о
единственности
![]()
Базис пространства решений состоит из n-векторов функций. Этот базис называется фундаментальной системой решений.
 - общее решение.
- общее решение.
![]() - фундаментальная
матрица решений (матрициант).
- фундаментальная
матрица решений (матрициант).
Матрициант тоже
удовлетворяет:
![]()
![]() -
невырождена.
-
невырождена.
Определитель этой матрицы носит название матрицы Вронского.
Формула Луивилля.
![]() - система
дифференциальных уравнений 1-го порядка.
- система
дифференциальных уравнений 1-го порядка.
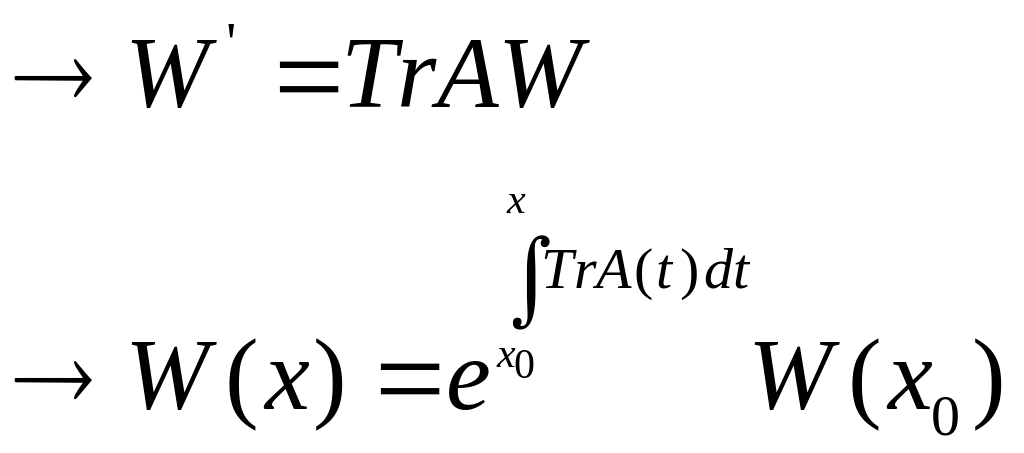
Доказательство:
1)A=const матрицы
Матрициант
![]()
![]()
Приведем матрициант к жордановой форме:
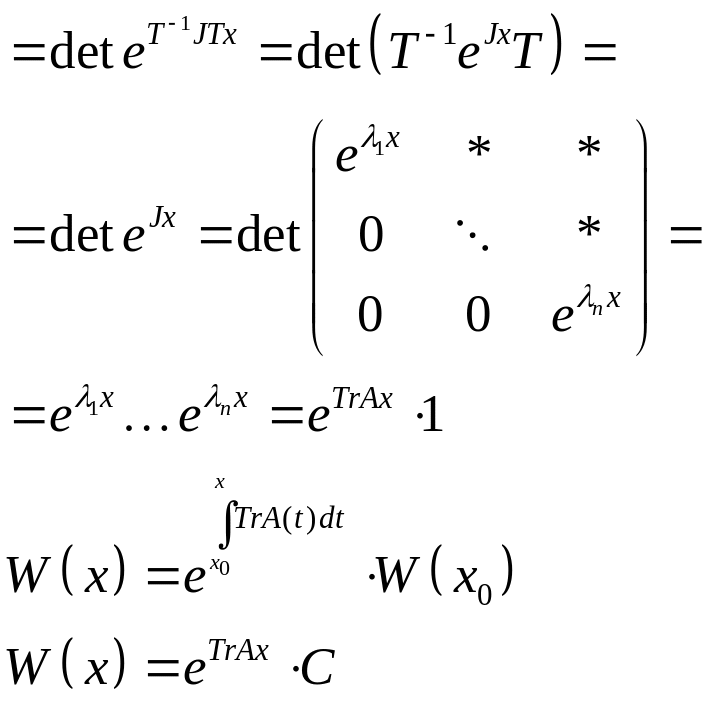
Доказательство:
формула Лиувилля в общем случае
Пусть
![]() –
фундаментальная матрица
–
фундаментальная матрица
![]()
Рассмотрим приращение фундаментальной матрицы:
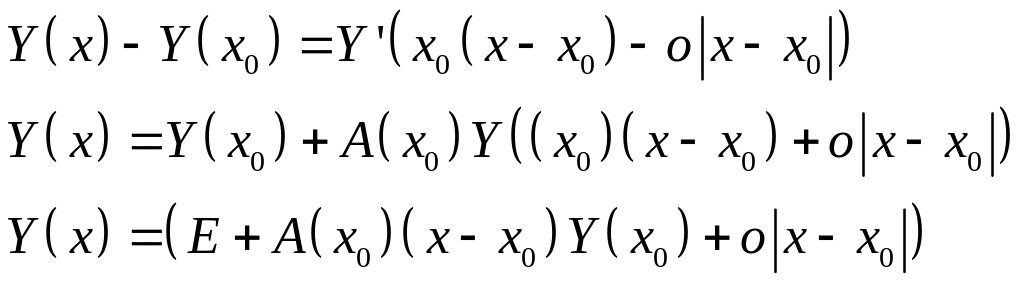
Возьмем определители от обоих частей матрицы:
![]()
Будем считать
![]() с точностью до
с точностью до
![]()
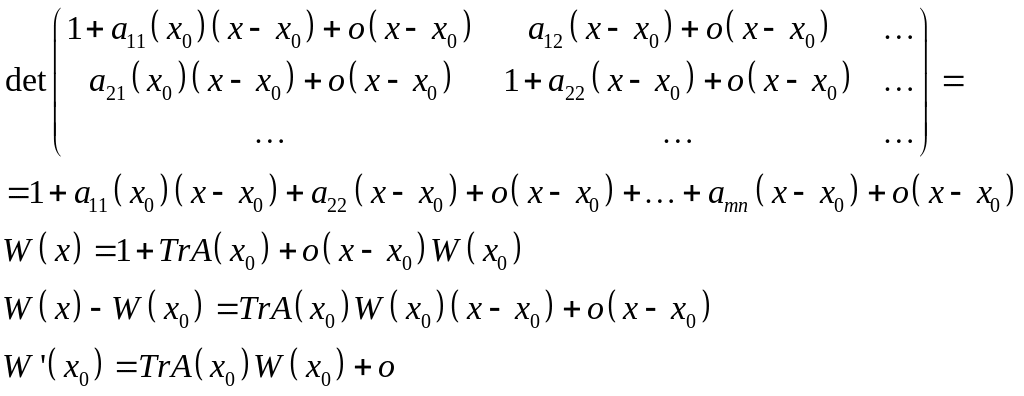
Решение неоднородных систем.
![]() (1)
(1)
Решение:
Решается неоднородная система:
- фундаментальная матрица
![]() ,
где С
вектор константа
,
где С
вектор константа
Решение неоднородной системы будем искать в таком же виде, но
![]() постоянная функция,
а не постоянный вектор
постоянная функция,
а не постоянный вектор
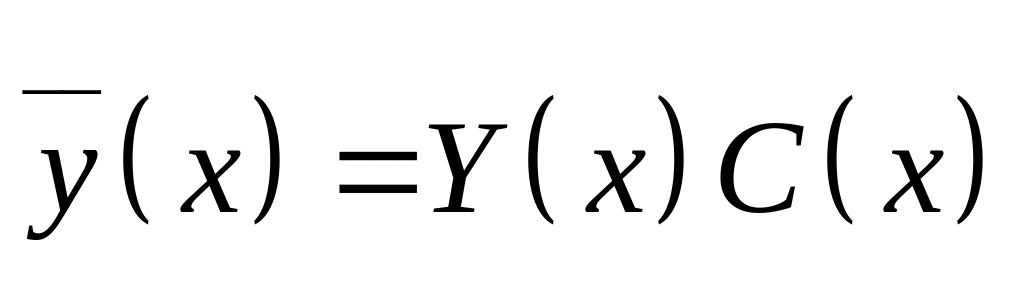
Подставим в систему (1):
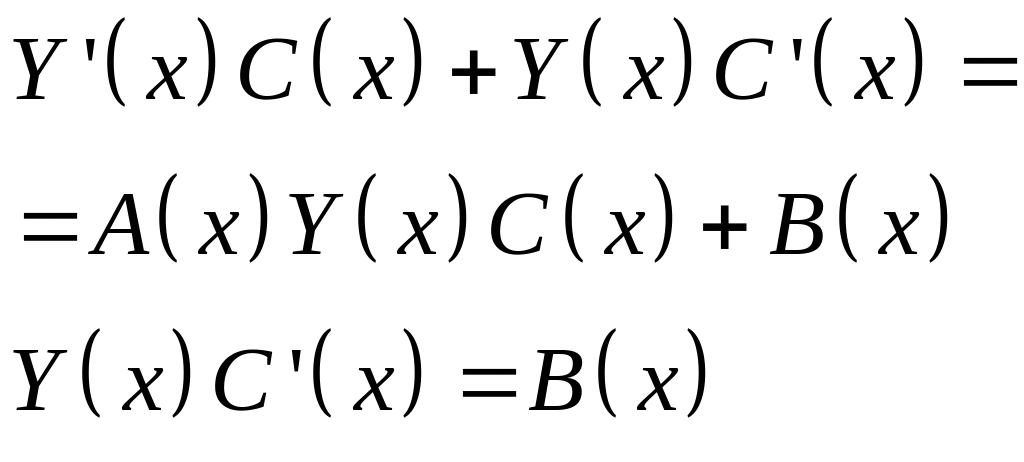 ,
,
где невырожденная матрица
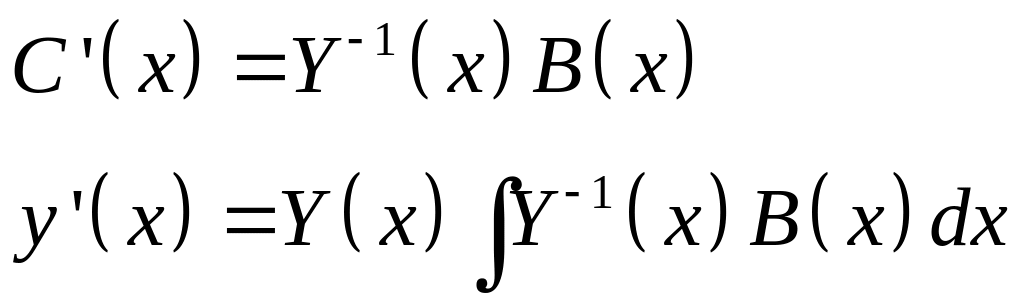
или в другом виде:
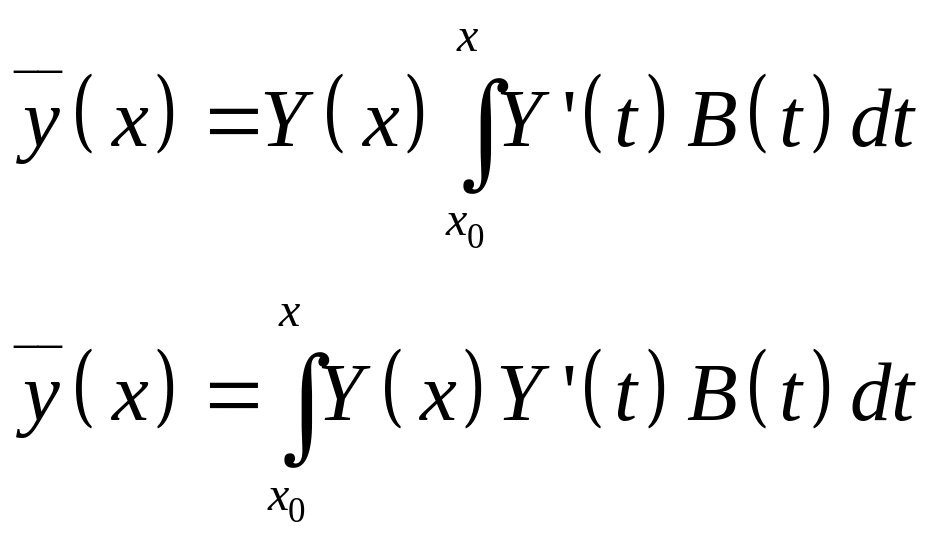
Случай уравнения n-ого порядка
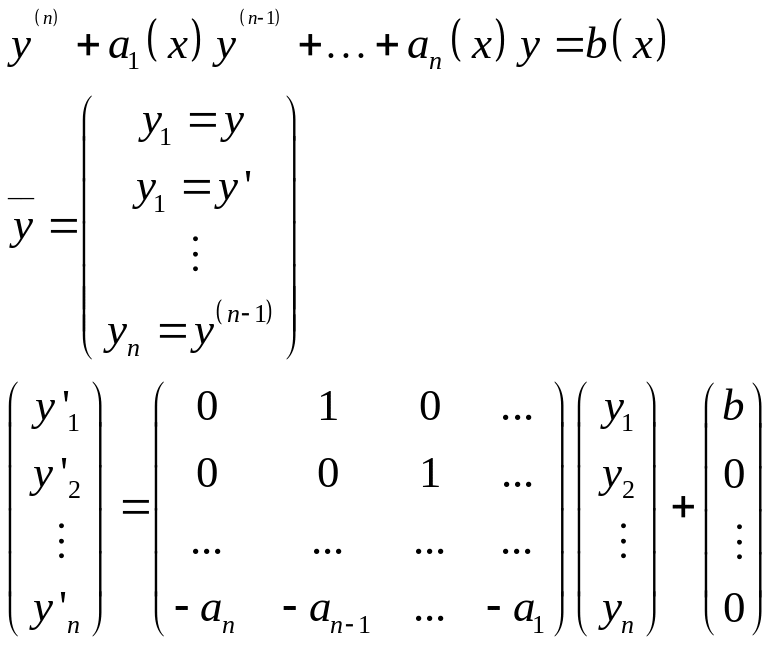
Если
![]() - ФСР для уравнения то:
- ФСР для уравнения то:
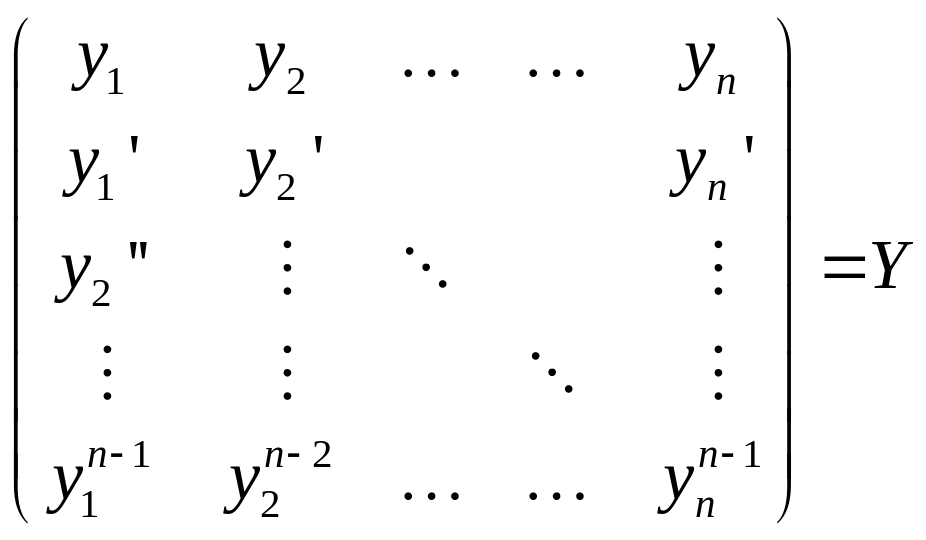
-фундаментальная матрица.
![]() - определитель
Вронского
- определитель
Вронского
![]()
Формула Лиувилля:
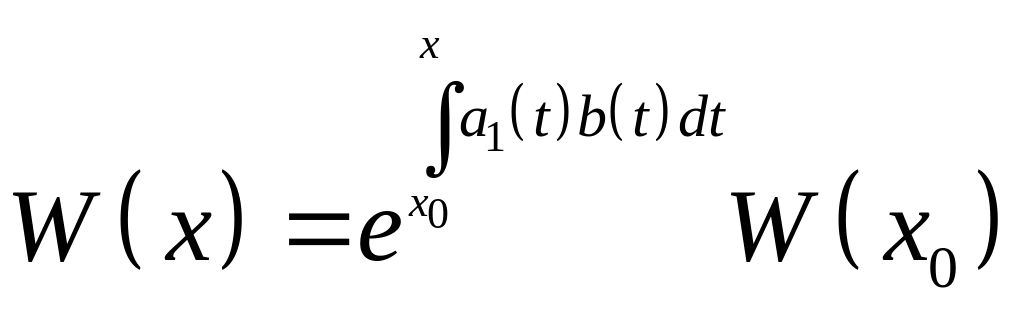
Неоднородные уравнения:
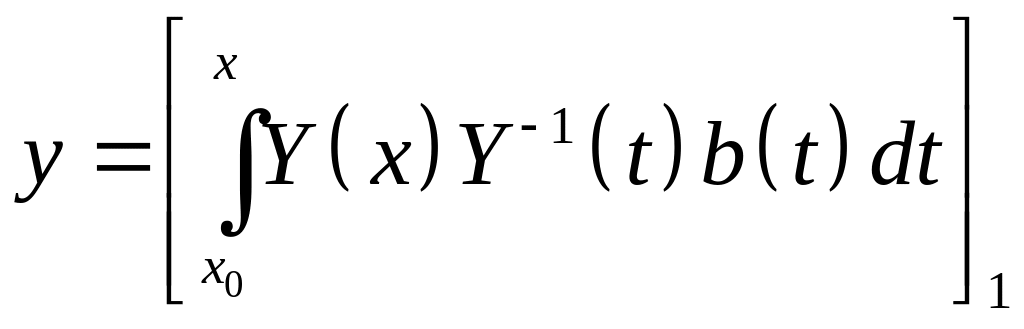
(надо взять только первую строку матрицы)
Элементы условия устойчивости.
Автономные системы дифференциальных уравнений:
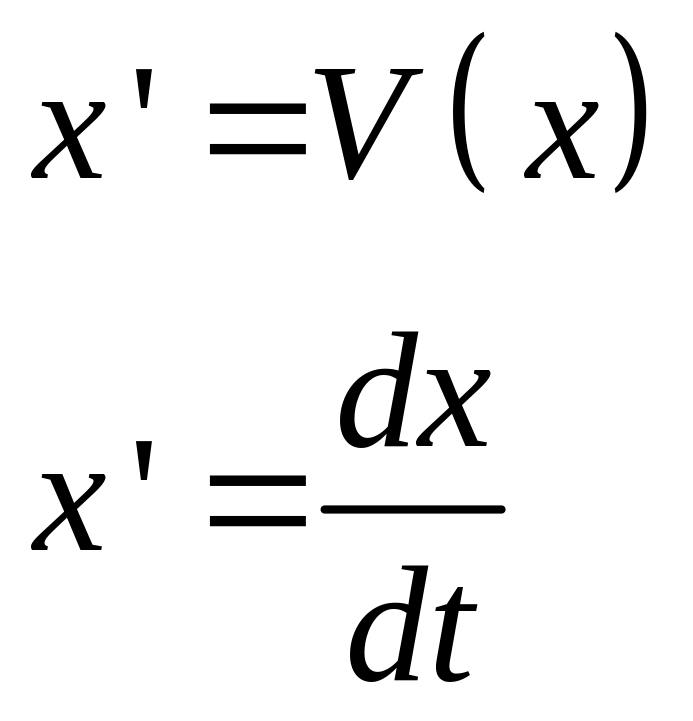 ,
где
,
где
![]() - вектор,
- вектор,
![]() - вектор функции.
- вектор функции.
Неавтономные системы дифференциальных уравнений:
![]()
Повышая размерность неавтоматизированную систему можно привести к автономному виду.
Вводим новый вектор:
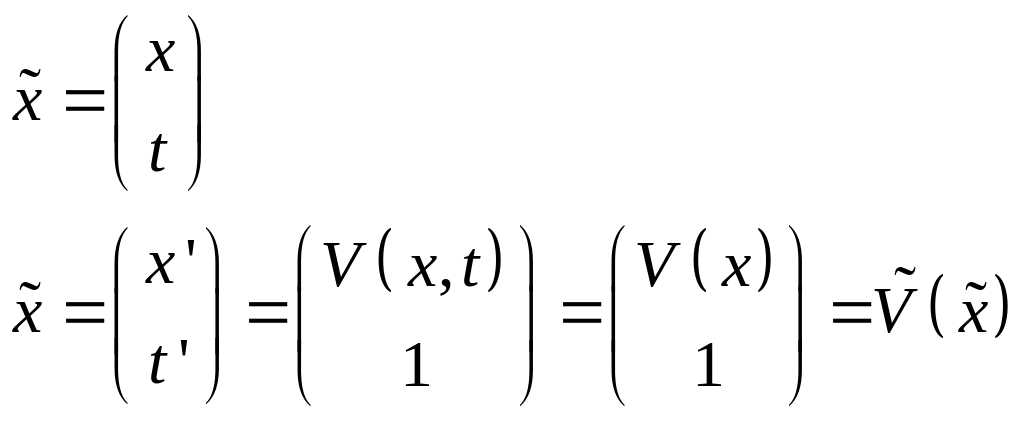
Вектор – функция называется векторным полем.
График
График решения называется интегральной кривой.
Образ графика в
![]() называется фазовой кривой
называется фазовой кривой
График(интегральная кривая и фазовая кривая)
Решить задачу Коши, это значит найти такую фазовую кривую, проходящую через заданную точку.
Фазовая кривая имеет касательный вектор, совпадающий с векторным полем в данной точке
Утверждение: Различные фазовые кривые не пересекаются это следует из ТСЕ
Виды фазовых кривых:
точка
гладкая кривая без самопересечения
замкнутая фазовая кривая – цикл
График
Определение: точки,
в которых
![]() - точки самопересечения (или покоя)
- точки самопересечения (или покоя)
Если
,
то фазовая кривая
![]() представляет собой точку
представляет собой точку
![]()
Любая фазовая кривая гладкая
![]() - фазовая кривая,
- фазовая кривая,
![]()
В данной системе два касательных вектора совпадают:
График График
В этом месте нарушается ТСЕ.
Вывод: гладкая кривая не может пересекаться.
Теорема о выпрямлении векторного поля.
График
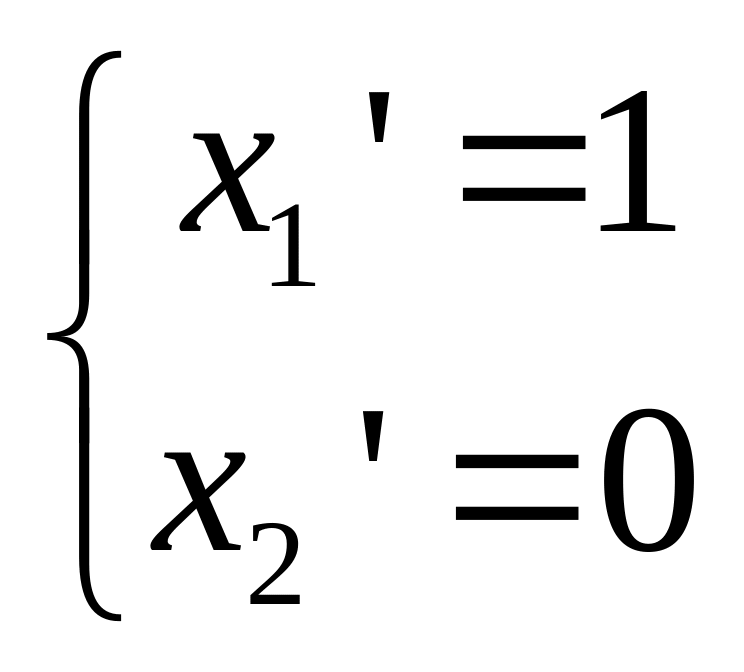
Рассмотрим две основные точки:
График
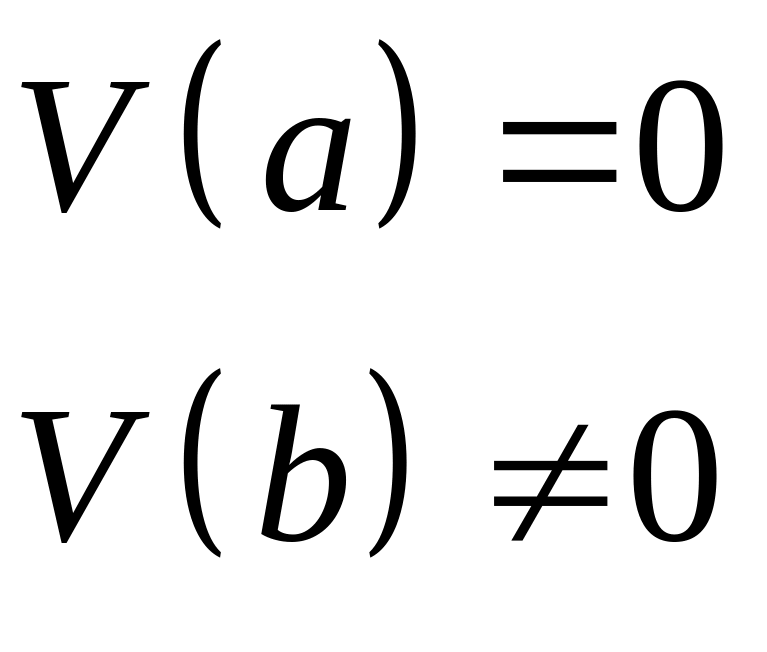
- непрерывна
Вывод: зная положение равновесия можно восстановить поведение фазовых кривых, так как окрестности не особых точек поле параллелезуемо.
Пусть
![]() не является положением равновесия
не является положением равновесия
![]() ,
тогда существует невырожденная замена
координат
,
тогда существует невырожденная замена
координат
![]() ,
что в новых координатах, векторное поле
постоянно и система выглядит так:
,
что в новых координатах, векторное поле
постоянно и система выглядит так:
График
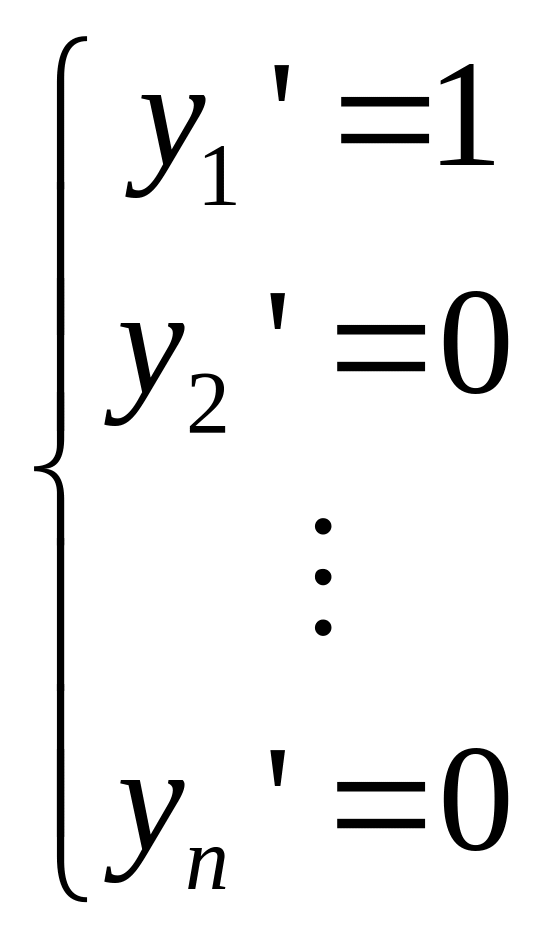
Замена координат.
Локально:
График График
График
Пусть точка
![]() близкая к
близкая к
![]() может лежит на фазовой кривой с декартовыми
координатами
может лежит на фазовой кривой с декартовыми
координатами
![]() .
Возьмем первую координату точку
пересечения фазовой кривой и прямой
.
Возьмем первую координату точку
пересечения фазовой кривой и прямой
![]() ,
обозначим ее
.
Фазовая кривая:
,
обозначим ее
.
Фазовая кривая:
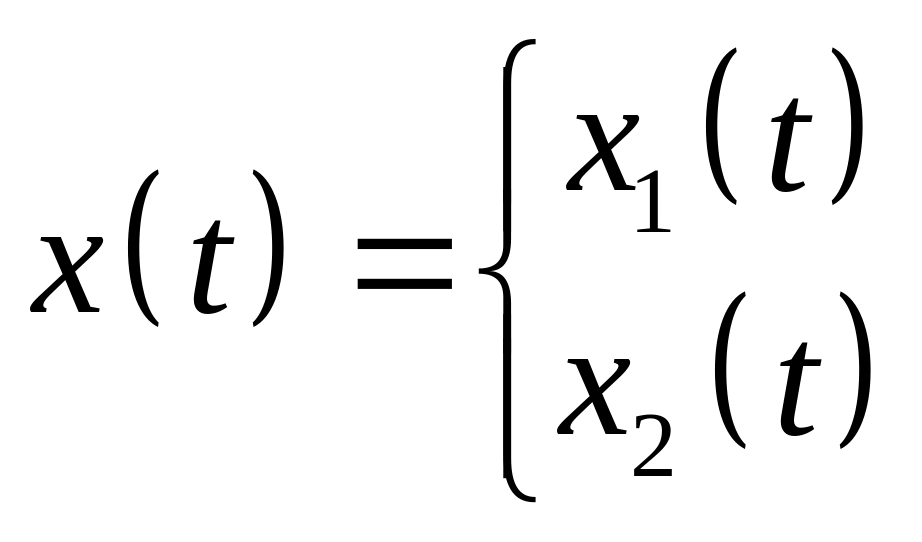 ,
,
Проходящая через
точку
![]() в момент
в момент
![]()
Вторая координата
![]()
В новых координатах векторное поле постоянно
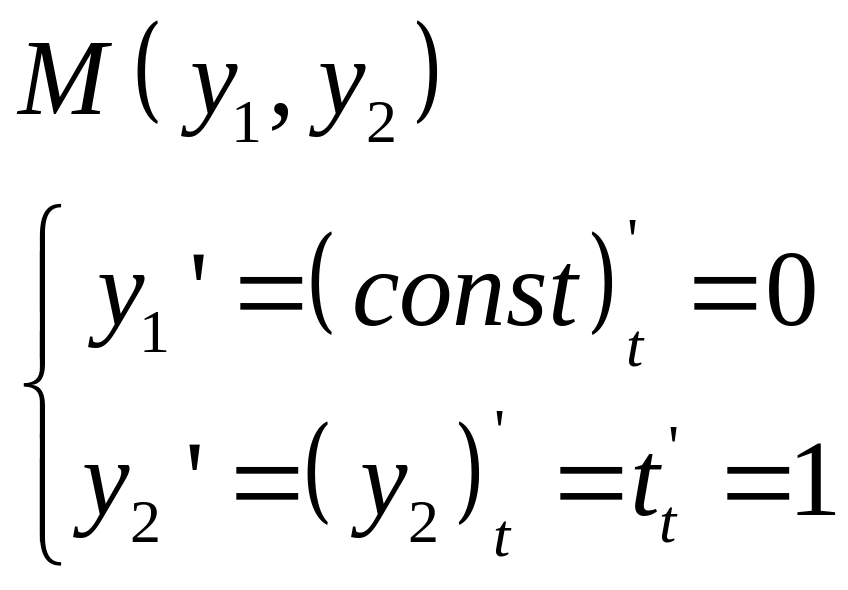
Для того чтобы проверить не…….!!!!! Надо подсчитать якобиант перехода одних координат в другие.
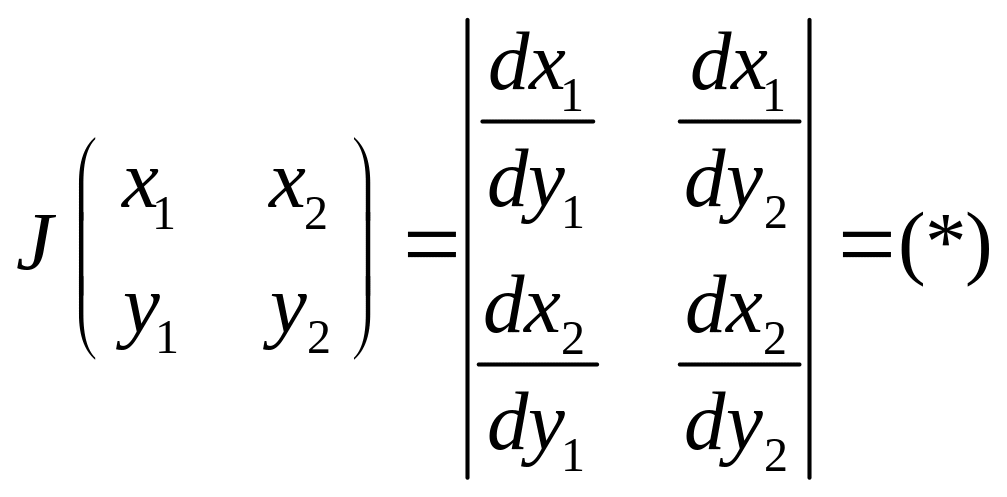
Достаточно найти
![]() в
точке
в
точке
![]() ,
,
В ближайших точках.
В точке
координаты
![]() совпадают
совпадают
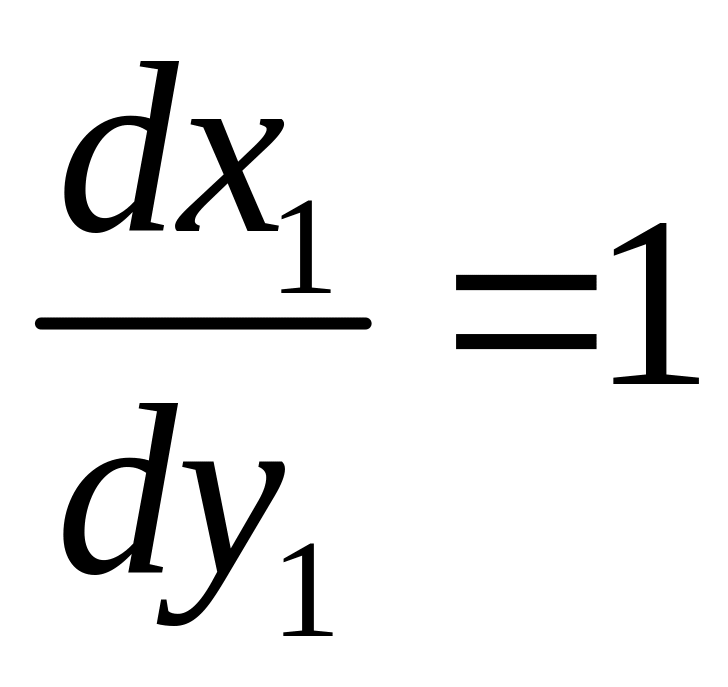
В точке
координаты
![]() равны.
равны.
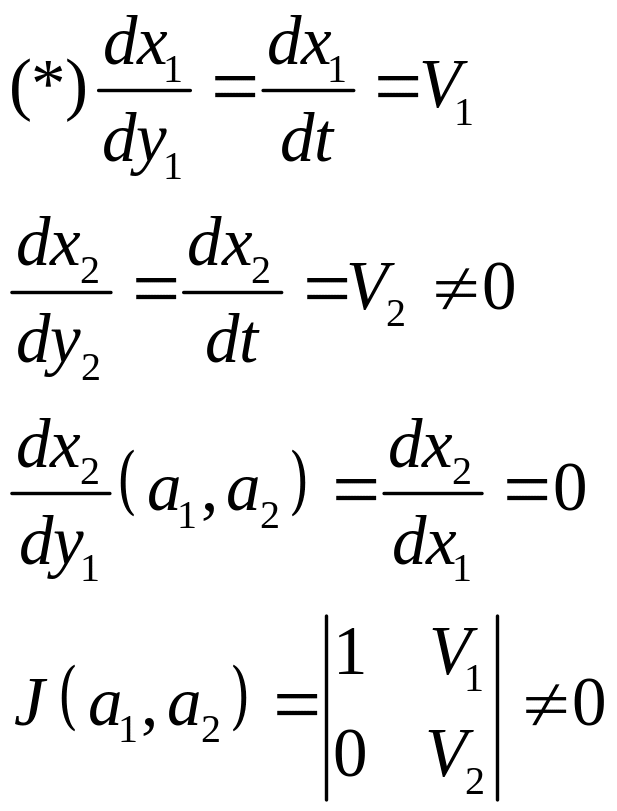
Исследование положения равновесия.
Определение:
Положение равновесия
![]() является устойчивым (по Ляпунову), если
для
является устойчивым (по Ляпунову), если
для![]() ,
то для фазовой кривой, проходящей через
точку
,
,
то для фазовой кривой, проходящей через
точку
,
![]() для
для
![]()
График
Определение: Положение равновесия является асимптотически устойчивой если:
устойчиво по Ляпунову
![]()
График
Функция Ляпунова.
Квадратичная форма
![]()
-квадратичная форма
![]() -положительно
определенная
-положительно
определенная
Если ![]()
![]() положительно полу определена на
положительно полу определена на ![]() ,
если
,
если ![]()
Производная Ли
(производная в силу векторного поля)
Пусть ![]() в
в ![]()
– векторное поле в
![]() – система
дифференциальных уравнений
– система
дифференциальных уравнений
![]() - фазовая
кривая
- фазовая
кривая
Рассмотрим сложную
функцию ![]()
График
Обычная производная
функции ![]() называется производной Ли
в силу векторного поля
называется производной Ли
в силу векторного поля
![]()
Раньше :
![]()
![]() не убывает вдоль фазовых кривых
не убывает вдоль фазовых кривых
Квадратичная форма
называется функцией Ляпунова для
векторного поля
в окрестности ![]() если:
если:
1)
![]() положительно определенная
положительно определенная
2)![]() отрицательно полуопределенная
отрицательно полуопределенная
Теорема (Ляпунова об устойчивости).
Пусть - векторное поле, - положение равновесия, - устойчиво, если в окрестности точки найдется функция Ляпунова.
Доказательство:
Считаем, что
![]()
![]() ,
то фазовая кривая, проходящая через
точку
,
не выйдет за круг радиуса
,
то фазовая кривая, проходящая через
точку
,
не выйдет за круг радиуса
![]() .
.
![]()
Пусть найдена функция Ляпунова.
![]()
Фиксируем:
![]()
Подберем такое
![]() ,
чтобы
,
чтобы
![]() было меньше чем
было меньше чем
![]() (
(![]() ,
при
,
при
![]() ).
Пусть
).
Пусть
![]() .
Рассмотрим фазовую кривую, проходящую
через точку
.
У функции
производная Ли:
,
значит
не возрастает вдоль фазовых кривых,
.
Рассмотрим фазовую кривую, проходящую
через точку
.
У функции
производная Ли:
,
значит
не возрастает вдоль фазовых кривых,
![]() ,
где
,
где
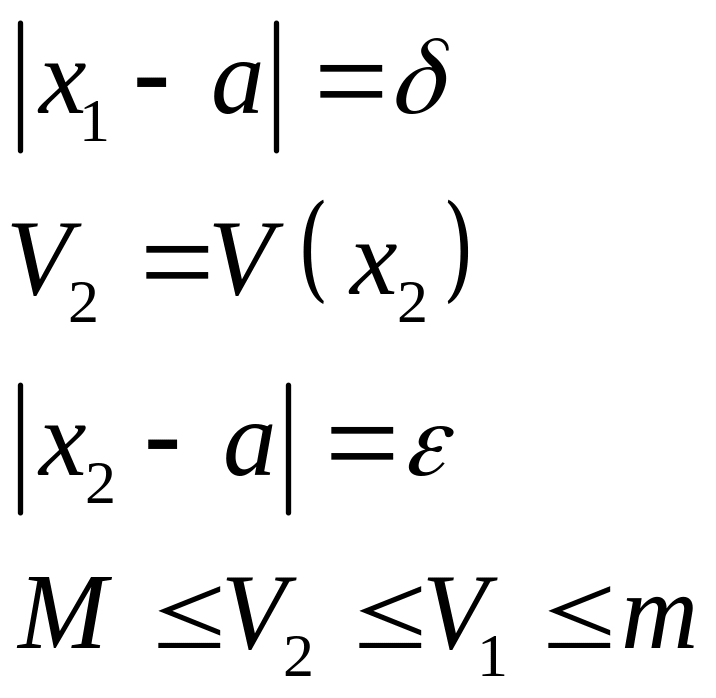
![]() ,
что противоречит выбору
,
что противоречит выбору
![]() .
Фазовая кривая не может выйти за пределы
круга.
.
Фазовая кривая не может выйти за пределы
круга.
Теорема (Ляпунова об асимптотической устойчивости)
Положение равновесия асимптотически устойчиво, если для функции Ляпунова выполняются строгие неравенства:
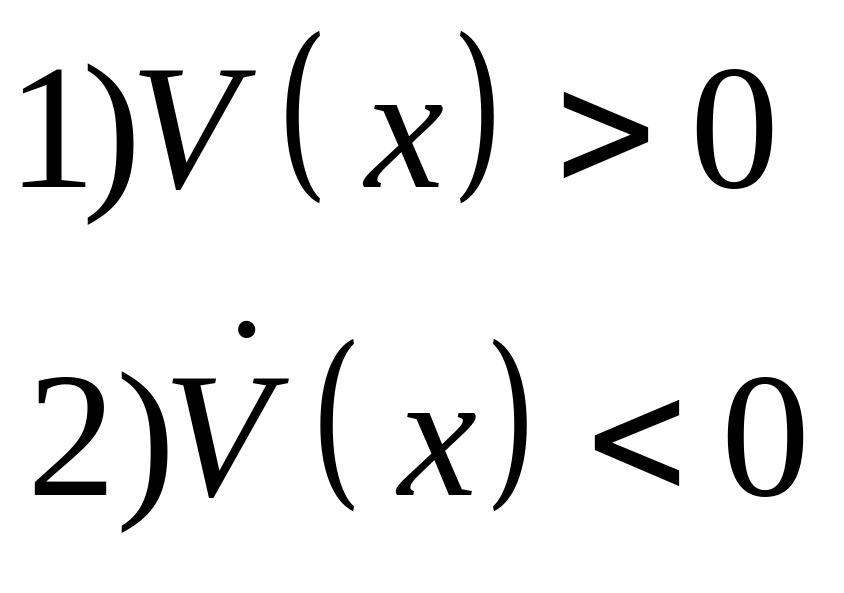
Доказательство:
(Надо
![]() )
)
убывает вдоль фазовых кривых
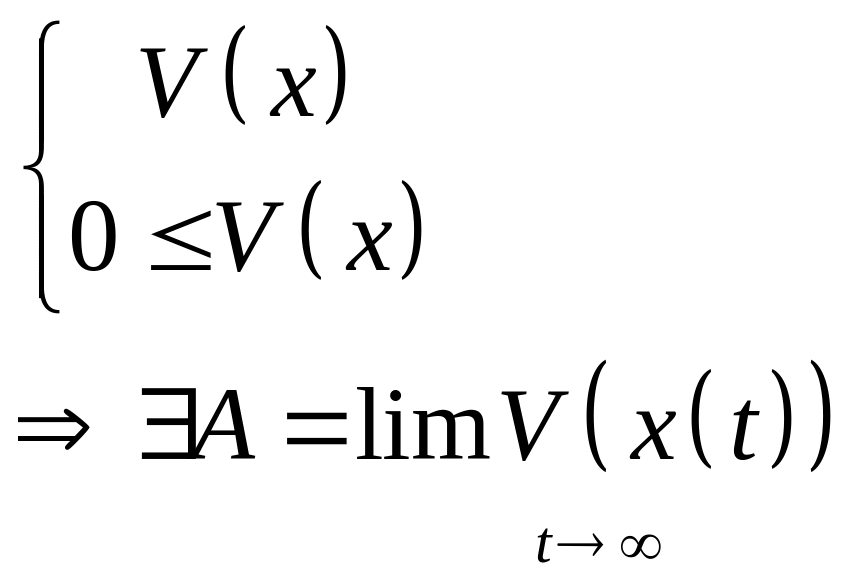
![]() ,
то есть
,
то есть
![]()
Доказано.
![]()
Покажем, что такого быть не может. Кроме того
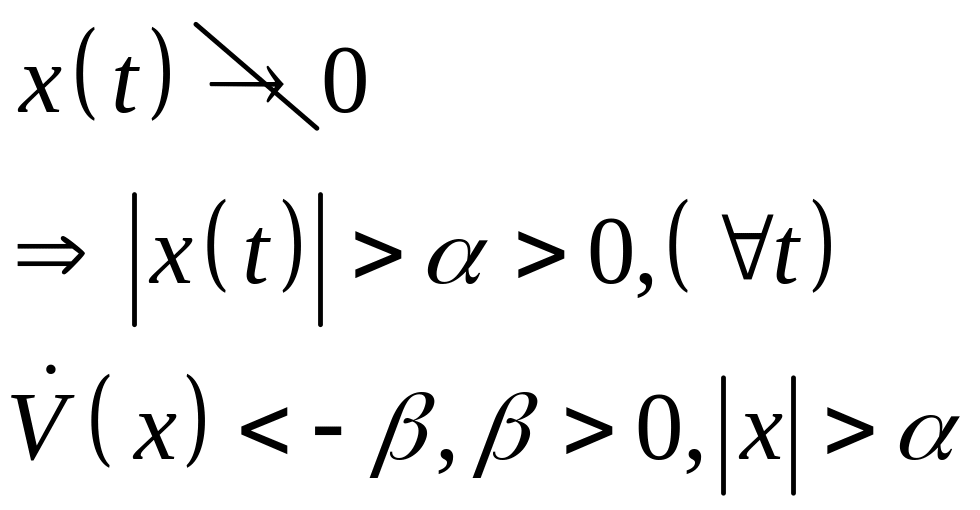
График
Проинтегрируем неравенство:
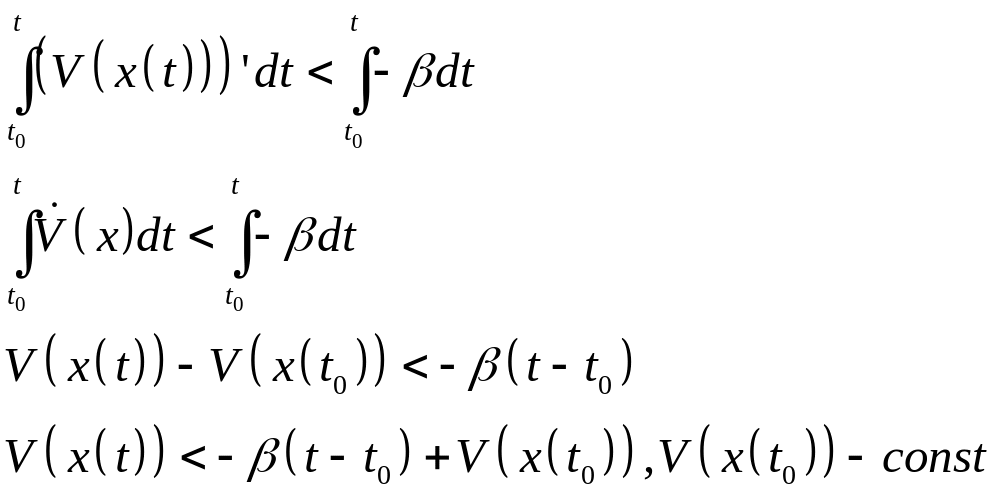
Причем при
![]() стремиться к
стремиться к![]() ,
что противоречит условию, что
,
что противоречит условию, что
![]() .
.
Устойчивость линейных систем.
![]()
Векторное поле:
![]()
![]()
Матрица A не
вырождена
![]() -единственное
положение равновесия.
-единственное
положение равновесия.
Теорема.
асимптотически
устойчиво
![]()
![]() (вещественное
значения собственных чисел больше
нуля),
устойчиво, если
(вещественное
значения собственных чисел больше
нуля),
устойчиво, если
![]() и нет кратных собственных значений. Во
всех остальных случаях положения
равновесия не устойчивый узел, фокус,
седло.
и нет кратных собственных значений. Во
всех остальных случаях положения
равновесия не устойчивый узел, фокус,
седло.
Доказательство№1:
(используем явный вид решения)
Общее решение системы имеет вид:
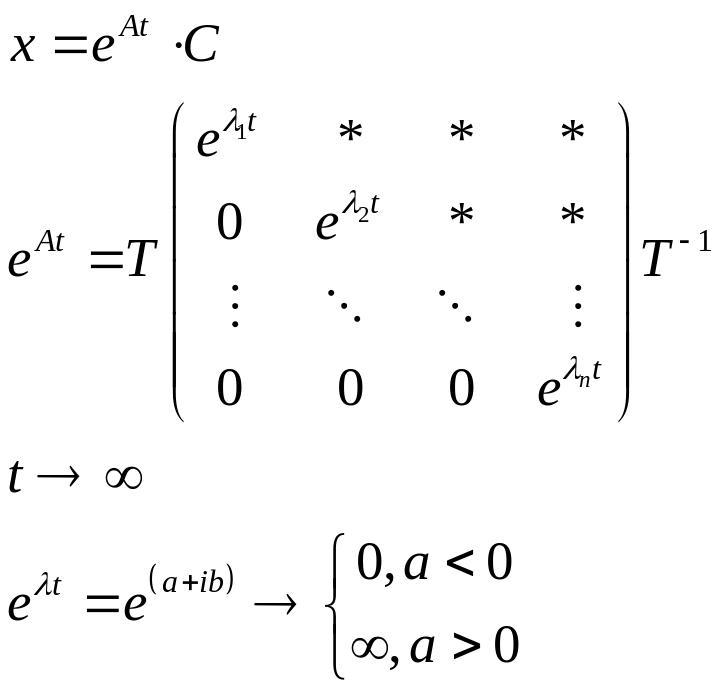
если все
,
![]() быстрее чем любой многочлен, следовательно
устойчиво асимптотически.
быстрее чем любой многочлен, следовательно
устойчиво асимптотически.
нет
кратных для тех
![]() ,
для которых
,
для которых
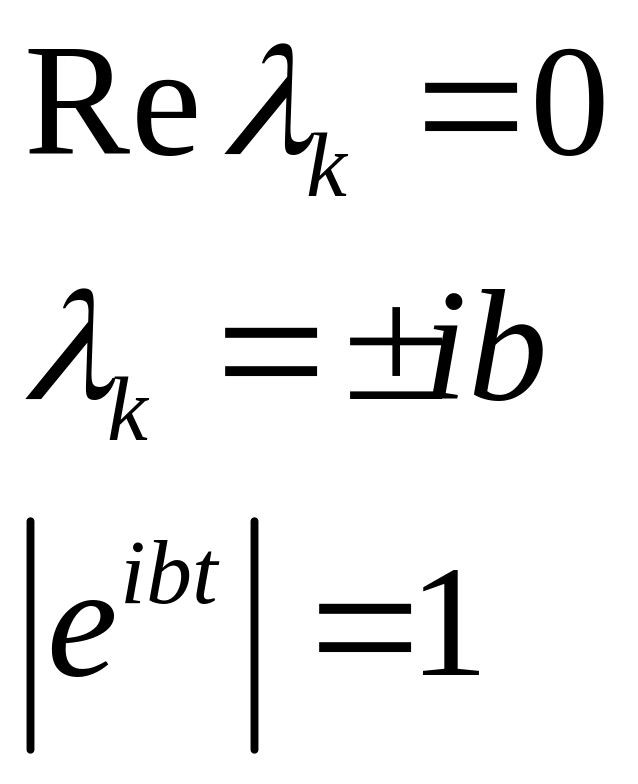
То решение
![]() не удаляется от положения равновесия,
то есть устойчиво по Ляпунову.
не удаляется от положения равновесия,
то есть устойчиво по Ляпунову.
![]() - не устойчиво
- не устойчиво
![]() при
при
![]() есть кратное.
есть кратное.
В разложении
матрицы
![]() есть экспонента от Жордановой клетки,
соответственно:
есть экспонента от Жордановой клетки,
соответственно:
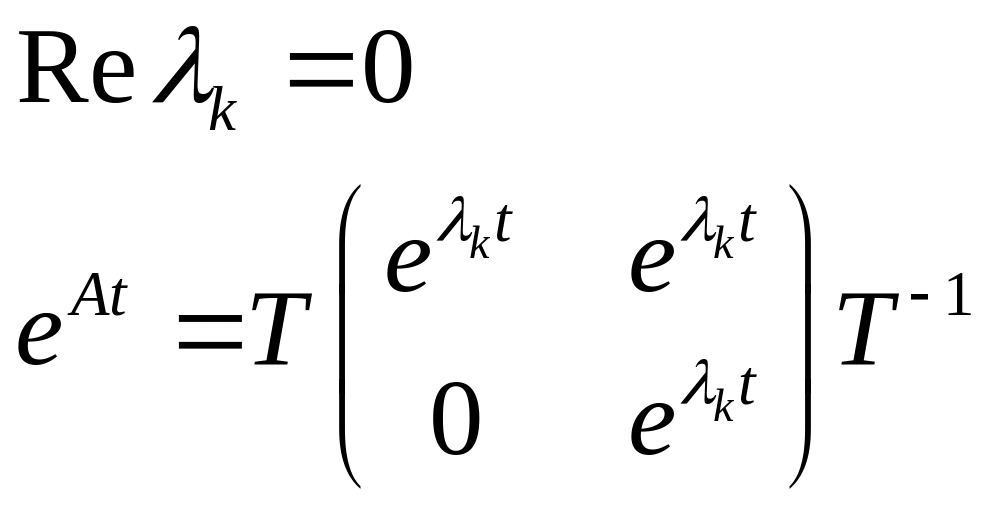
![]() -
-
Неограниченна, следовательно, нет никакой устойчивости.
Доказательство№2:
(с построение функции Ляпунова)
Построим функцию Ляпунова:
![]() над полем С
над полем С
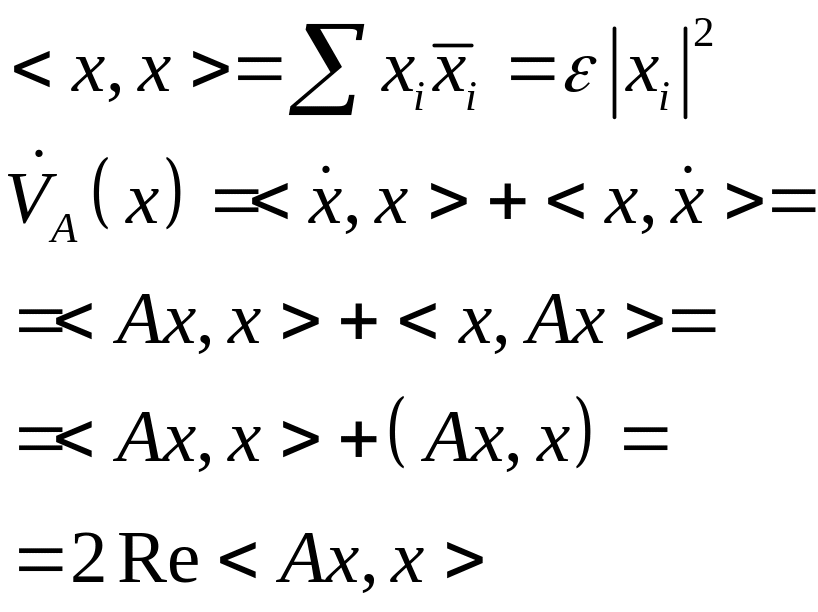
- тоже квадратичная форма (для устойчивости необходимо, чтобы форма была отрицательно-определенной)
Приведем матрицу
к Жорданову виду:
![]() где
где
![]()
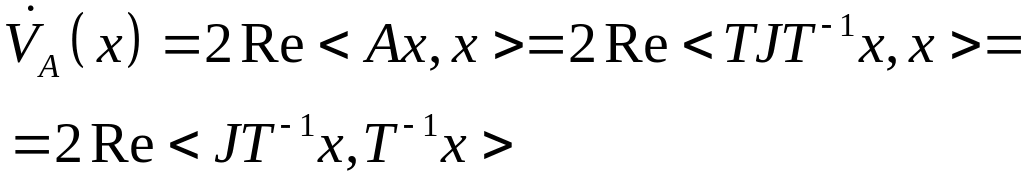
Перейдем к базису из собственных векторов:
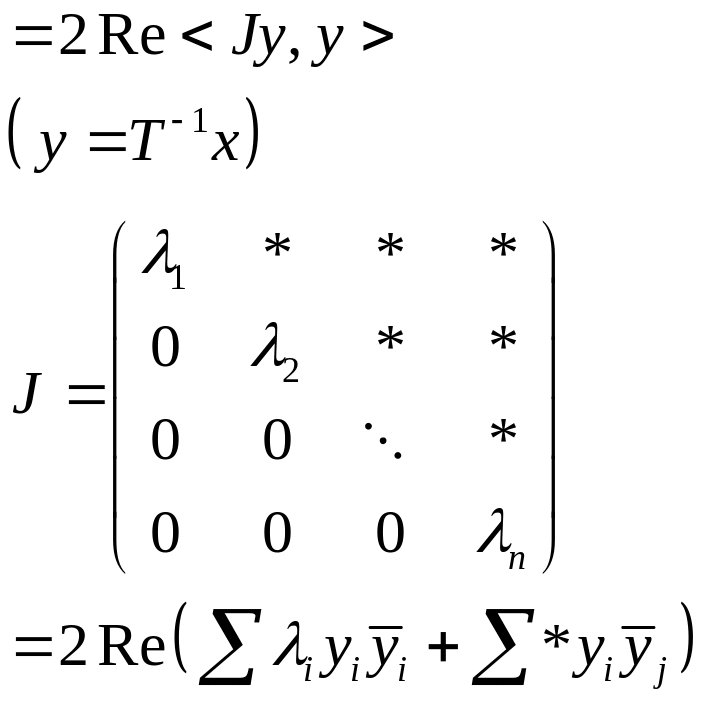
Лемма (о привидении матрицы к диагональному виду)
![]()
![]() - невырожденная,
- невырожденная,
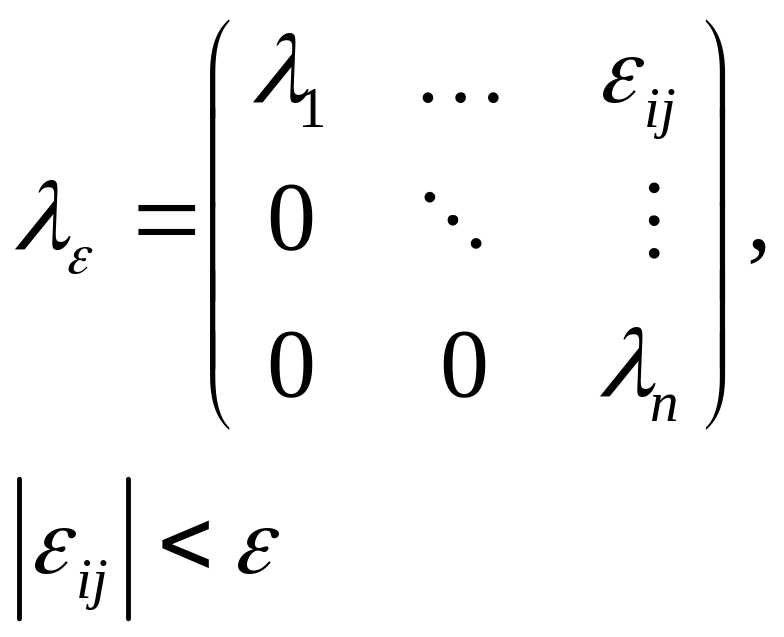
Доказательство:
Пусть привели матрицу А к Жорданову виду:
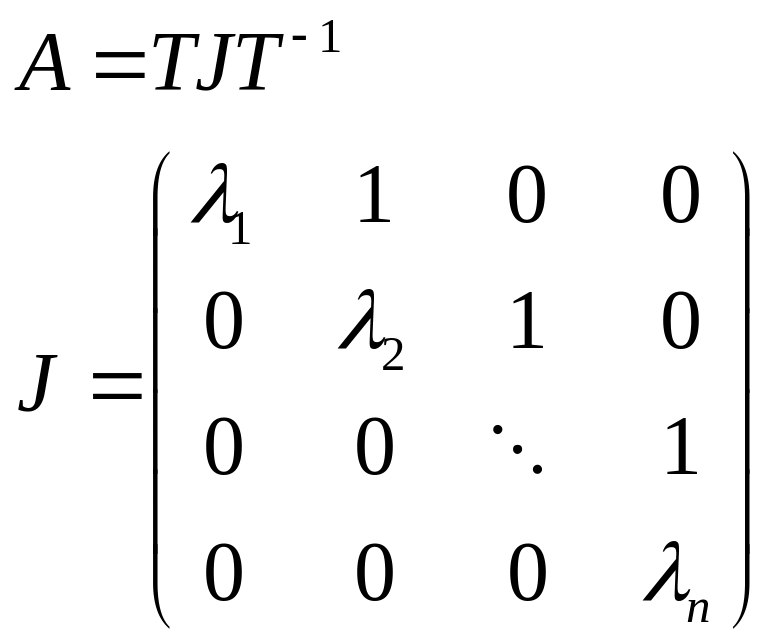
Выберем новый базис:
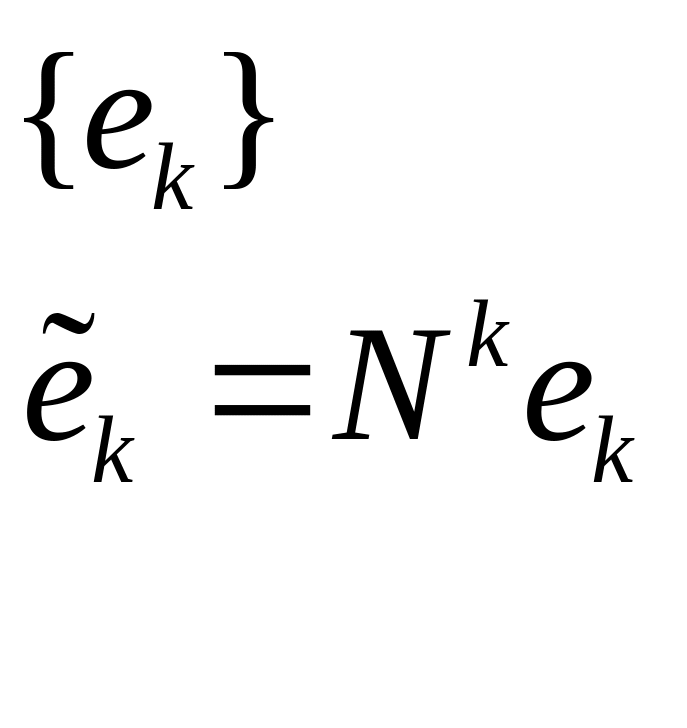
![]() - некоторое,
достаточно большое число
- некоторое,
достаточно большое число
![]()
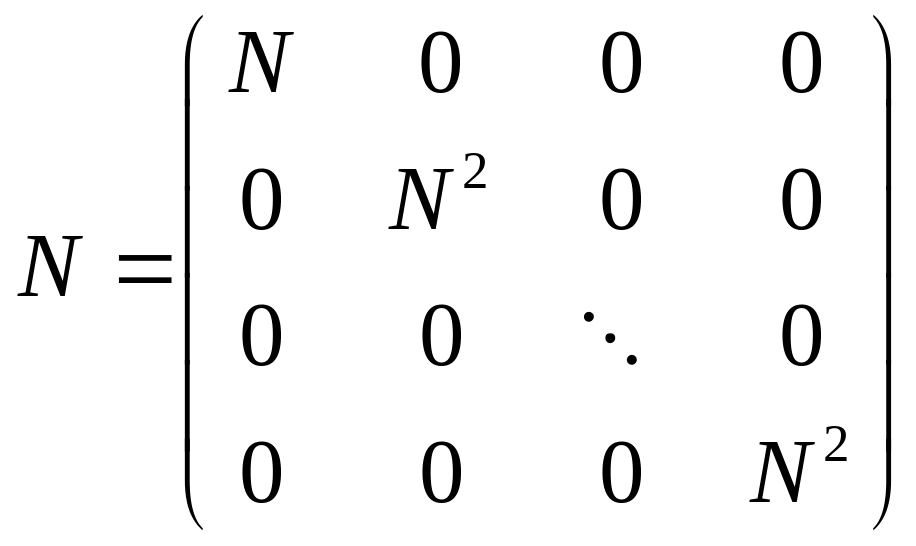 - матрица перехода
- матрица перехода
Преобразованная матрица:
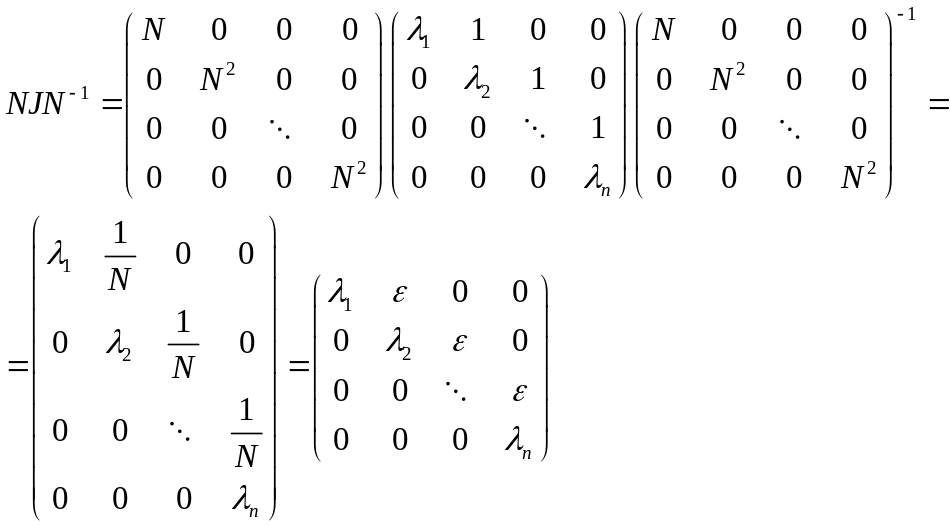
Продолжаем доказательство теоремы:
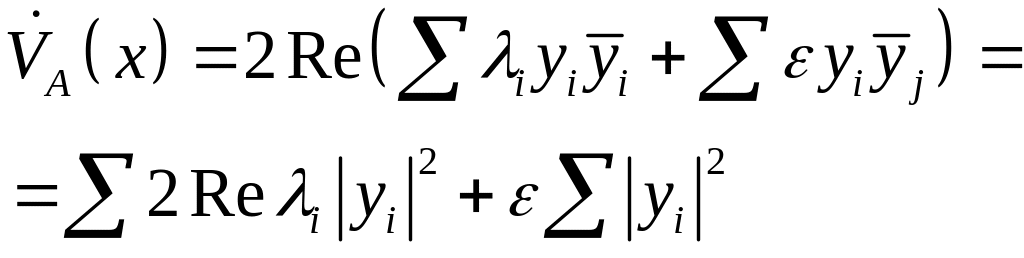
График
График
Если
![]() :
:
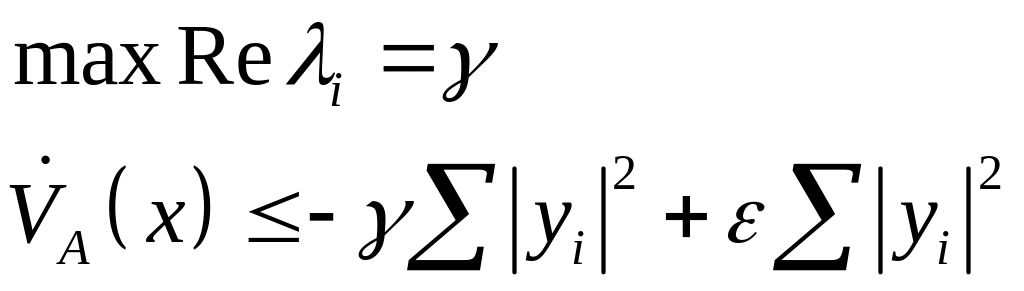
Выберем
![]() ,
тогда:
,
тогда:
![]()
Выполнены все условия теоремы Ляпунова Об асимптотической устойчивости.
Теорема об устойчивости по линейному приближению.
ВИКА!!!!!!
Следствие: если
![]() неустойчивость
неустойчивость
![]() ,
то
неустойчиво для исходной системы
,
то
неустойчиво для исходной системы
График
В случае чисто ??????? собственного значения теорема по линейному приближению не работает.
Доказательство (с построением функции Ляпунова):
![]()
В качестве функции Ляпунова возьмем:
- положительно-определенная
![]() - отрицательно-определенная
- отрицательно-определенная
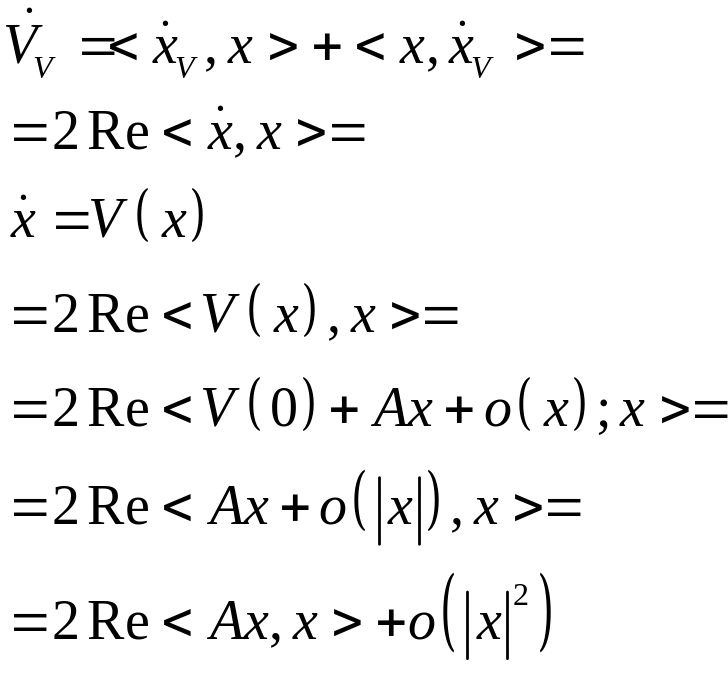
(по лемме из прошлой лекции)
Матрица А имеет
почти диагональный вид.
![]() можно переписать:
можно переписать:
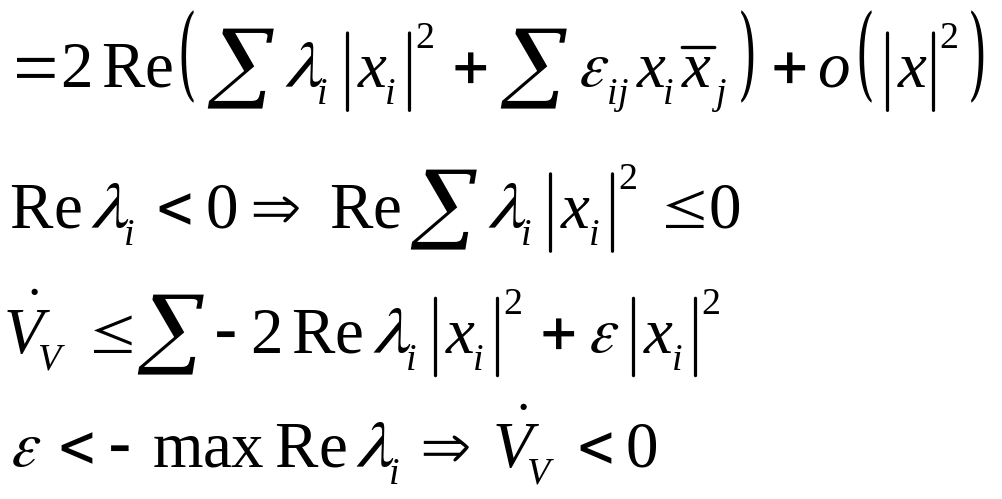
 отрицательно
определенная.
отрицательно
определенная.
Модель хищник жертва.
- жертва (отклонение от среднего)
![]() - хищник
- хищник
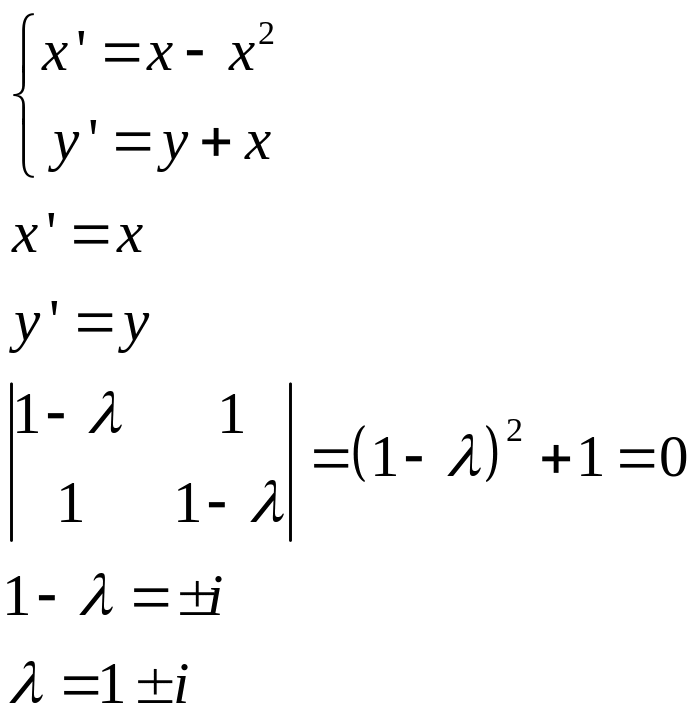
График
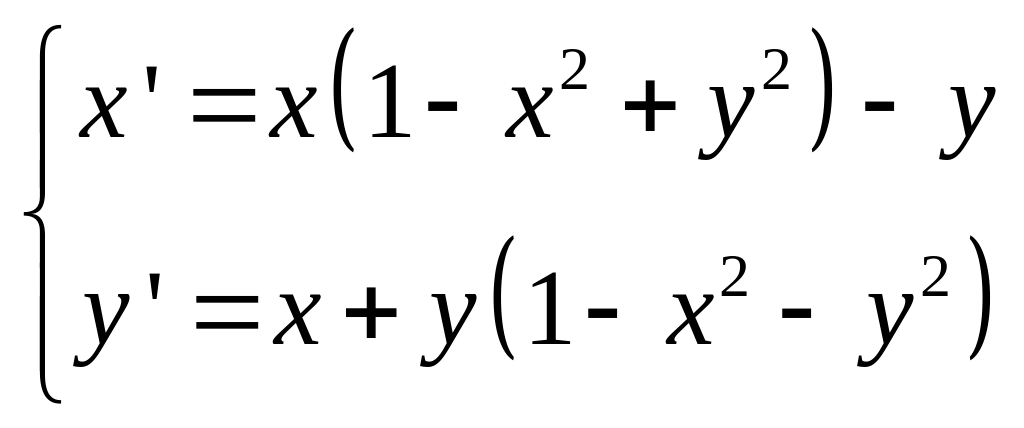
Перейдем к полярным координатам:

![]() - положение
равновесия
- положение
равновесия
График
неустойчивый фокус
График
Фазовая кривая
называется предельным циклом, если в
окрестности нет других предельных
циклов и любая другая фазовая кривая,
которая проходит через точку в некоторой
окрестности этого предельного цикла
приближается к нему неограниченно при
или
![]()
Если это приближение происходит при , то предельный цикл называется устойчивым, если при - неустойчивым.
Приложение к механике.
Закон Ньютона.
![]()
- координата,
![]() - сила,
- сила,
![]() - скорость,
- скорость,
![]() - расстояние,
- расстояние,
![]() - скорость,
- скорость,
тогда получим систему дифференциальных уравнений:
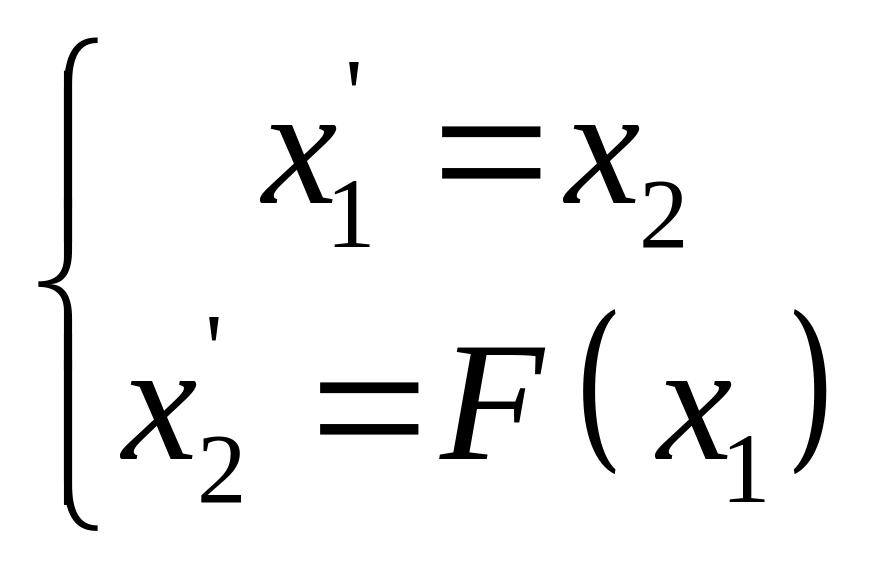
Кинетическая энергия:
![]()
 - потенциальная
энергия
- потенциальная
энергия
![]() - энергия (полная
энергия)
- энергия (полная
энергия)
Закон сохранения энергии.
При движении
по фазовой кривой:
![]()

Вывод: фазовые кривые не расходятся только на уровнях энергии.
График
Уравнение математического маятника.
![]()
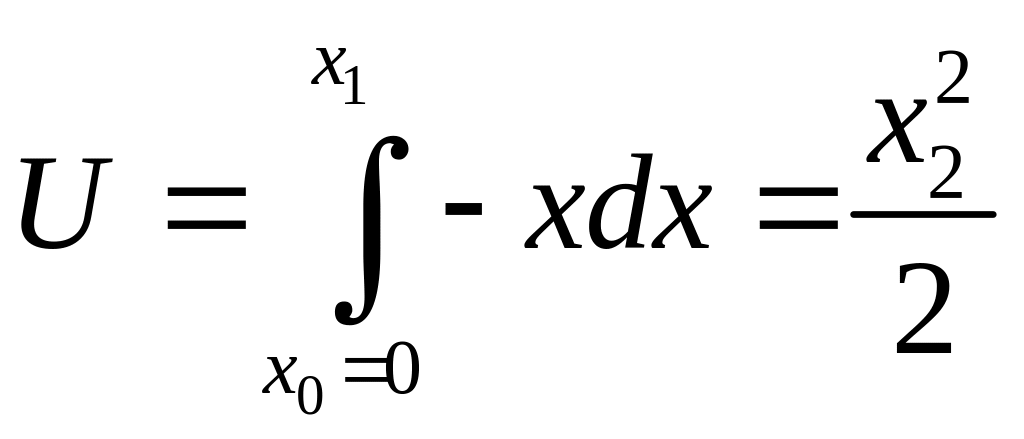 - потенциальная
энергия
- потенциальная
энергия
![]()
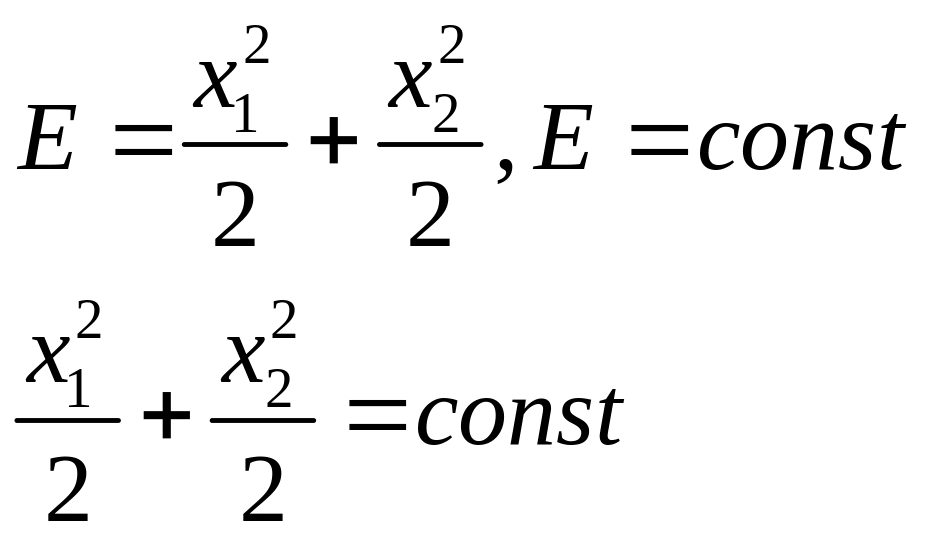
- линии уровня окружности
Линии энергии окружности
График
Уравнения перевернутого маятника.
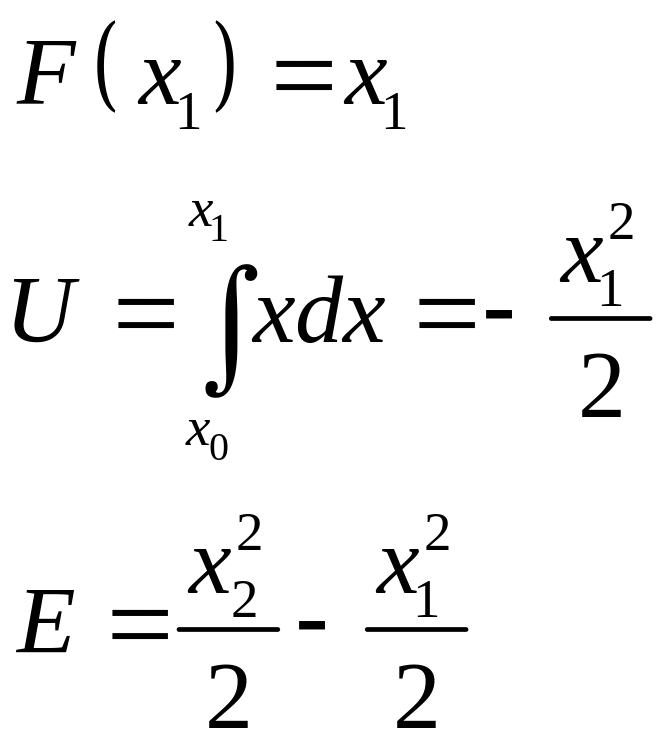
Линии уровня гиперболы.
График
Критические
точки для потенциальной энергии
![]() .
.
![]()
Критические точки полной энергии:
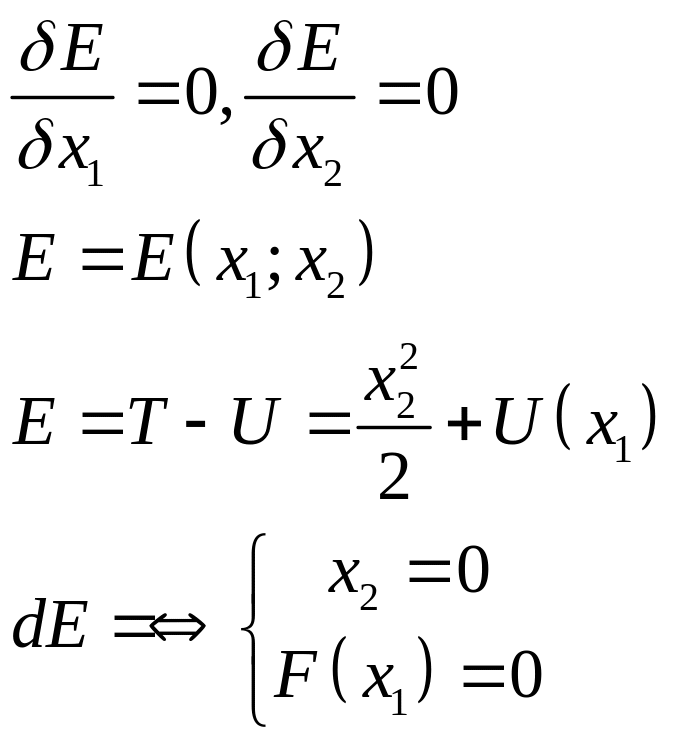
То есть точки полной энергии это как раз положение равновесия системы:
Полная энергия
![]() всегда больше потенциальной.
всегда больше потенциальной.
![]()
Если
![]() возрастает,
то
возрастает,
то
![]() убывает, если
убывает, то
возрастает.
убывает, если
убывает, то
возрастает.
График
График
Для того чтобы правильно строить линию уровня нужно исследовать критические точки потенциальной энергии.
Утверждение 1.
Если
![]() ,
то линии уровня:
,
то линии уровня:
![]() гиперболы
гиперболы
![]() эллипсы
эллипсы
Утверждение 2.
Если уровень энергии не совпадает с критическим, то линия уровня гладкая кривая
![]() - критическая
- критическая
![]() ,
то
,
то
![]() критический уровень энергии.
критический уровень энергии.
Доказательство:
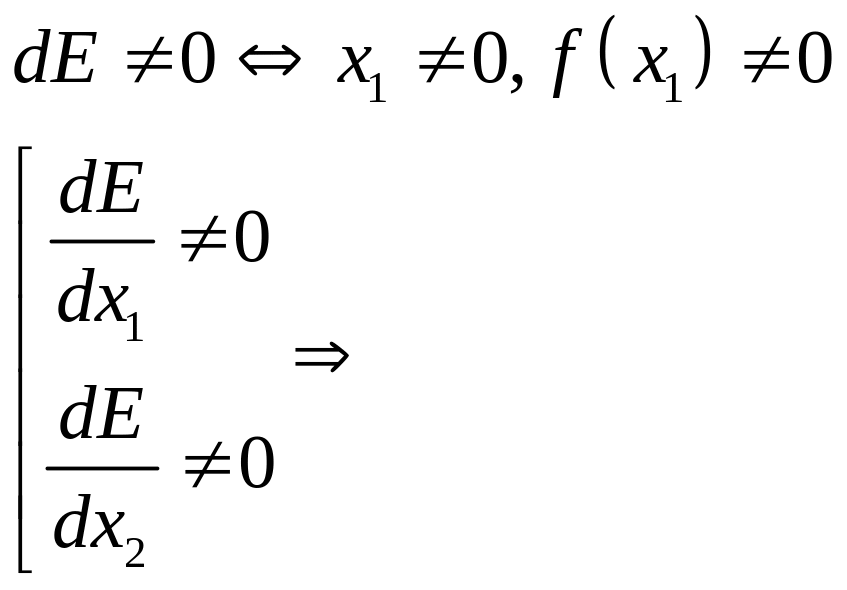
По теореме о
неявной функции из равенства
![]() выражаем одну из переменных через другую
(гладким образом)
выражаем одну из переменных через другую
(гладким образом)
Лемма.
Пусть
- невырожденная критическая точка
функции
![]() ,
,
![]() ,
,
![]() ,
тогда существует гладкая замена
координат, в которой приращение функции
имеет квадратичный вид
,
тогда существует гладкая замена
координат, в которой приращение функции
имеет квадратичный вид
![]()
Доказательство:
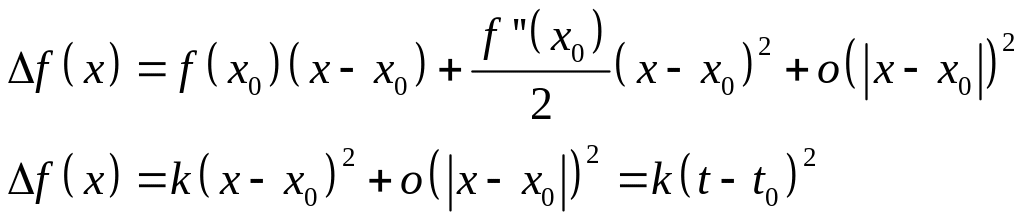
Следствие.
В окрестностях критических точек потенциальной энергии линии уровня диффеаморфны,!!!! Либо эллипсам, либо гипереболам.
Утверждение 3.
Если значение энергии не совпадает с критическим значением энергии, тогда линии уровня состоят из конечного счетного числа замкнутых гладких кривых и не более чем двух гладких (незамкнутых) кривых
Доказательство:
График
Рассмотрим
множество
,
что
![]() поскольку
поскольку
![]() - непрерывная, то это множество состоит
из не более чем счетного количества
отрезков
- непрерывная, то это множество состоит
из не более чем счетного количества
отрезков
![]()
![]()
![]()
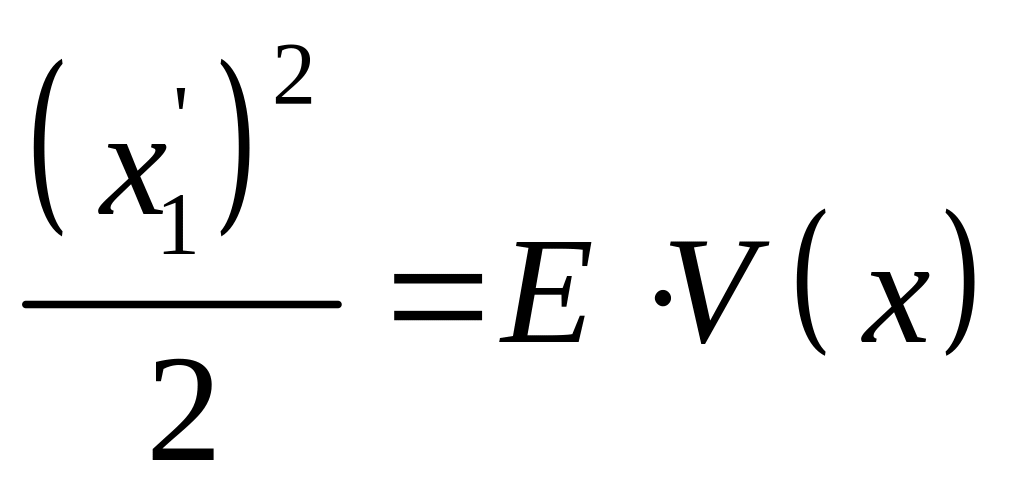
![]() - уравнение с
разделяющимися переменными
- уравнение с
разделяющимися переменными
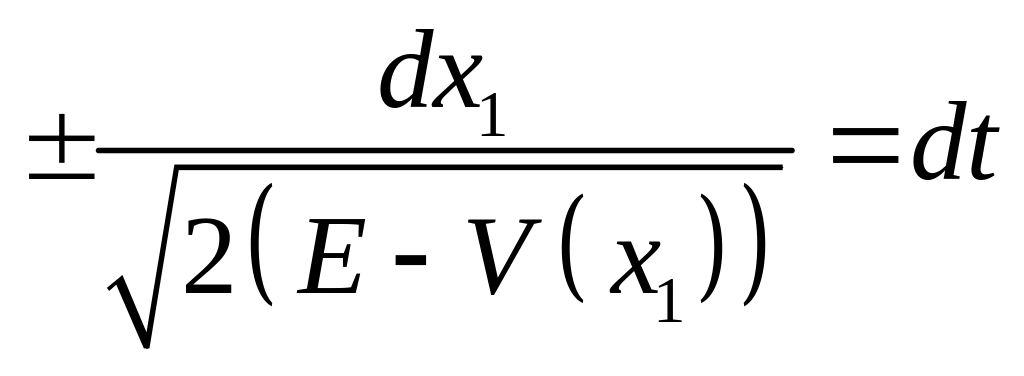
Проинтегрируем
от
![]() до
до![]()
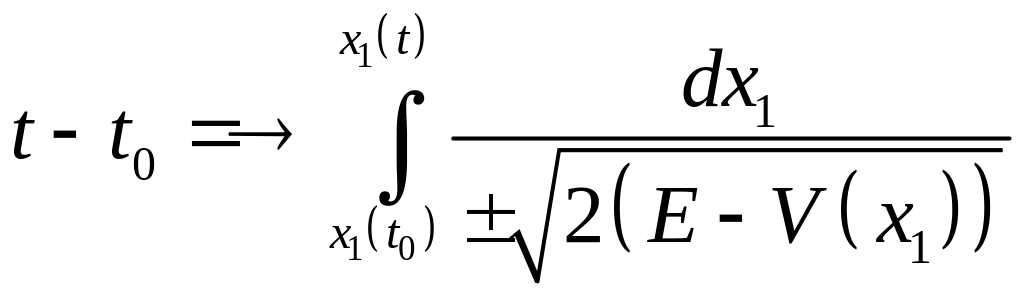
найдено но не в
явном виде. Приблизим
к точке![]() (не является критическим значением,
интеграл сходится)
(не является критическим значением,
интеграл сходится)
![]()
![]()
Раз сходится
интеграл то в левой части
![]() тоже конечно и значит линии уровнясостоят
всего из 1-ой кривой
тоже конечно и значит линии уровнясостоят
всего из 1-ой кривой
График
По этому на линии уровня укладывается ровно одна фазовая кривая. Причем для отрезков получаем периодичные фазовые кривые (циклы). Лучу соответствует незамкнутая фазовая кривая.
Значения энергии совпадают с критическими значениями потенциальной энергии.
График
График
Надо выяснить,
что происходит когда
![]() .
.
Рассмотрим:
![]()
Фазовая кривая подходит к точке за бесконечно время или уходит за бесконечно время.
График
График
Элементы аналитической теории дифференциальных уравнений.
- аналетична в окрестности точки . Если раскладывается в ряд:
![]()
если
![]()
![]()
аналетична, следовательно, и аналетична ее производная на:
![]()
Теорема
Пусть
![]() ,
где
,
где
![]() - аналетические, тогда решение этого
уравнения тоже аналетично.
- аналетические, тогда решение этого
уравнения тоже аналетично.
Доказательство
Разложим в ряды
![]()
![]()
![]()
Решение (если существует аналетическое решение) имеет вид:
![]()
![]()
Прировняем коэффициенты при одинаковой степени - получим какие-то алгебраические уравнения. Из этих уравнений последовательно найдем коэффициенты.
![]()
![]()
Первые коэффициенты мы можем задатьпроизвольно
![]()
![]()
Пример:
![]()
![]()
![]()
Обозначим
![]()
![]()
![]()
![]()
![]()
![]()
………………………
![]()
![]()
![]()
![]()
![]()
![]()
Другая задача Коши:
![]()
![]()
![]()
![]()
Общее решение:
![]()
Особые точки
![]()
Уравнение Эйлера
