Определение

Пусть функция двух переменных будет квазеоднородной, если для некоторых и и для выполняется

Некоторые уравнения сводятся к однородным при помощи замены

Пример

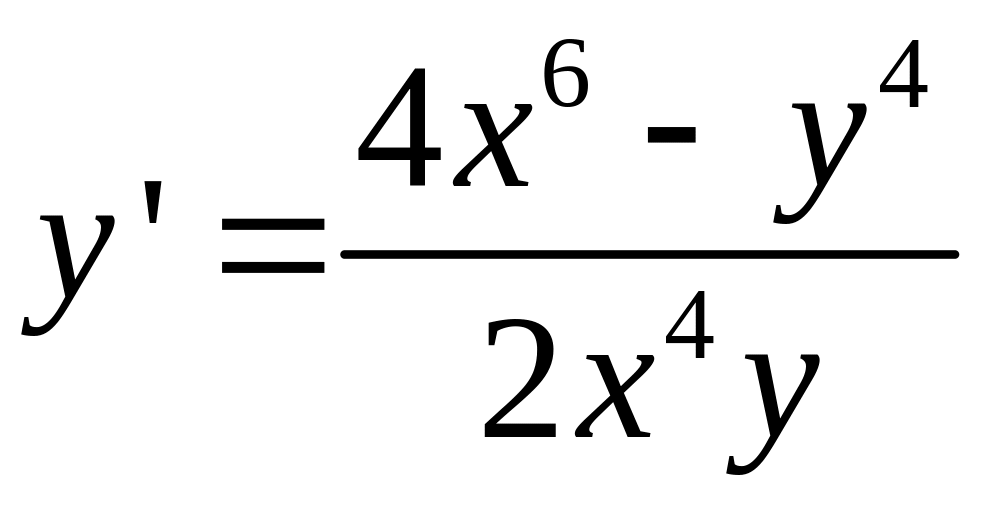- неоднородное уравнение.

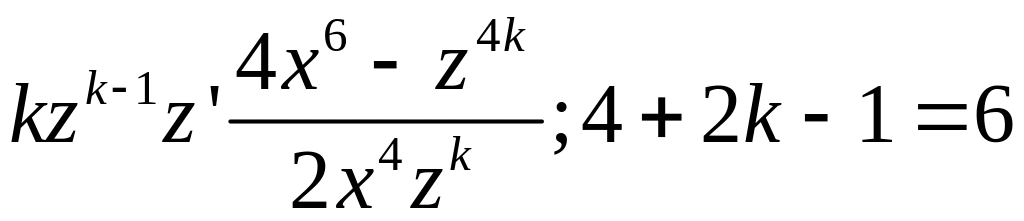
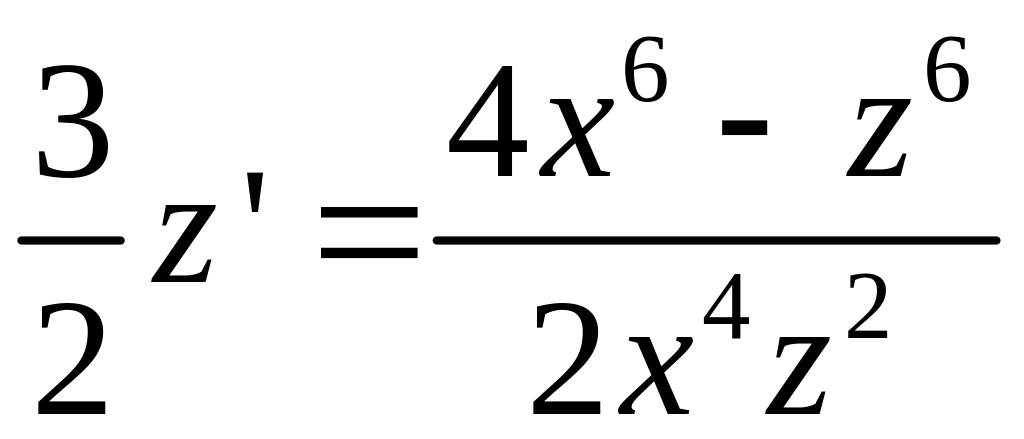
5. Линейные уравнения

Дифференциальным называется уравнение если:

(ЛУ)

(ЛОУ)

Линейные однородные уравнения.

Линейное отображение в линейном пространстве Х

A – линейное отображение

Линейное отображение (оператор)

Задано на линейном пространстве дифференциальных функций.

- переводит сумму в сумму

Ядро линейного отображения

Образ линейного отображения

Решить ЛОУ

Найти

Множество решений ЛОУ само является линейным пространством, то пространство одномерно.

- решение, все остальные имеют вид

Для ЛУ:

Решение представлено в виде:

- два решения ЛУ

то - решения ЛОУ

6. Нахождение частного решения оу Метод Бернулли

Ищем решение в виде

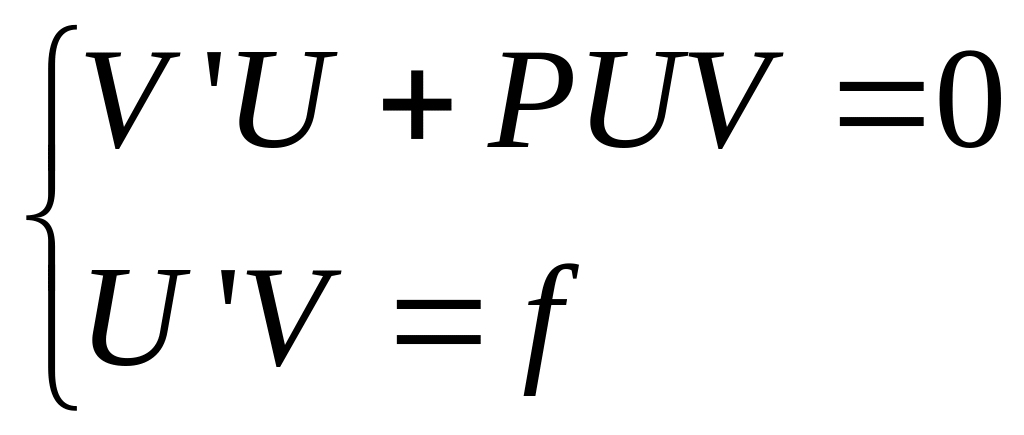
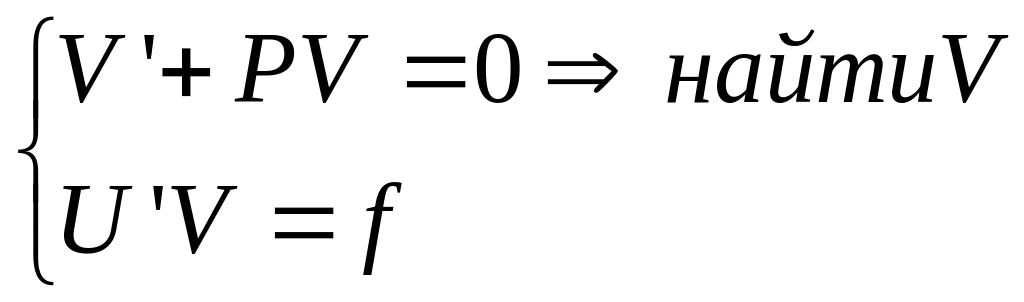
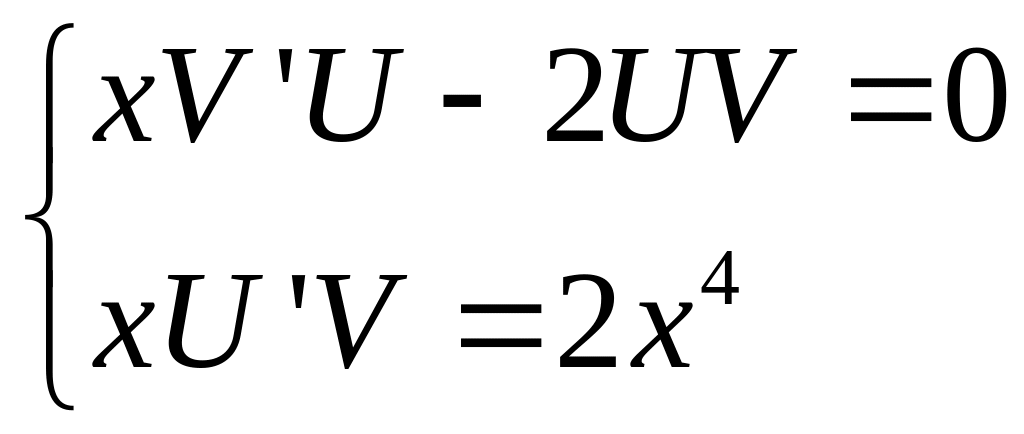
- в квадратурах.

Уравнение Бернулли

Метод Бернулли решает это уравнение

Уравнение Риккати

Если у уравнения Риккати найти случайно (подбором) какое-нибудь частное решение, тогда общее решение можно вычислить при помощи подстановки

- частное известно.

Применив такую подстановку, получим уравнение Бернулли.

7. Задачи

1. Сосуд содержит 10 литров воды. Непрерывно поступает раствор со скоростью 2л/мин, в каждом литре которого содержится 0,3 кг. Соли. Он перемешивается и раствор вытекает с той же скоростью. Сколько соли будет в сосуде через 5 минут?

Решение.

Определим t – время.

Затем у(t) – неизвестная функция в данном случае, как изменяется за

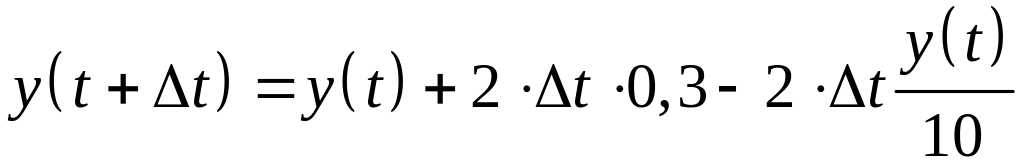
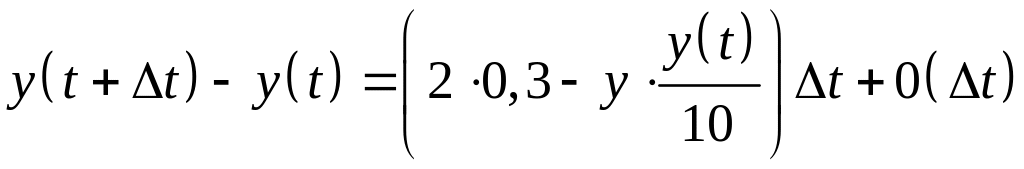
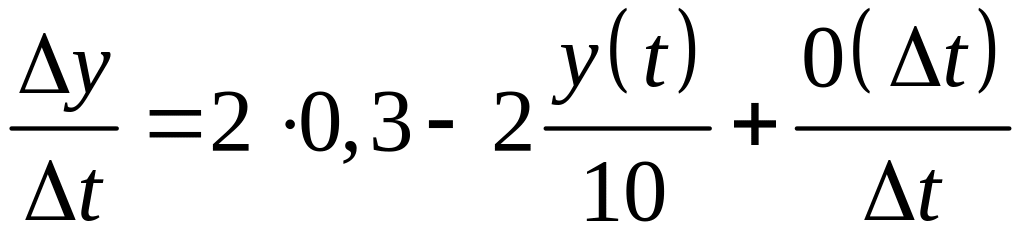
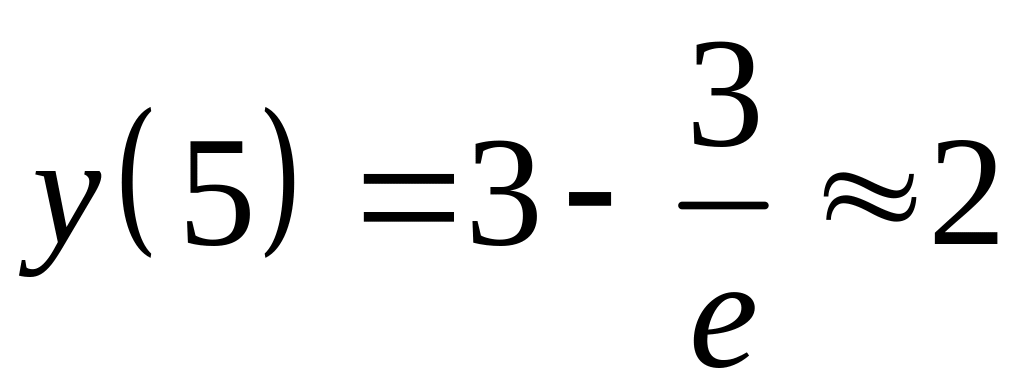
- уравнение Риккати

1. Подбор решения

2. Замена

- уравнение Бернулли.

3. Метод Бернулли

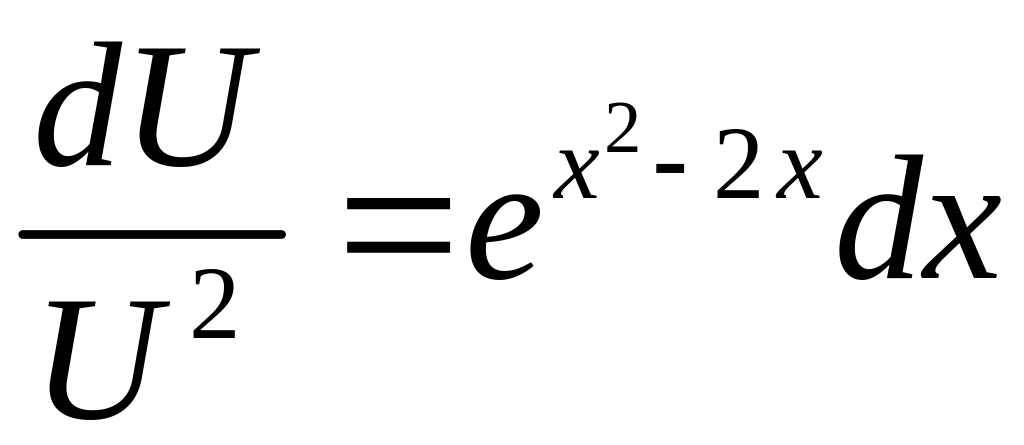
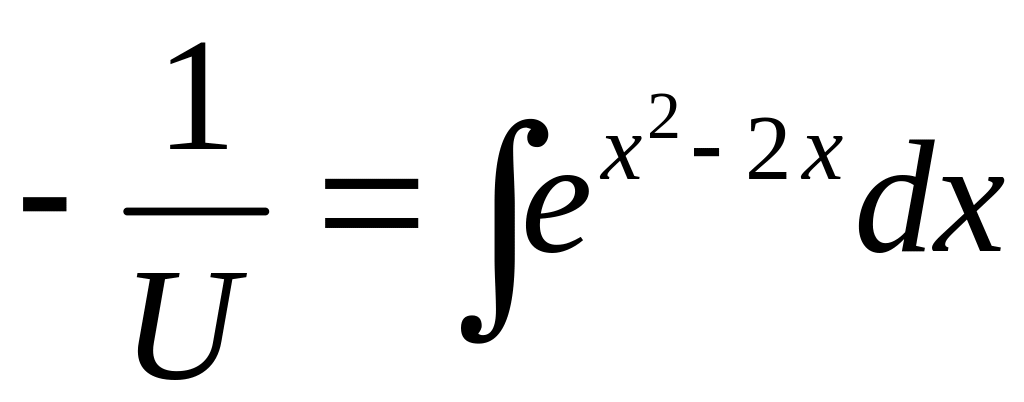
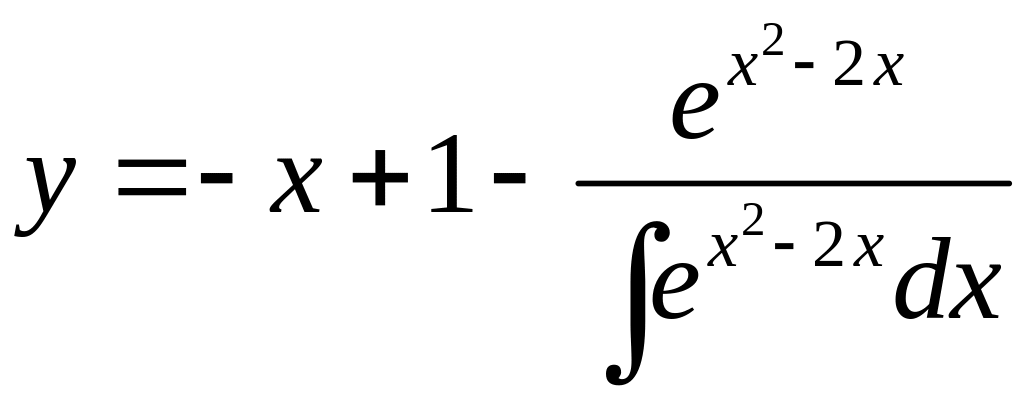
8. Уравнения в полных дифференциалах

Определение

Уравнение называется уравнением в полных дифференциалах, если левая часть является дифференциалом функции двух переменных

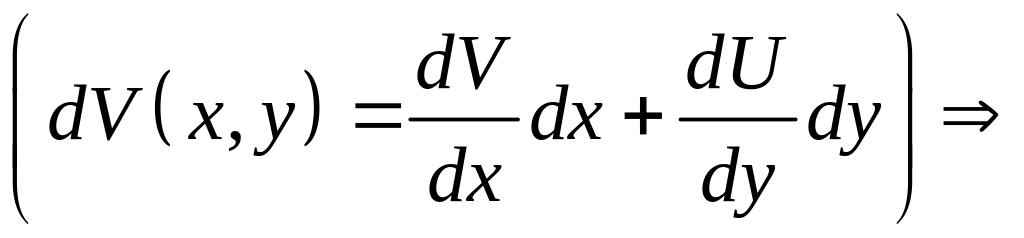
в этом случае

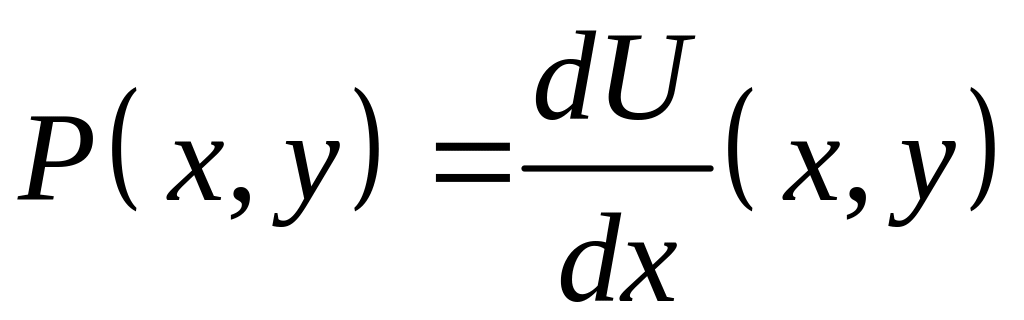
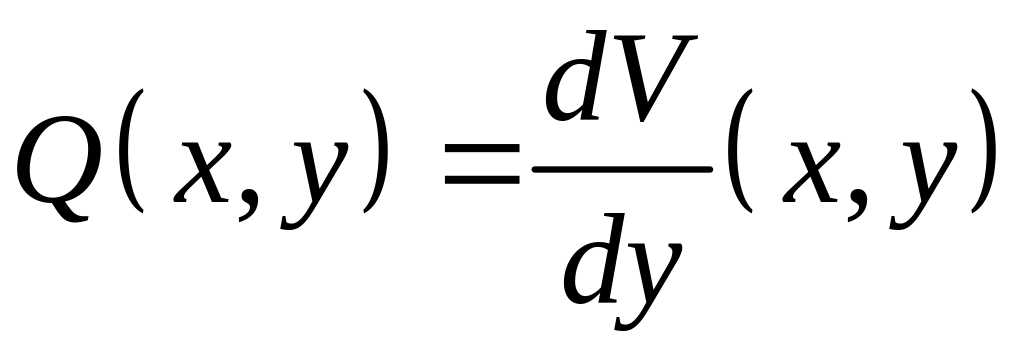
если известно

- общее решение.

Задача найти - потенциал.

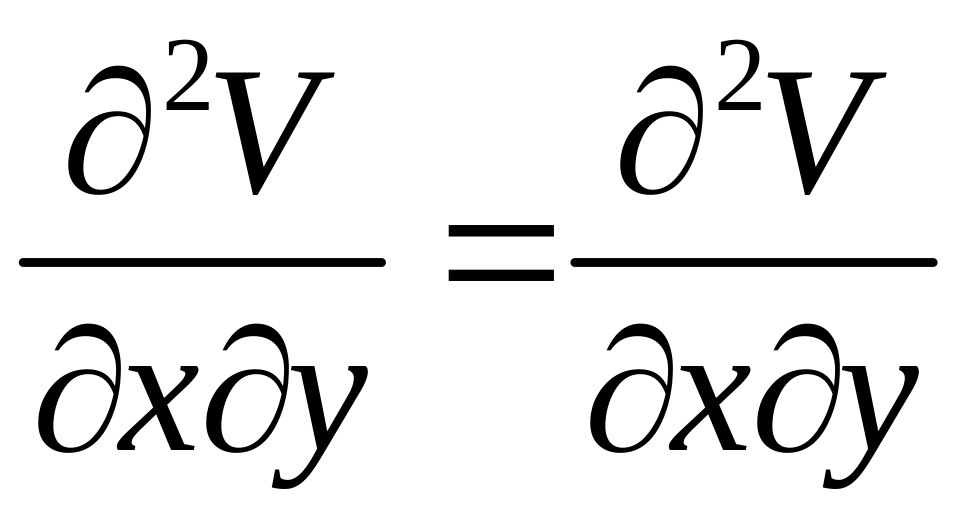
1. Необходимое условие уравнения в полных дифференциалах:

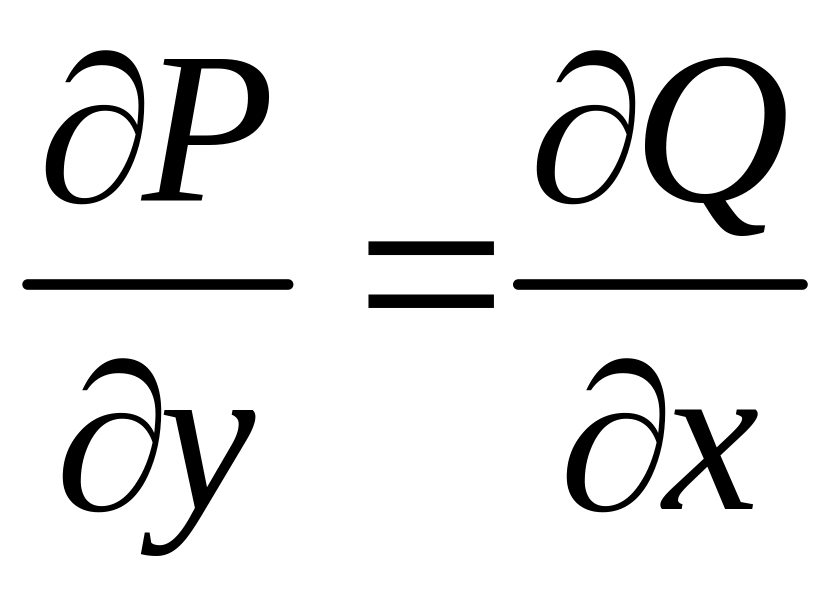
2. В односвязной области это условие достаточно:

Как найти V, зная

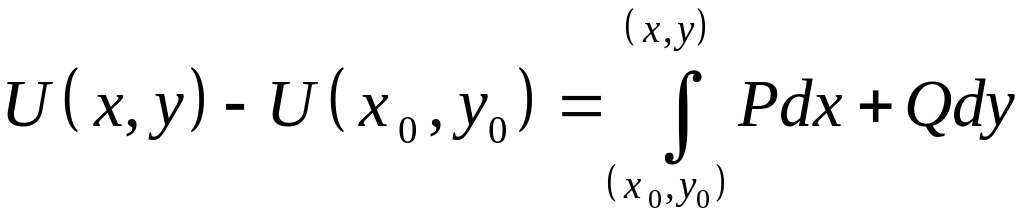
На практике поступаем так:

- неизвестное

Проверка

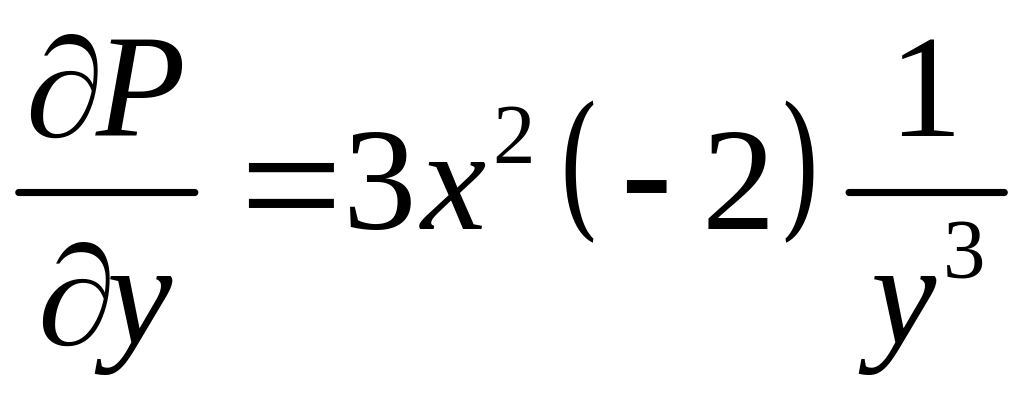
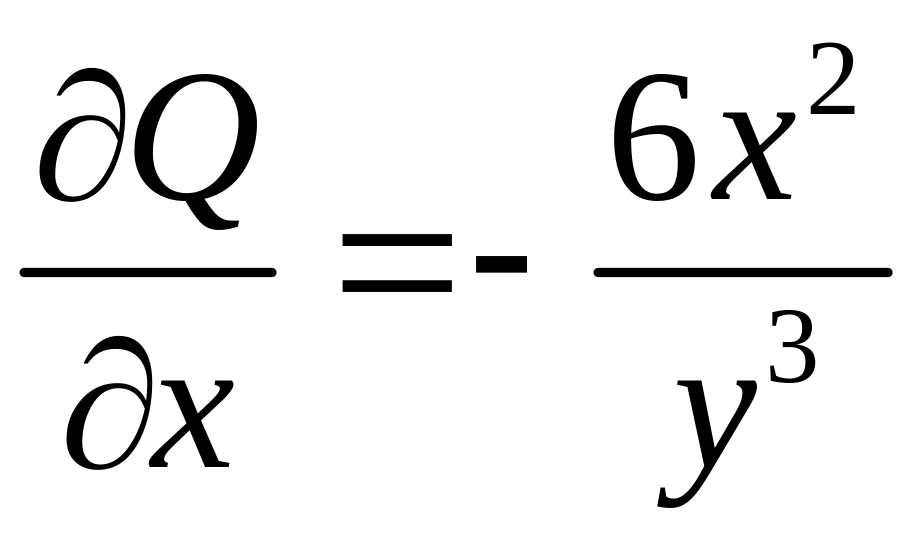
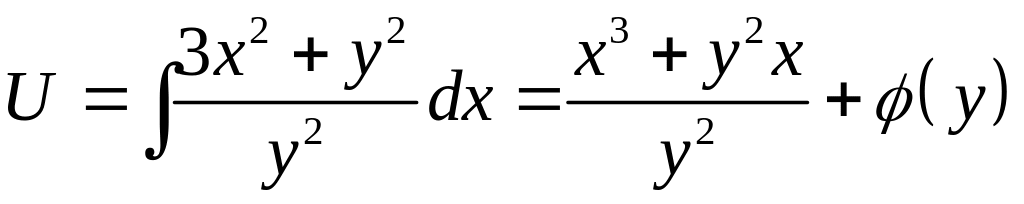
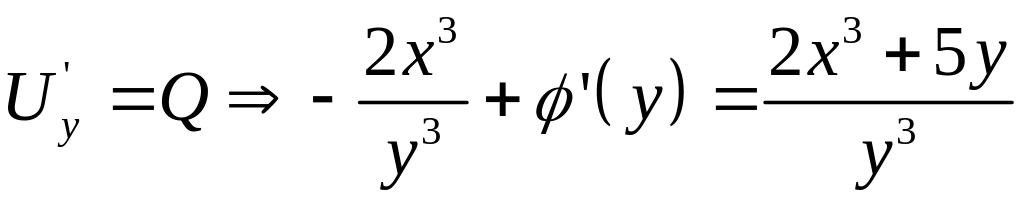
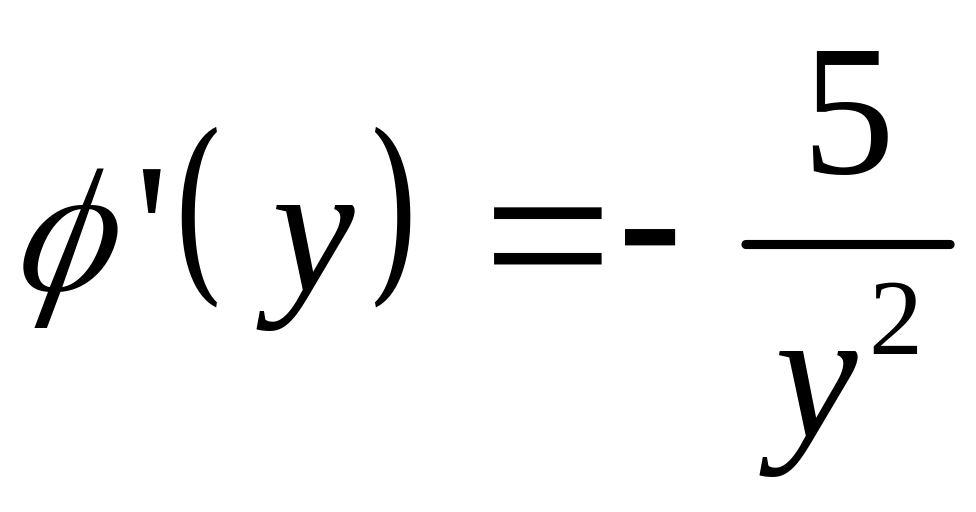
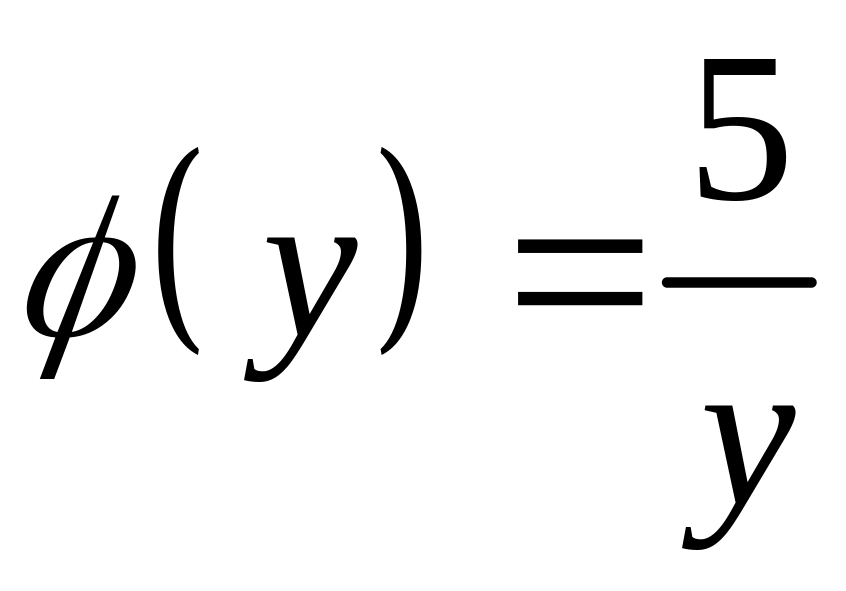
Ответ: потенциал.

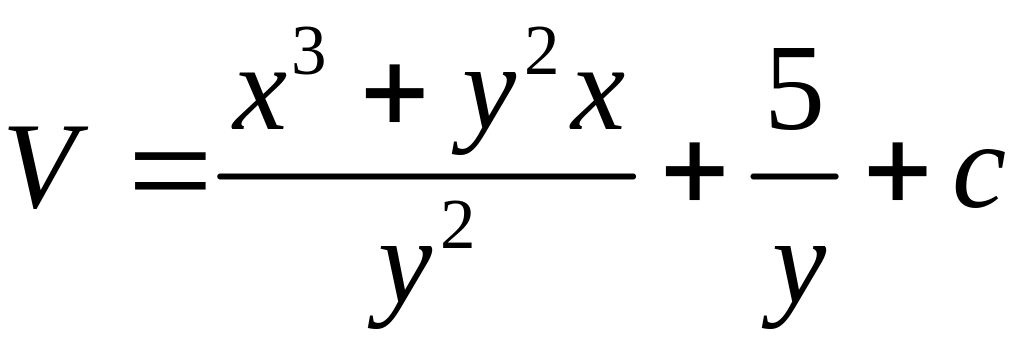
Общее решение

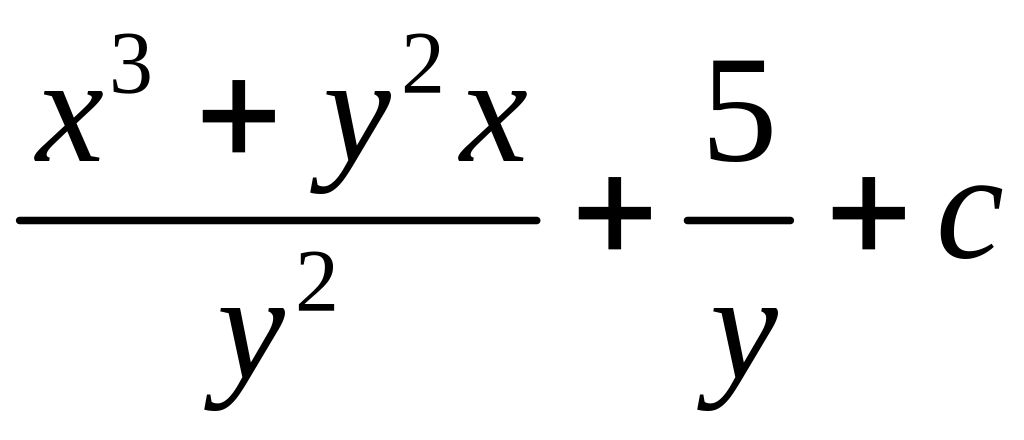
9. Интегрирующий множитель

Если , что при умножении на нее уравнение станет уравнением в полных дифференциалах, то - интегральный множитель.

Уравнение относительно - сложное уравнение в частных производных. Бывает так, что зависит только от одной переменной, тогда он легко находится.

10. Интегрирующие комбинации

Можно разрывать уравнение на части, находя интегрирующие комбинации.

1)

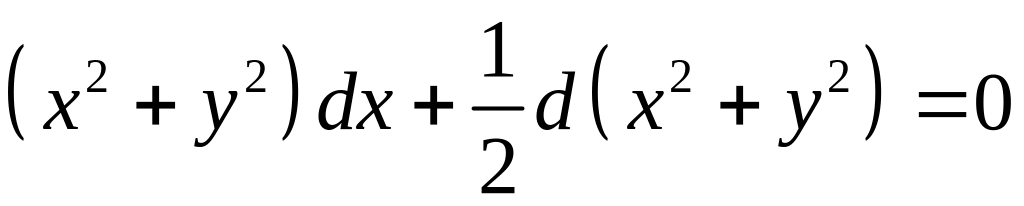
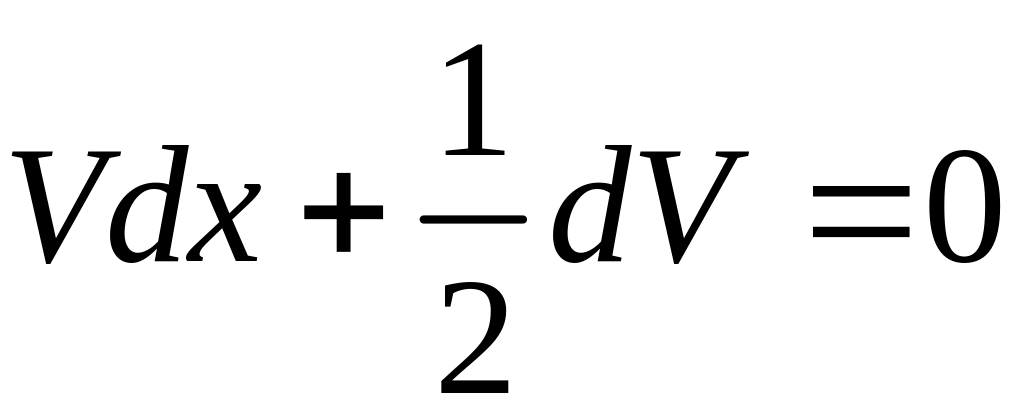
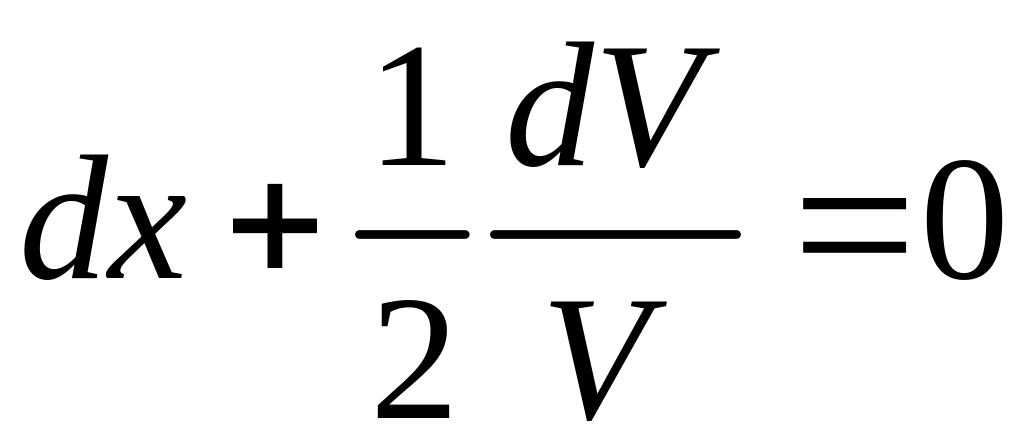
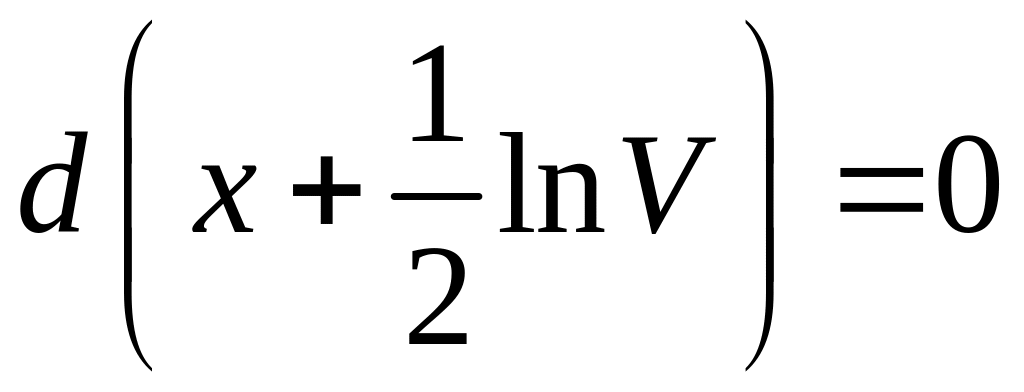
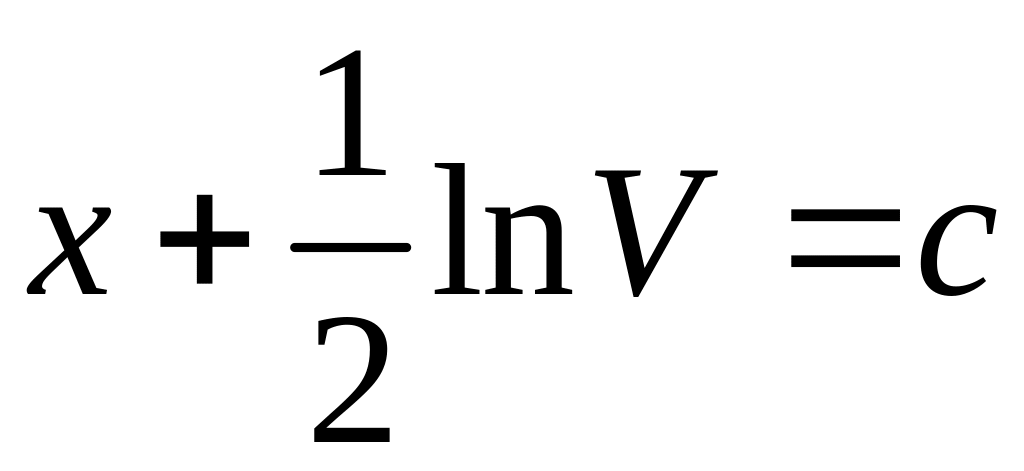
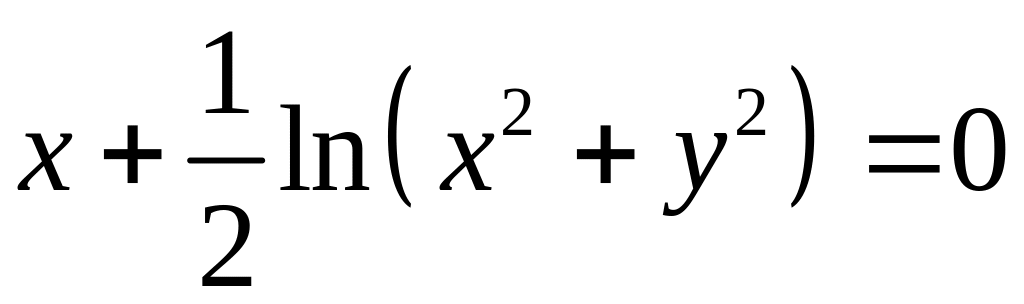- общее решение

2)

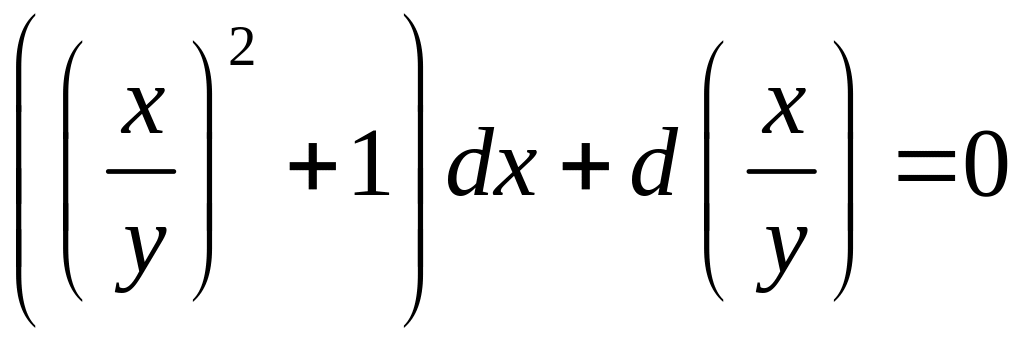
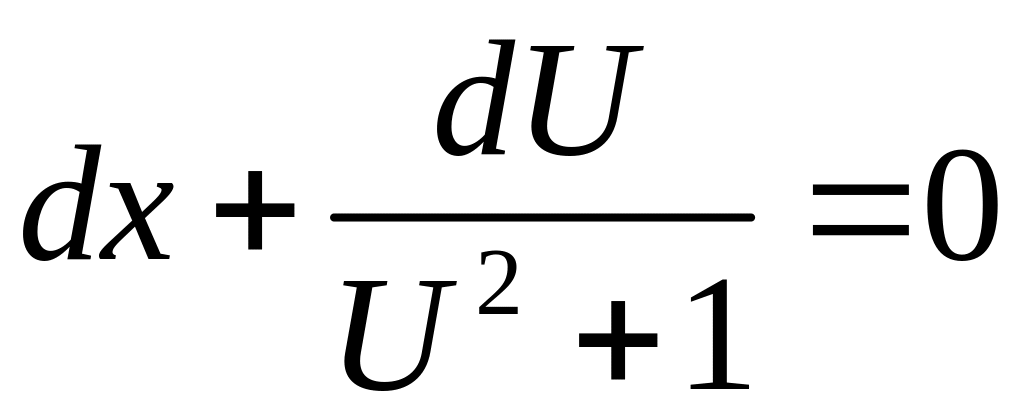
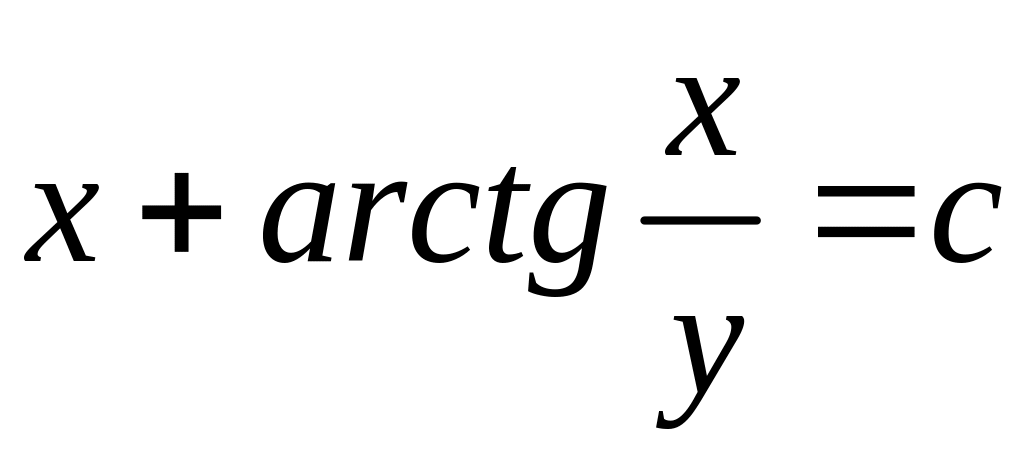
3)

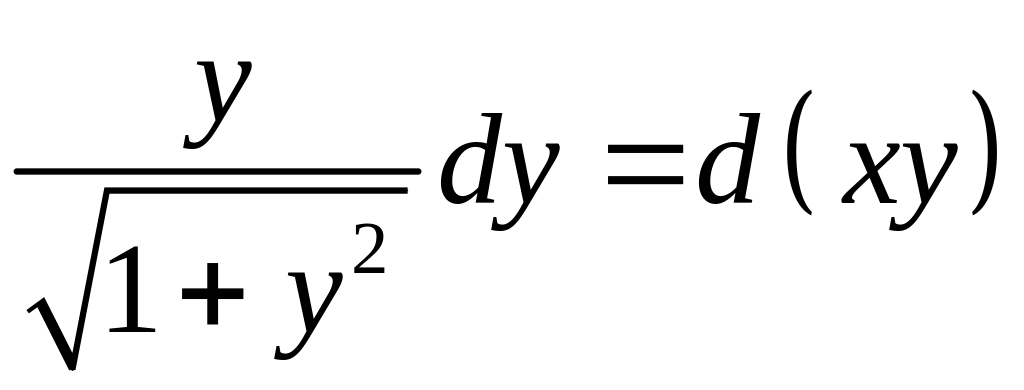
4)

Проверить, что в полных дифференциалах

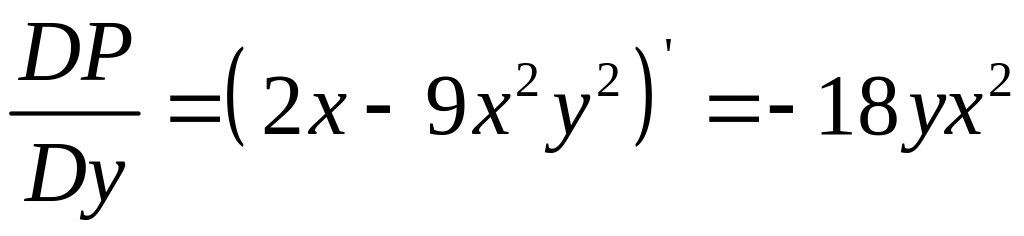
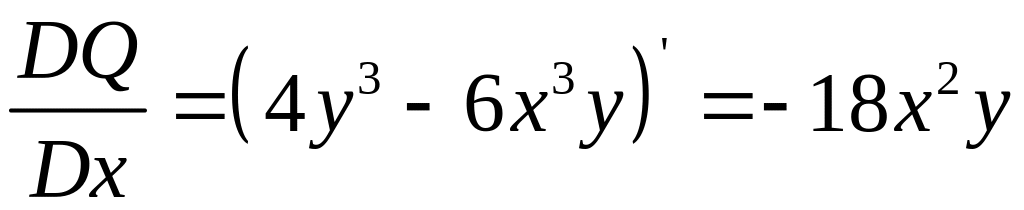
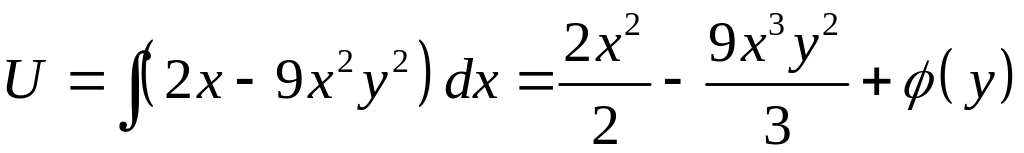
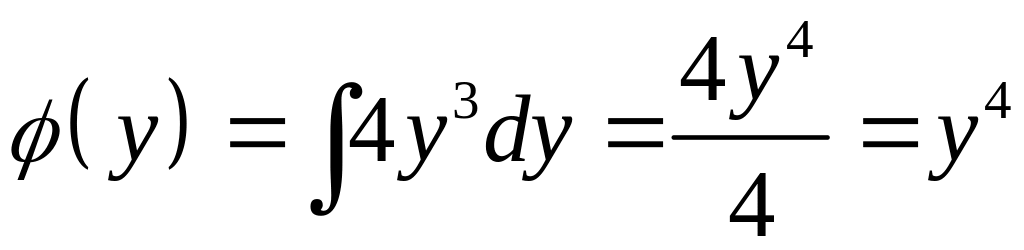
Потенциал:

11. Уравнения, не разрешенные относительно производной

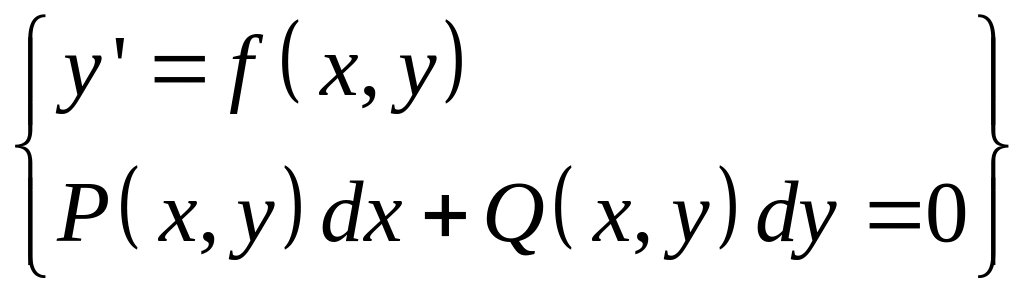- нормальный вид

- уравнение общего вида

Для этих уравнений может быть нарушено ТСЕ (теорема о существовании и единственности)

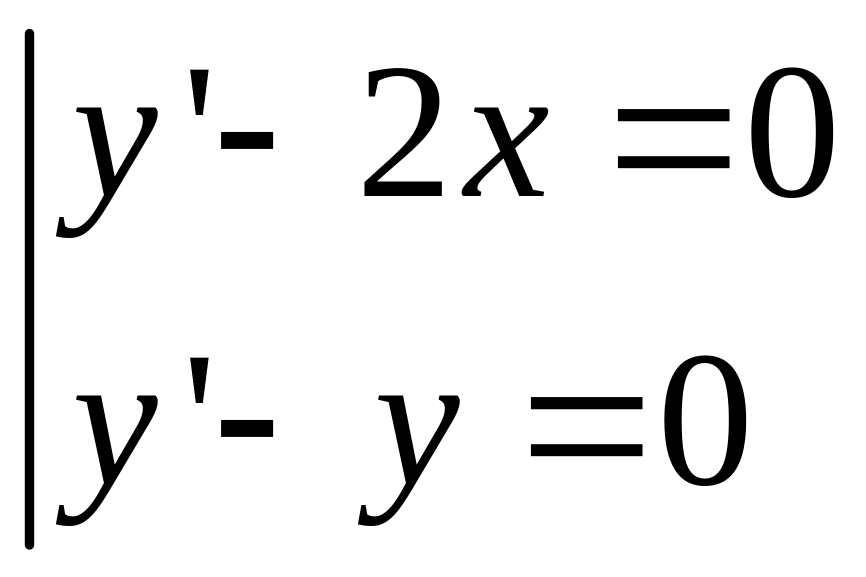– ТСЕ

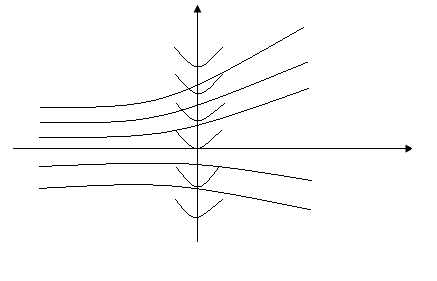
Функция F раскладывается в совокупность двух простых уравнений, для каждого из которых выполняется ТСЕ.

В общем случае нарушение ТСЕ может привести к особым решениям.

Определение

Решение называется особым, если в каждой его точке нарушается единственность решения

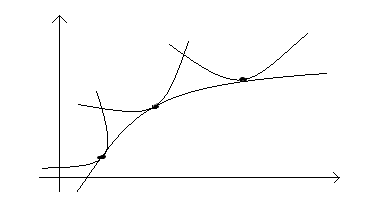
Через каждую точку данного решения проходит еще одна отличная от данной интегральная кривая.

12. Особое решение, его поиск (частный случай).

Пример

а) Рассмотрим тогда через каждую точку проходит решение (ТСЕ).

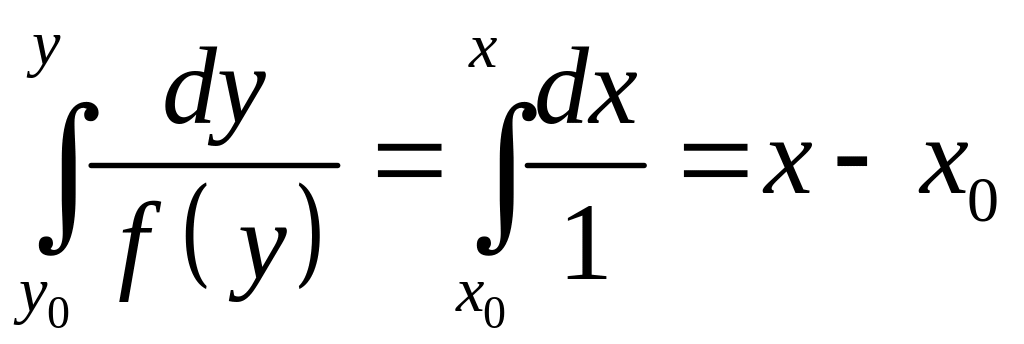
Это уравнение неявно задает функцию у от х (или х от у).

б) Рассмотрим

Берем функцию - решение.

Необходимо выяснить является ли решение , особым.

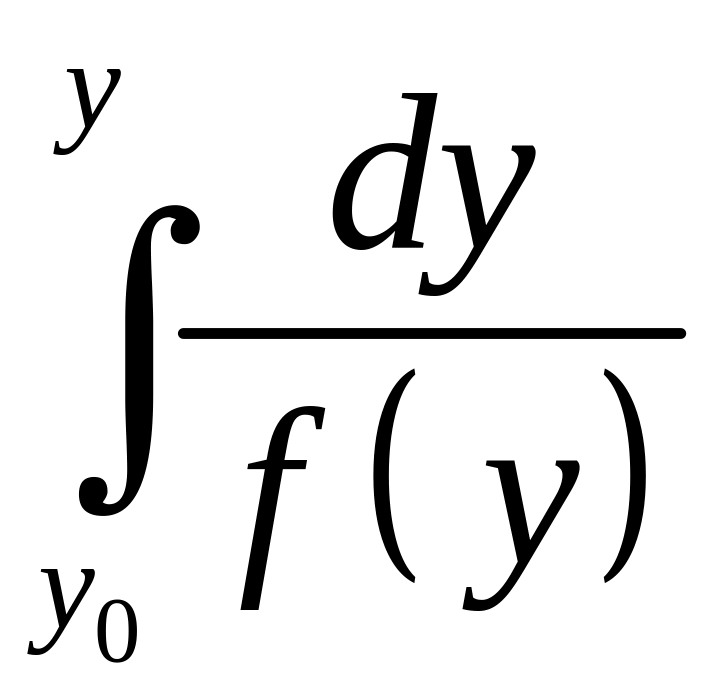- несобственный интеграл, так как

Если этот интеграл расходится, то особого решения не будет.

Пример.

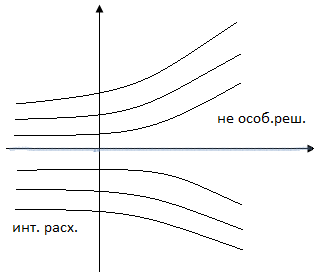
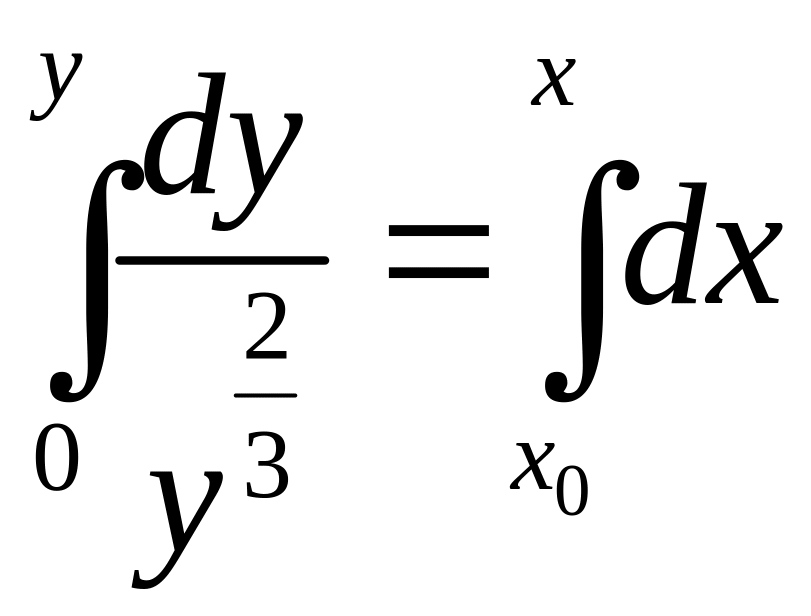
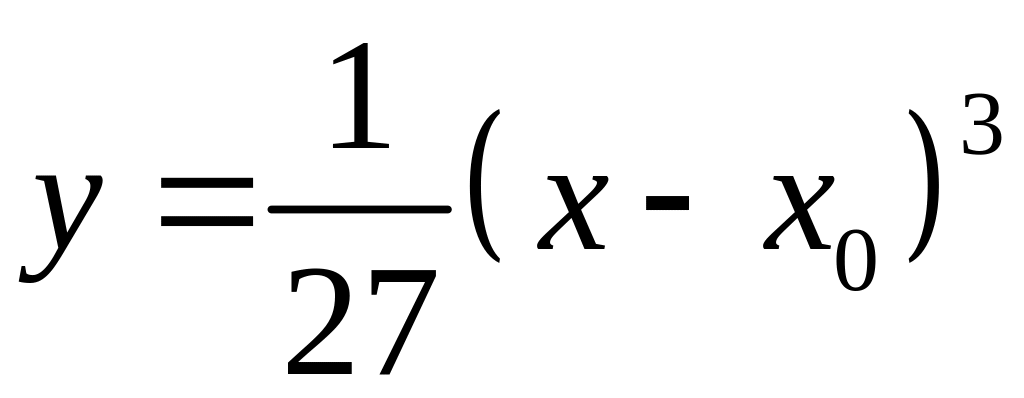
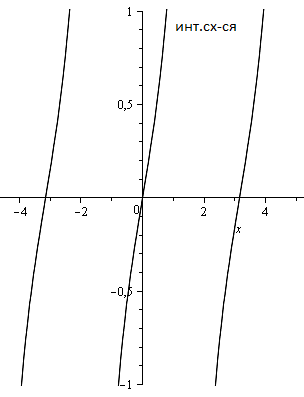
Решения подозрительные на особые (в общем случае)

Если непрерывны, то нет особых решений.

По теореме о неявной функции можно: 1) выразить через х и у; 2) найти ее частные производные

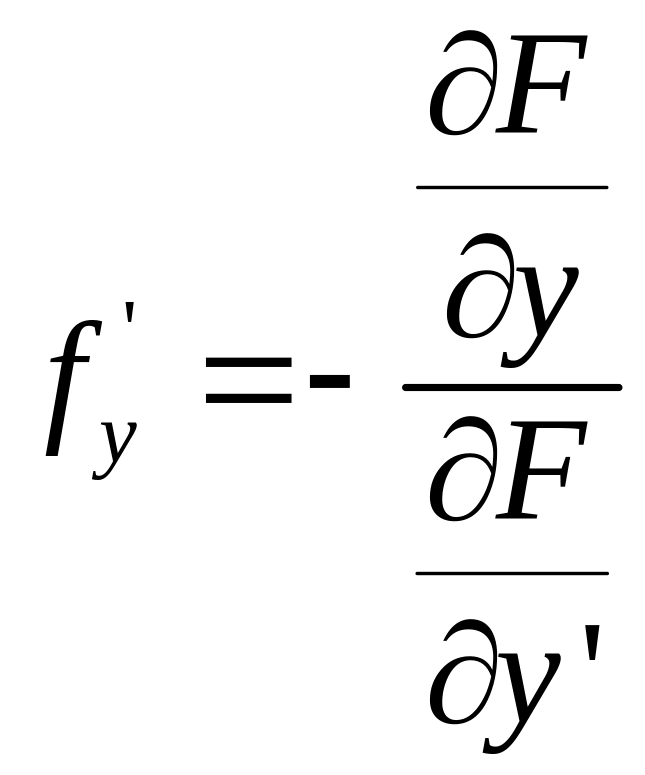
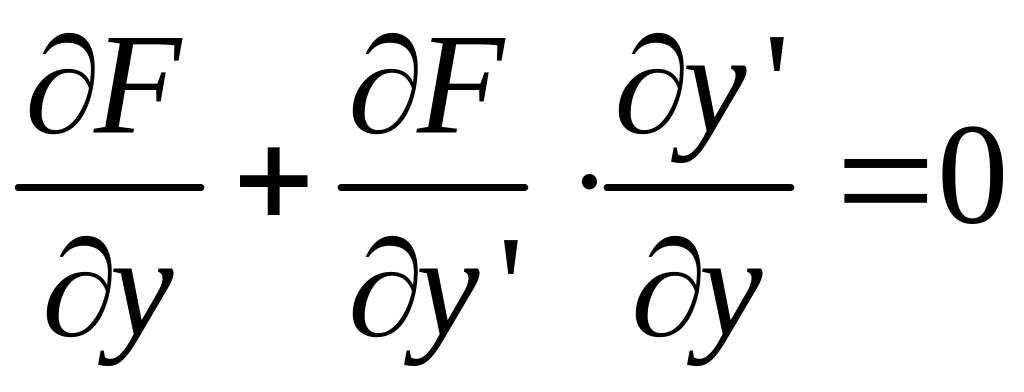
Подозрительными точками на особые решения будут те, где .

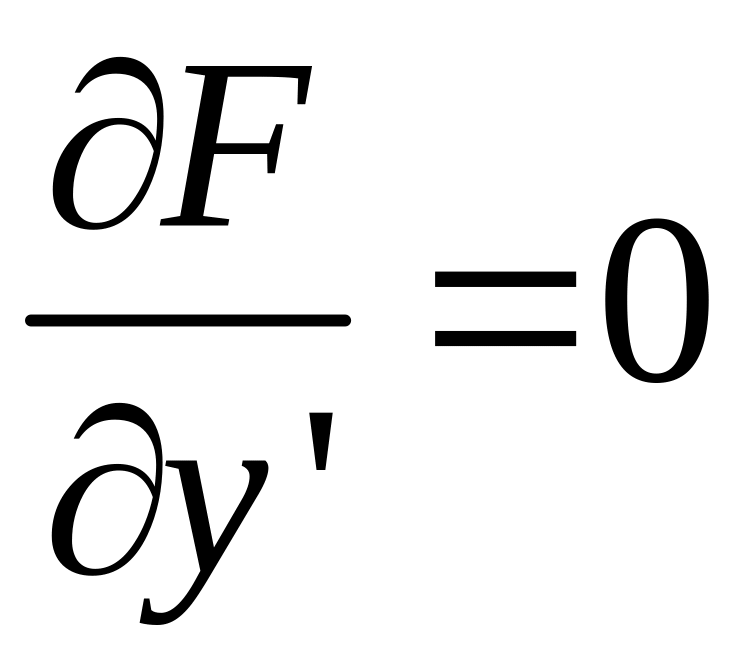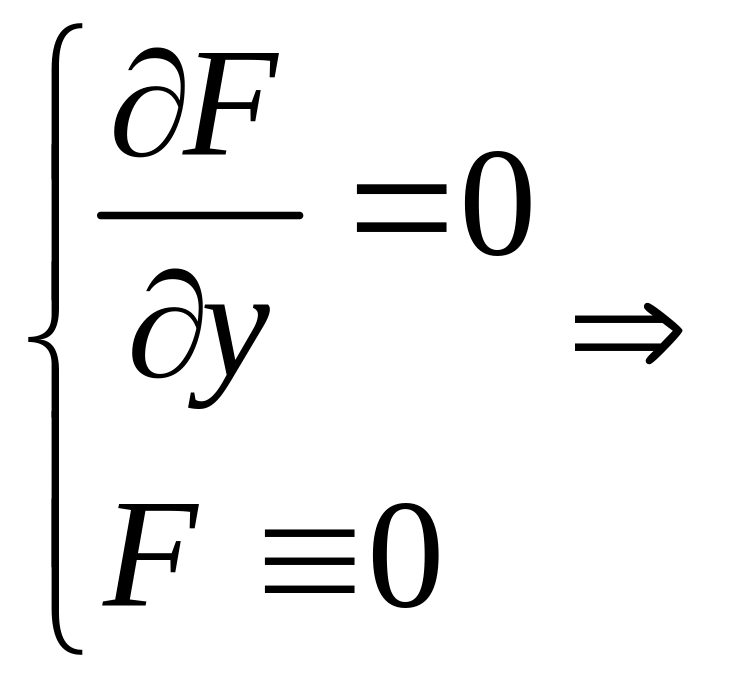особое решение.

Пример

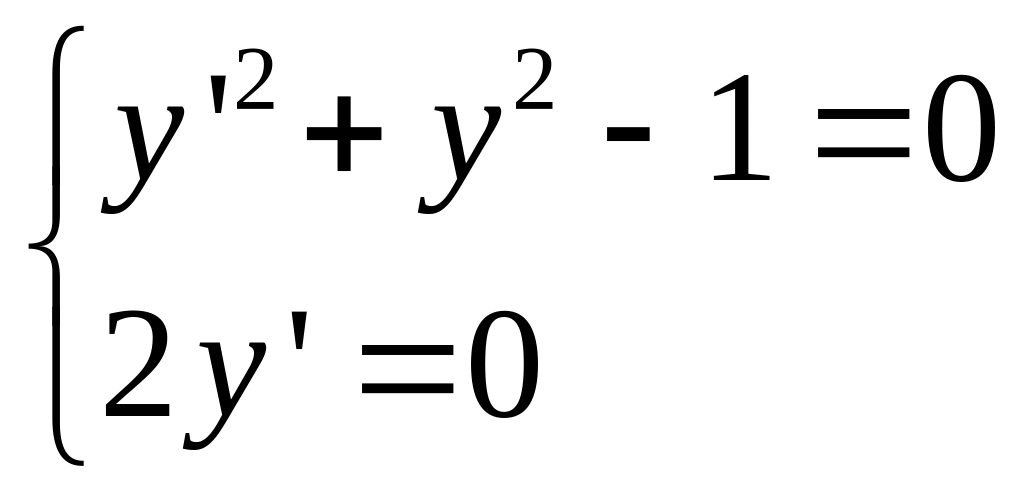
- подозрительные кривые, решение.

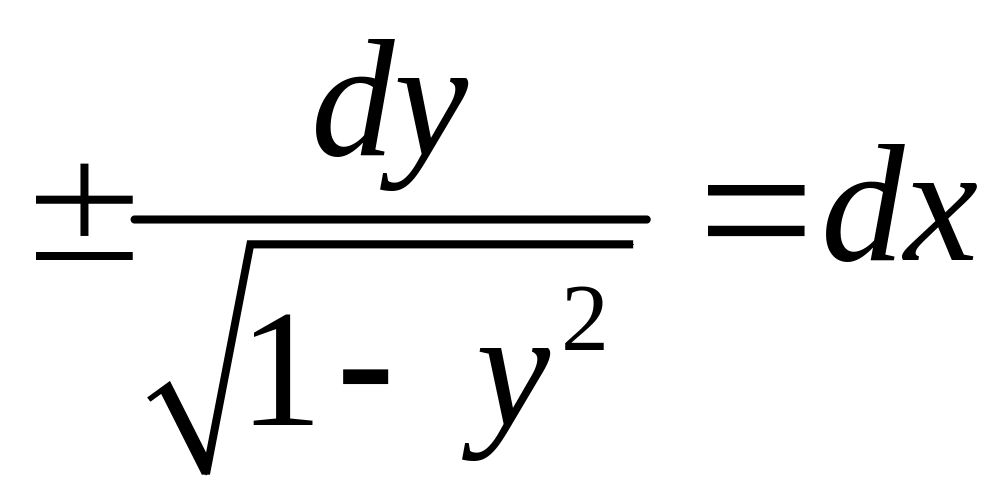
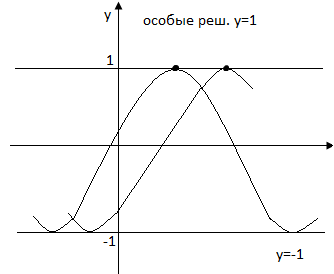
13. Дискрименантная кривая

Методы интегрирования уравнений, не разрешенных относительно производной

1. Метод параметра

Применяется, когда в явном виде выражается у или х.

- уравнение Лагранжа

- уравнение Клеро (частный случай уравнения Лагранжа)

Решение ищем в следующем виде:

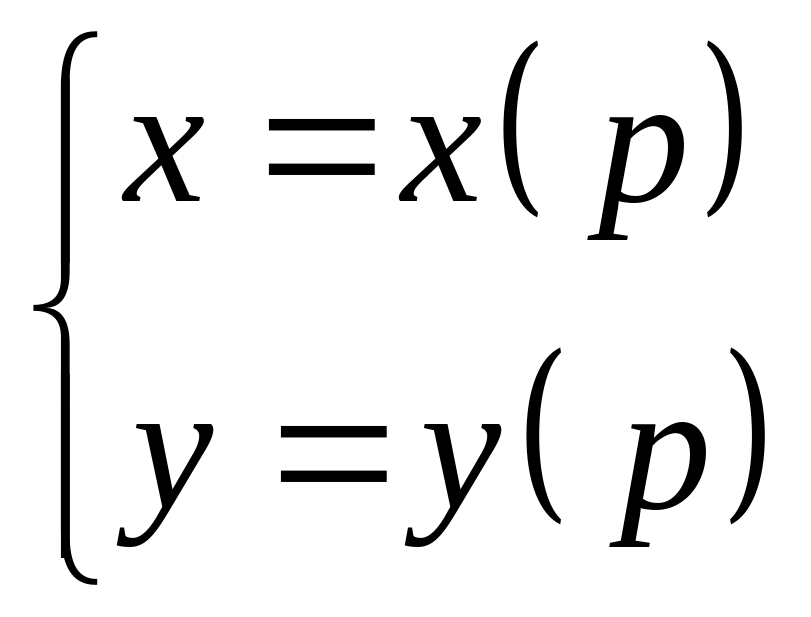, р – параметр

- уравнение окрестности в параметрическом виде.

- неявный вид.

- явный вид.

В качестве возьмем Тогда , надо найти .

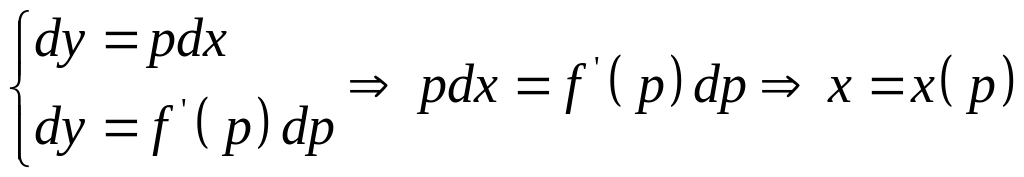
Ответ: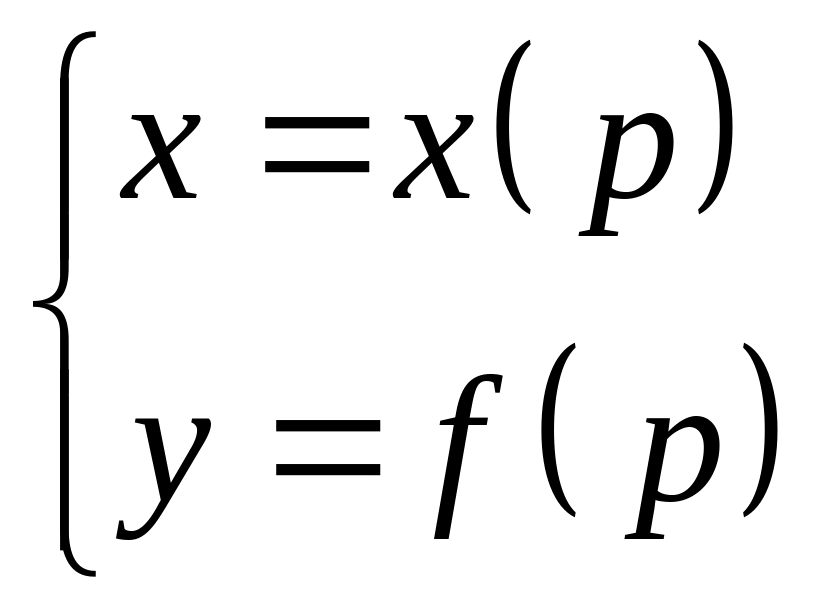

Пример

- ?

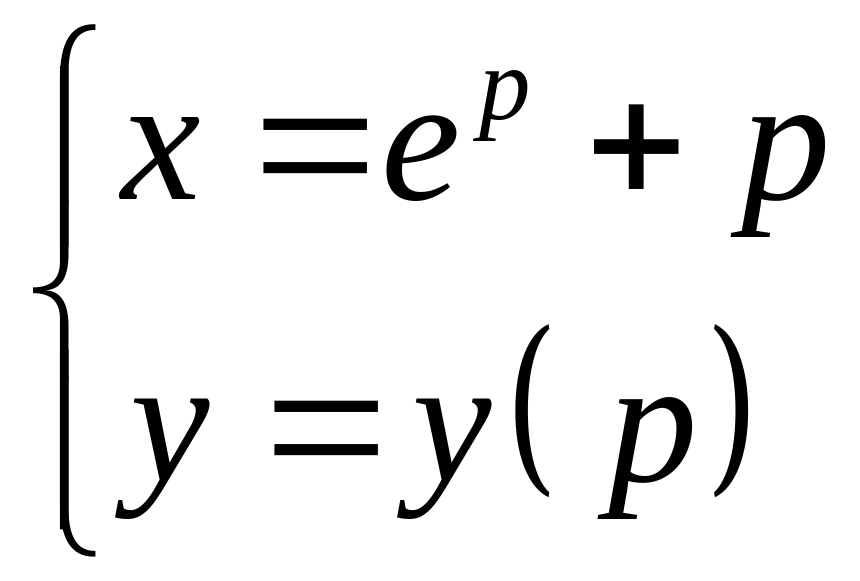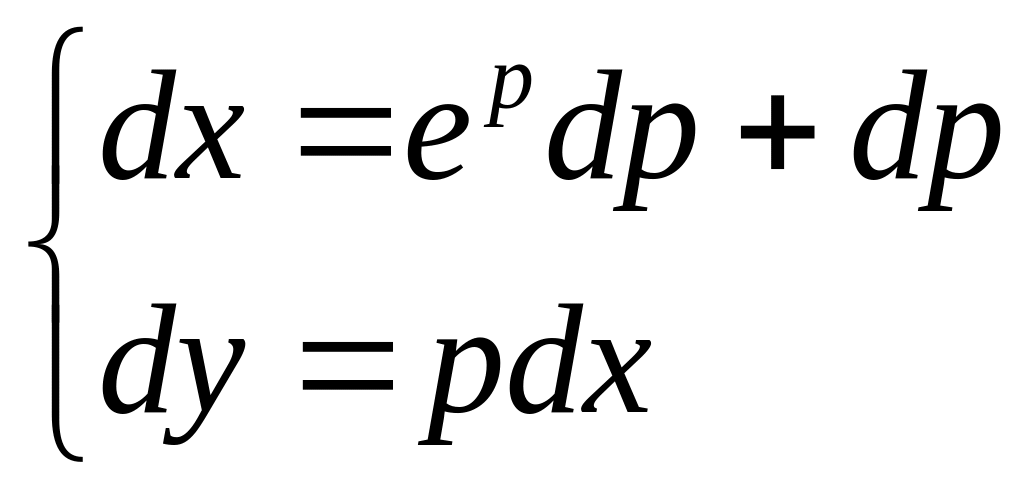
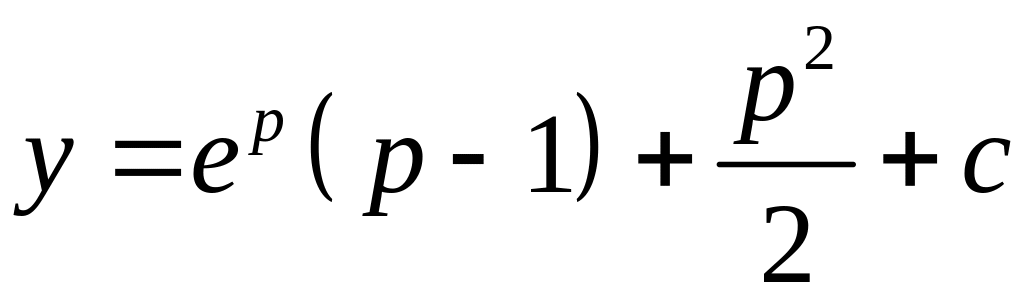
Ответ:

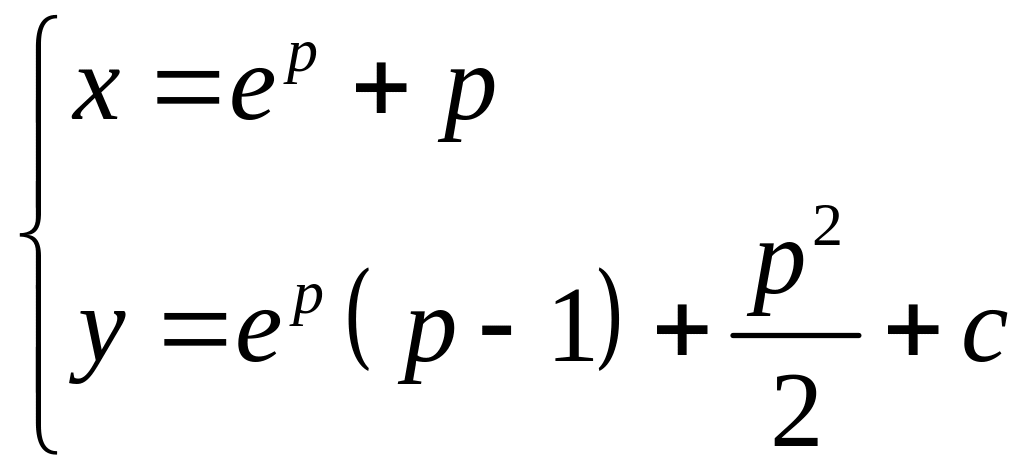
Уравнение Клеро также решается методом параметров.

Пример.

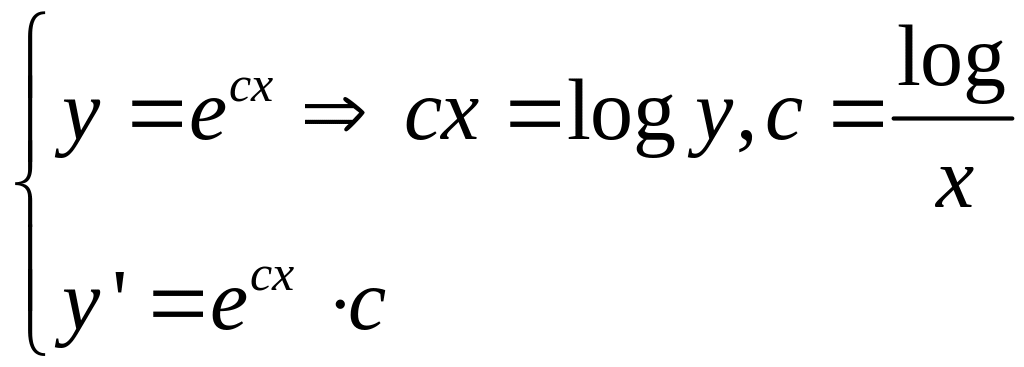
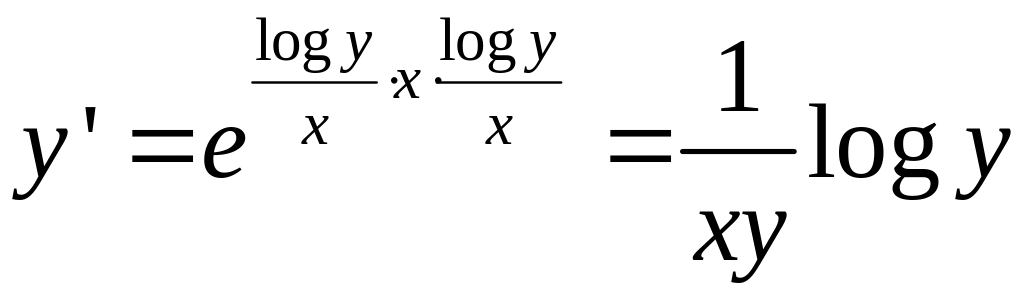
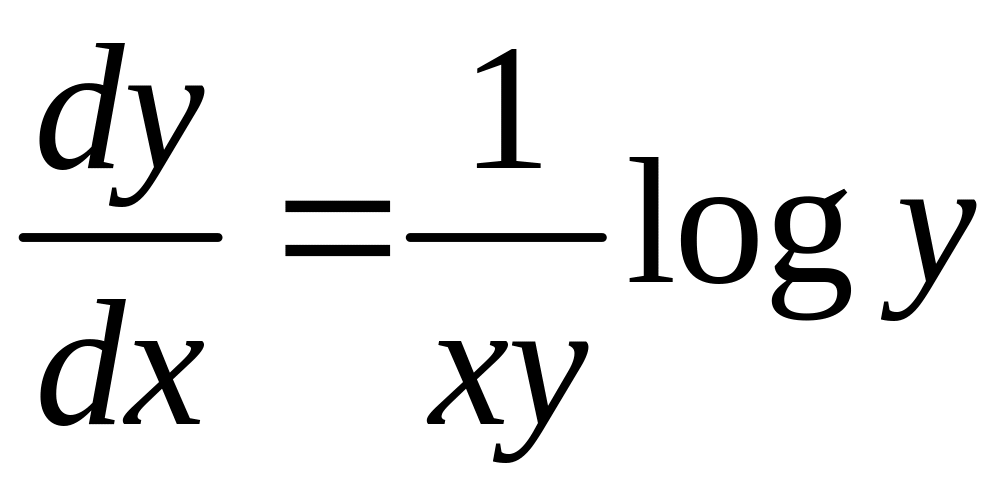
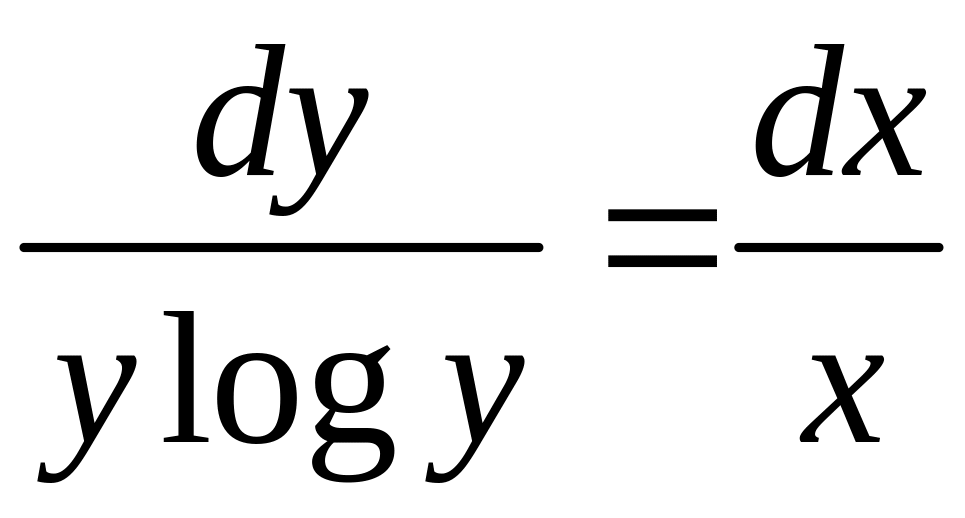
- общее решение.