
- •Содержание
- •1. Введение
- •Определение
- •2. Задача Коши – решение дифференциального уравнения, так что выполняется начальные условия
- •Определение
- •5. Линейные уравнения
- •6. Нахождение частного решения оу Метод Бернулли
- •7. Задачи
- •8. Уравнения в полных дифференциалах
- •Определение
- •14. Огибающее семейство кривых Определение
- •Теорема
- •Теорема
- •19. Решение неоднородных уравнений
- •Метод неопределенных коэффициентов
- •20. Метод неопределенных коэффициентов
- •21. Определитель системы - определитель Вронского
- •22. Линейные уравнения с переменными коэффициентами
- •23. Дискретные задачи. Задачи с дискретным временем. (Рекуррентные последовательности)
- •24. Гармонические колебания
- •25. Система линейных уравнений с постоянными коэффициентами
- •26. Сведение системы из n-уравнений к одному уравнению n-го порядка
- •27. Решение систем общего вида
- •28. Решение неоднородных систем
- •Метод неопределенных коэффициентов
- •Теорема о существовании единственности (тсе)
14. Огибающее семейство кривых Определение
Если
![]() - уравнение семейства кривых, то кривая
- уравнение семейства кривых, то кривая
![]() - называется огибающей для семейства
кривых, если каждая кривая
каксается другой кривой из семейства.
- называется огибающей для семейства
кривых, если каждая кривая
каксается другой кривой из семейства.
Как найти огибающие?
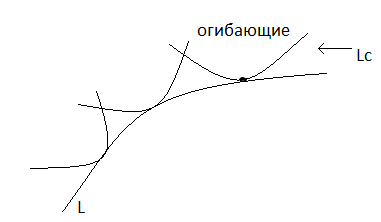
![]()
Фиксируем точку
(х,у), через эту точку проходят 2 кривые
![]() и
и
![]() ,
перемещаясь вдоль огибающей получим,
что
,
перемещаясь вдоль огибающей получим,
что
![]() .
.
Получаем тождество:
![]() для точек огибающей.
для точек огибающей.
Продифференцируем по х
![]() 0
0
В этой точке можно
дифференцировать кривую семейства, на
ней
![]()
![]()
Получим систему:
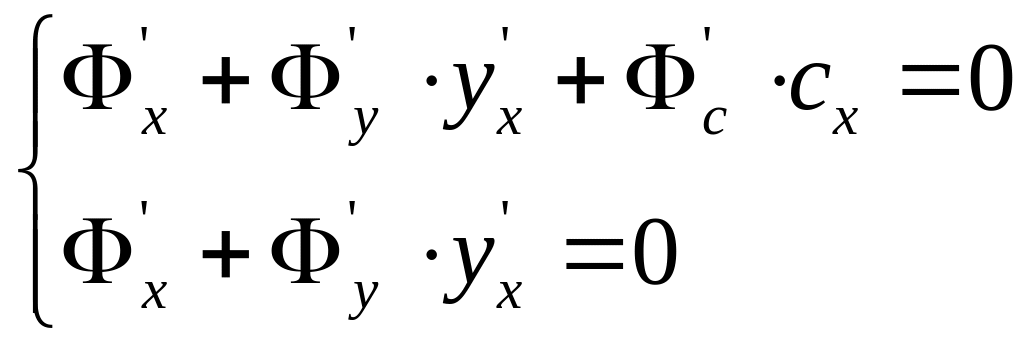
![]()
Итак, для уравнения огибающей надо решить систему.
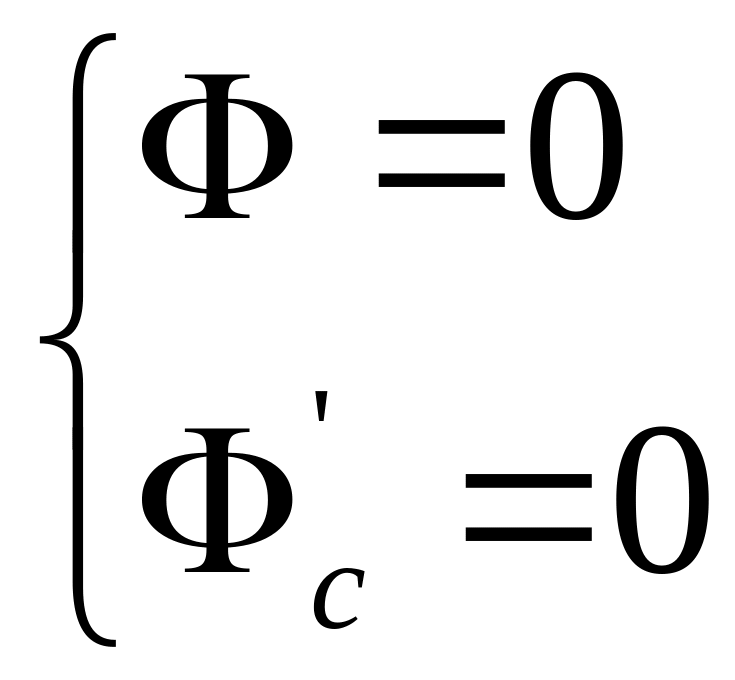
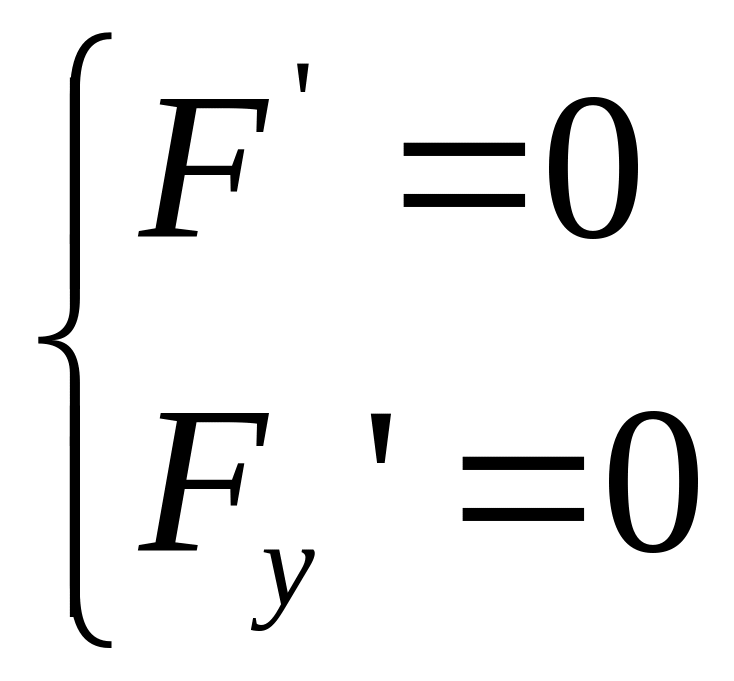
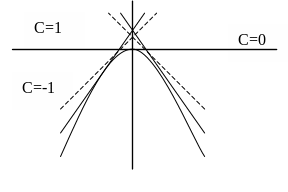
15. Уравнение Клеро
,
где
![]() - известно.
- известно.
Метод параметра:
![]()
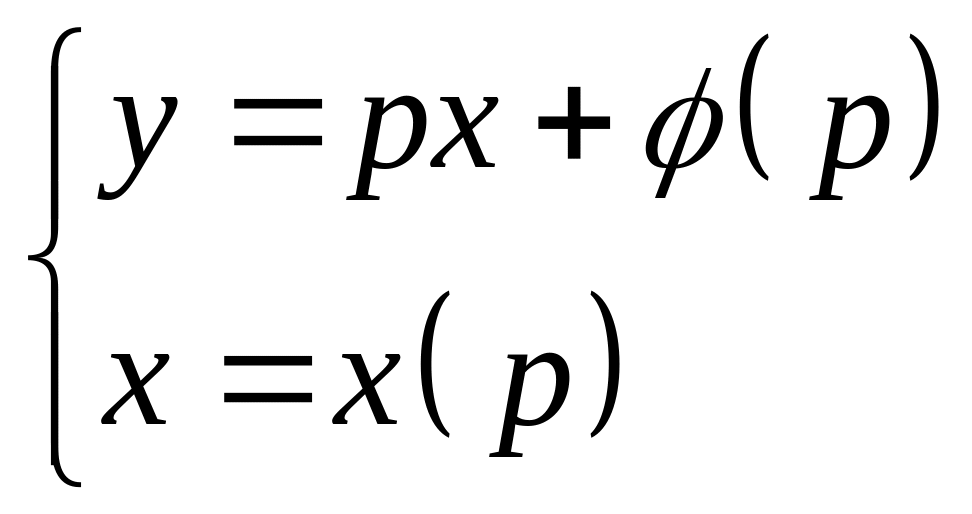

![]()
![]()
![]()
![]() -
общее решение.
-
общее решение.
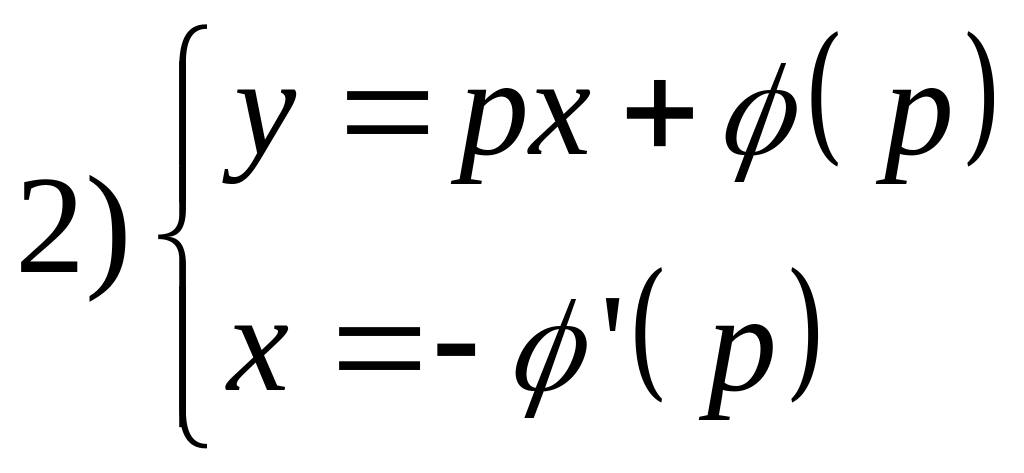 -
еще одно решение (особое)
-
еще одно решение (особое)
|
|
![]()
![]() - общее решение
- общее решение
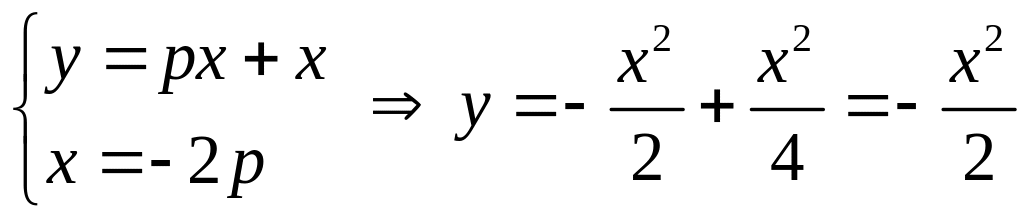
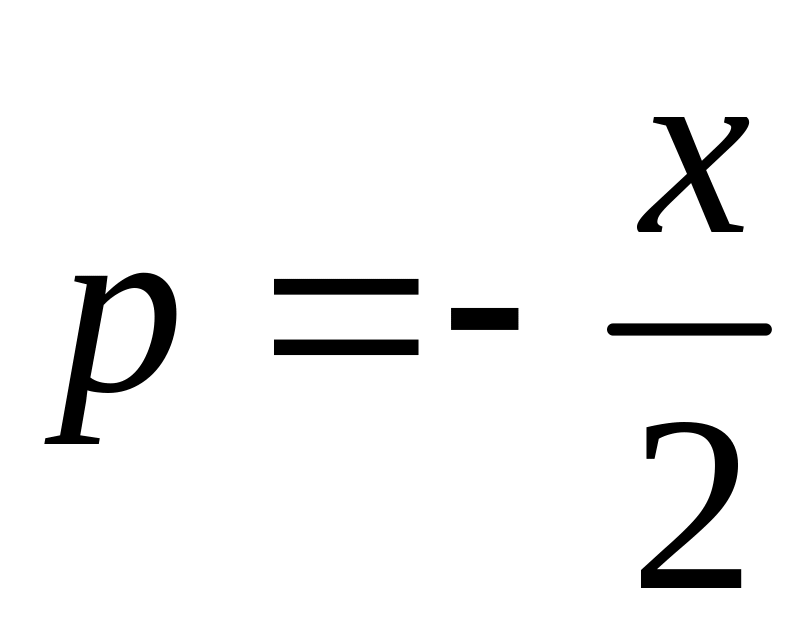
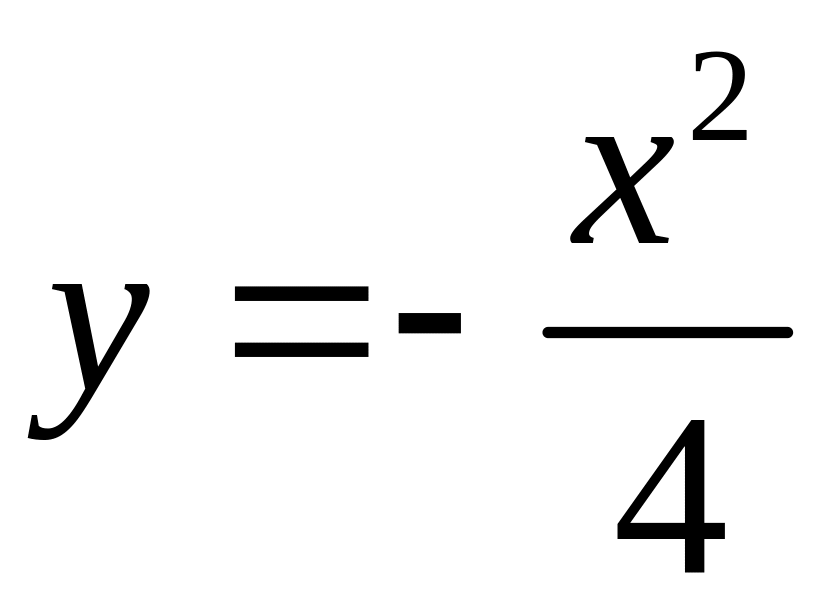
16. Ортогональные траектории
Надо найти семейство кривых которые в каждой своей точке ортогональны соответствующей кривой из
Составим дифференциальное уравнение , для семейства .
В уравнении
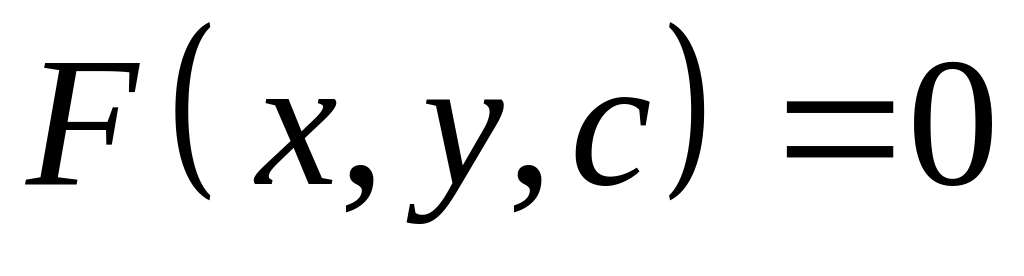 заменяем
заменяем
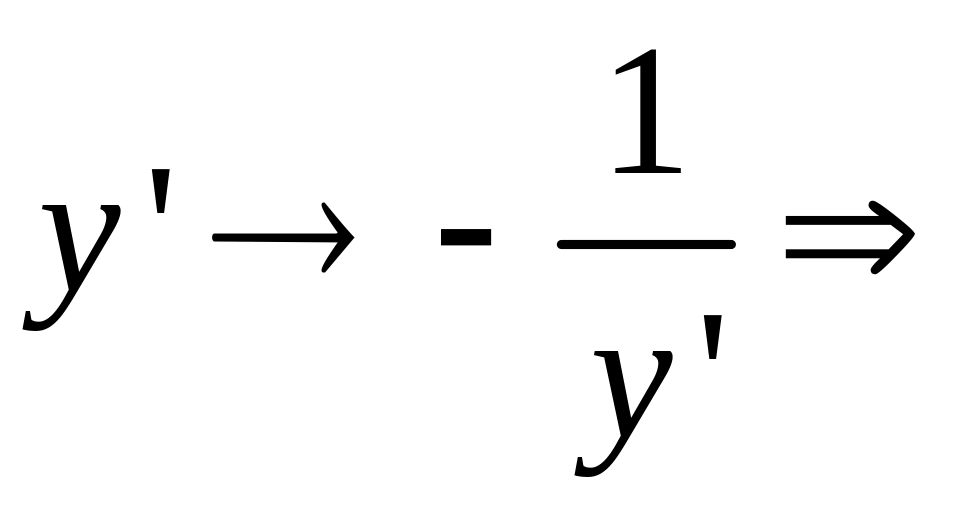 получим
получим
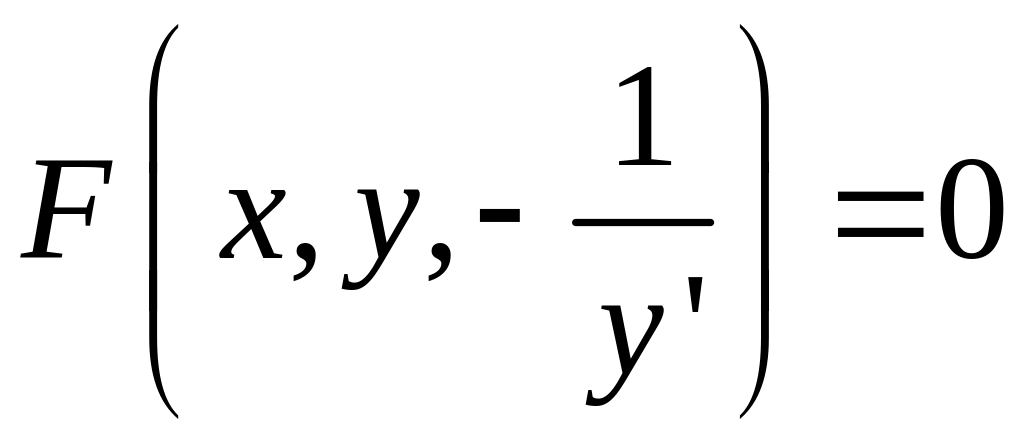 .
Дифференциальное уравнение ортогональных
траекторий.
.
Дифференциальное уравнение ортогональных
траекторий.Общее решение
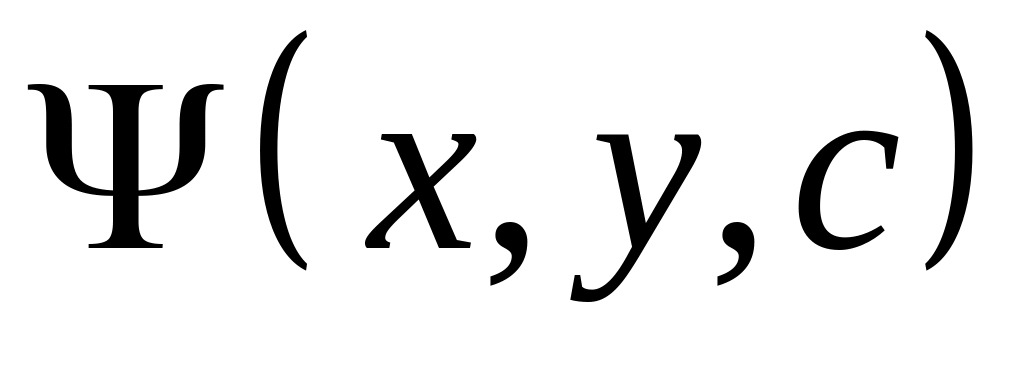 - уравнение ортогональных траекторий.
- уравнение ортогональных траекторий.
Пример
![]()
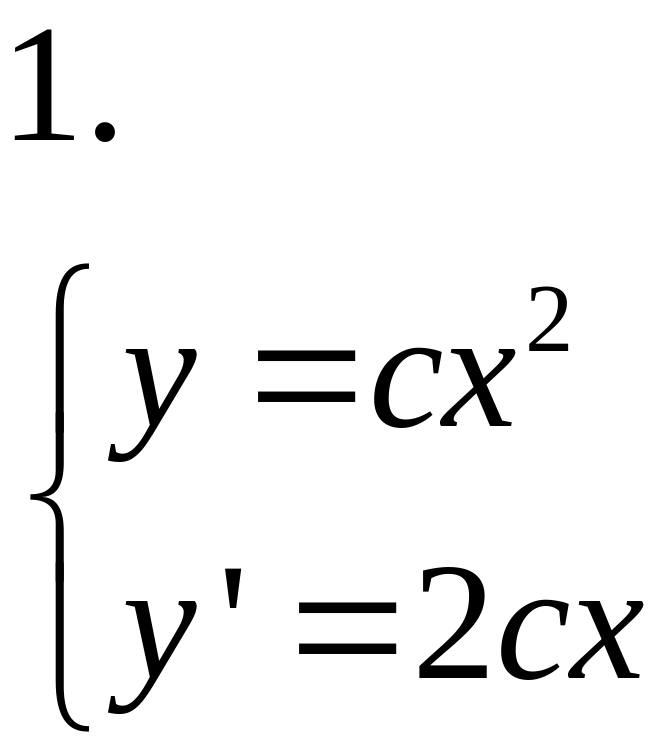
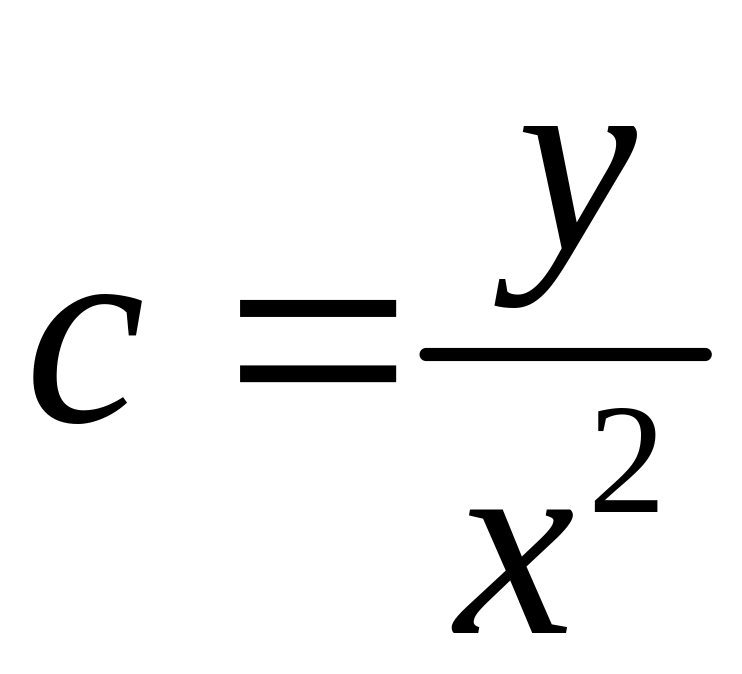
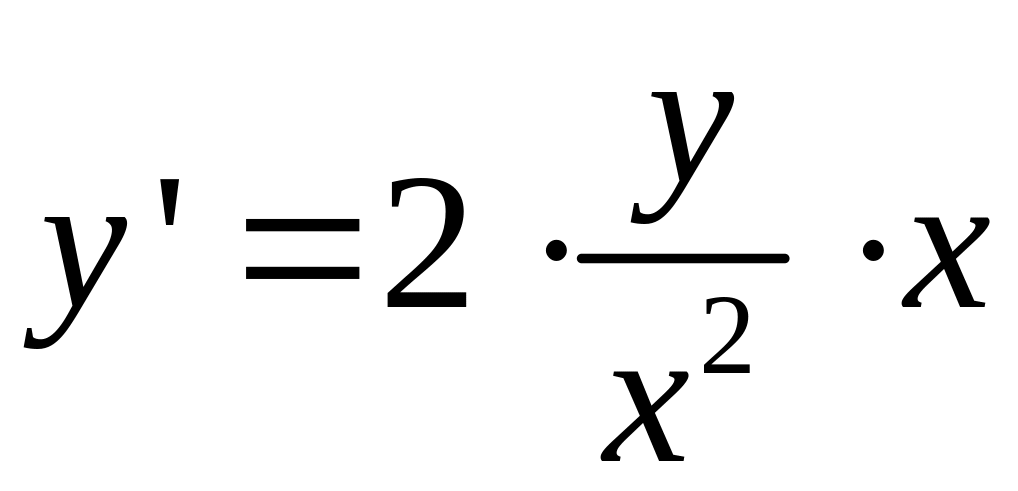
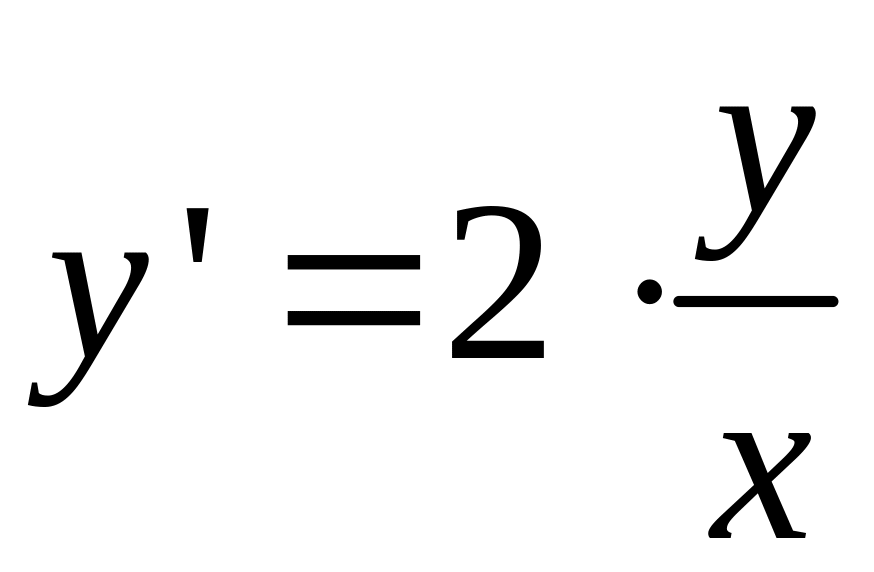
2.
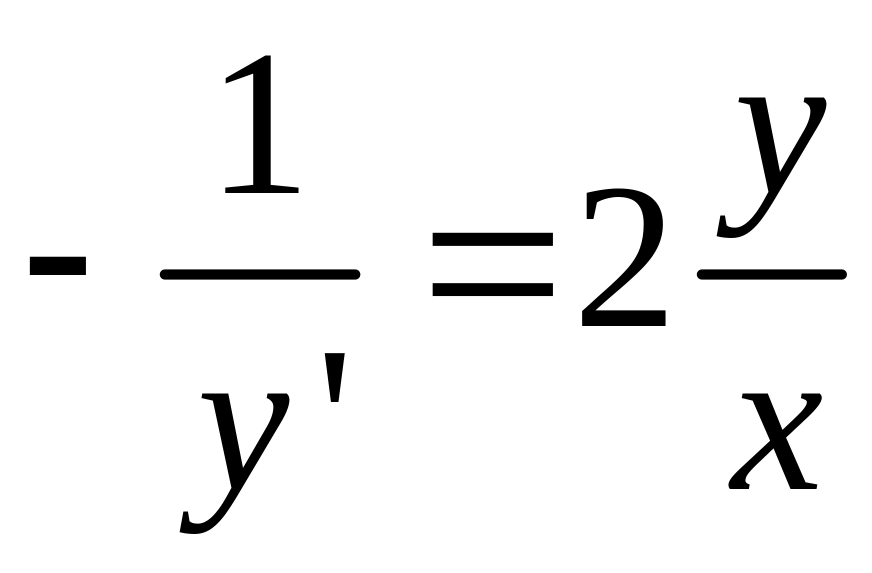
3.

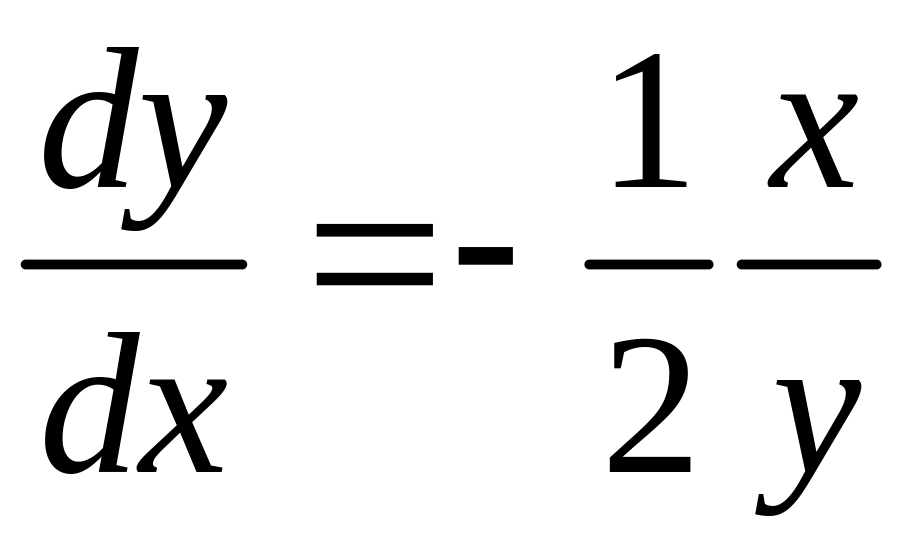
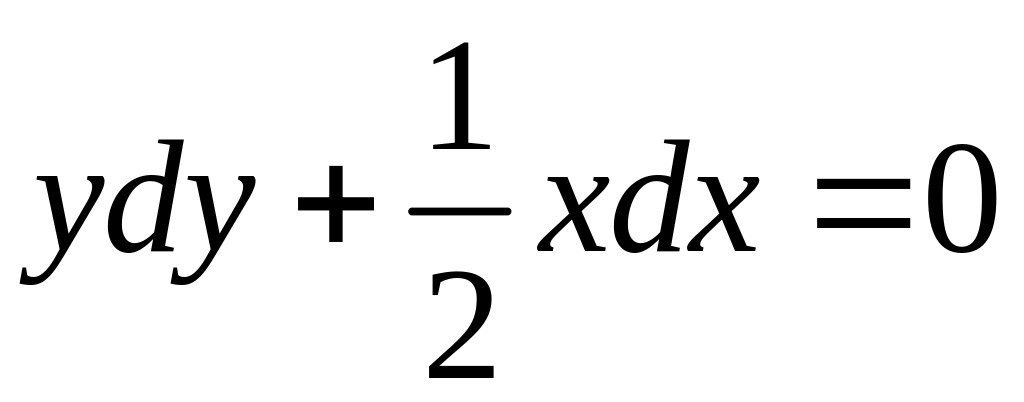
 - ответ
- ответ

17. Уравнения высших порядков
1)
![]() ;
надо n-раз
проинтегрировать
;
надо n-раз
проинтегрировать
2) надо пытаться получить порядок интегрирования
![]()
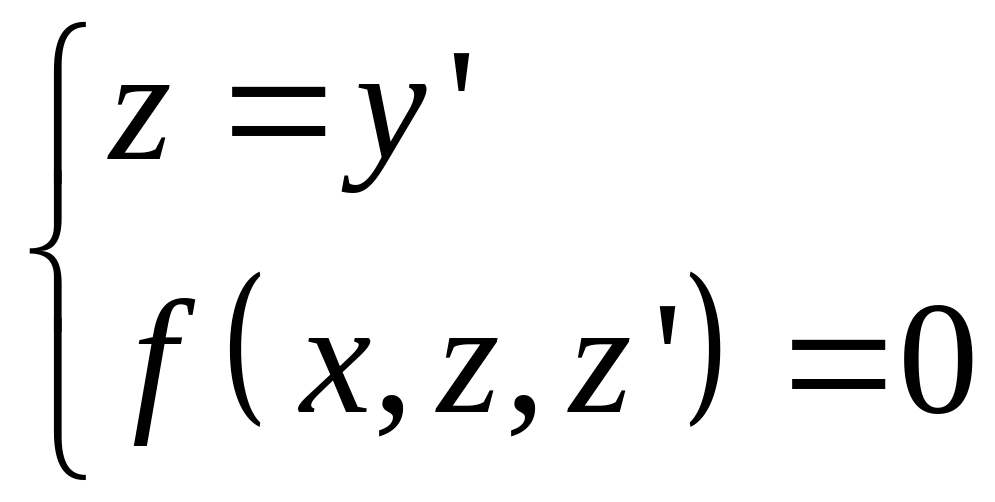
Из 1-го уравнения 2-го порядка, получаем 2 уравнение 1-го порядка
3)![]() (явно отсутствует «x»)
(явно отсутствует «x»)
Введем новую
функцию
![]()
Новая переменная
![]()
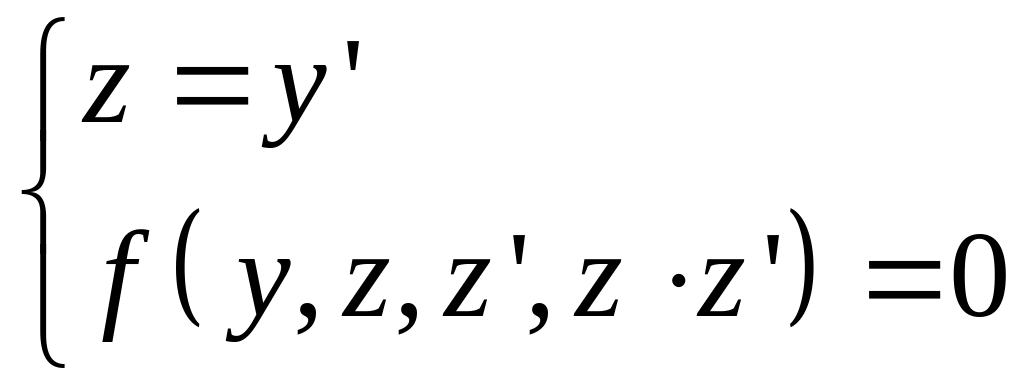
18. Линейные уравнения n-го порядка
![]() (ЛНУ)
(ЛНУ)
![]() функции
от
функции
от
![]()
![]() (ЛОУ)
(ЛОУ)
Можно определить линейный дифференциальный линейный оператор
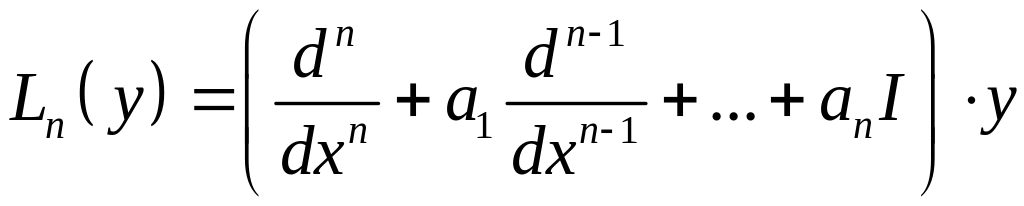
1)Если решаем однородное уравнение
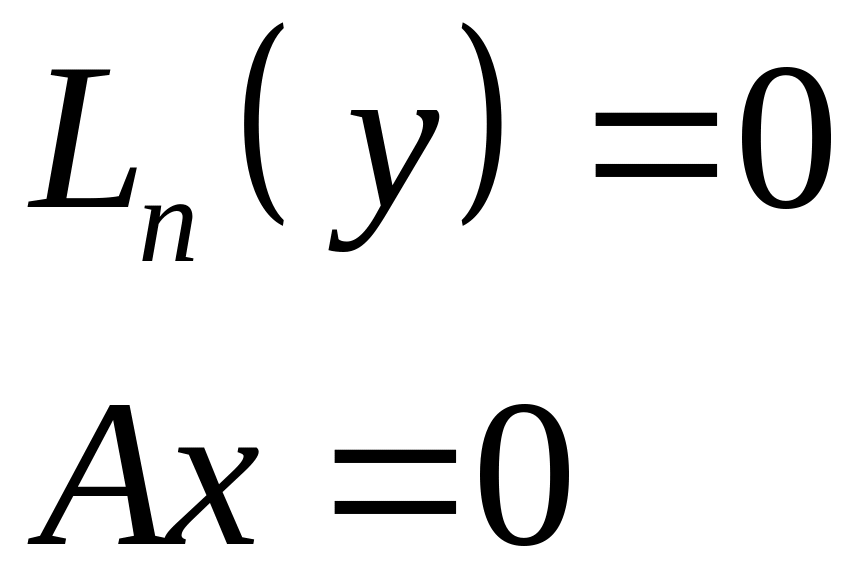
То есть ищем ядро
оператора
![]()
1)![]() - линейное пространство
- линейное пространство
2)![]() - размерность
- размерность
По ТСЕ решение
уравнения
![]() зависит от n
произвольных постоянных
зависит от n
произвольных постоянных
![]()
Пусть
![]() базис
базис

Базис называется фундаментальной системой решений (ФСР).
Если решаем неоднородное уравнение
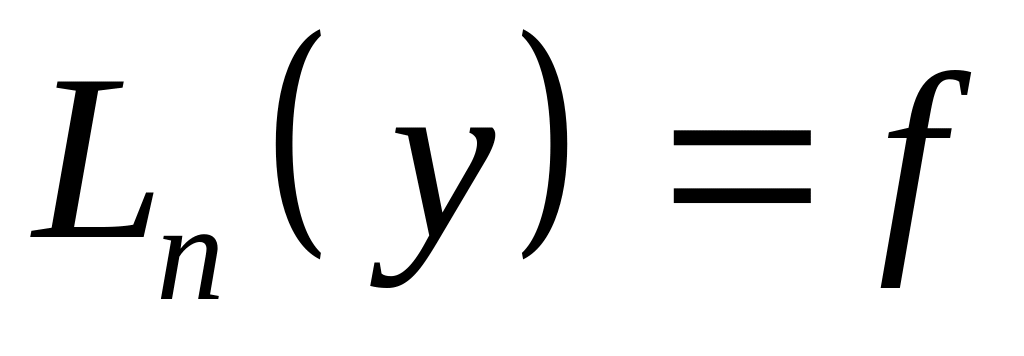 ;
;
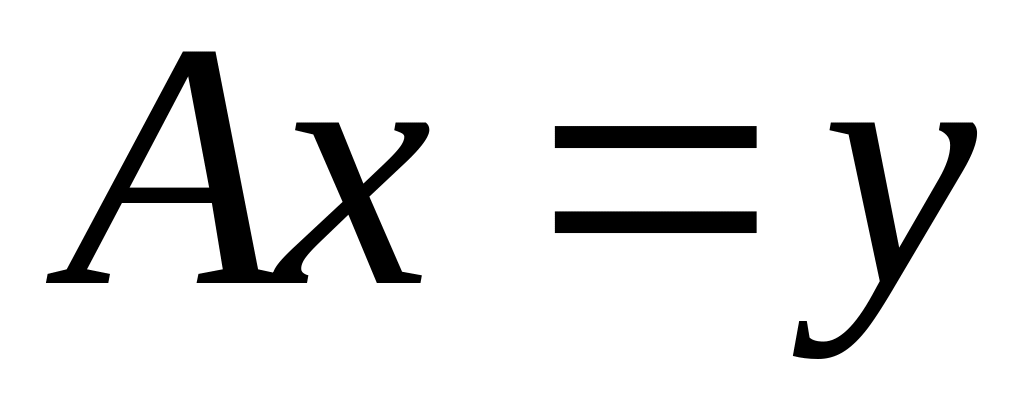
Мы должны уметь
обращать оператор
![]()
Надо подобрать какое-нибудь (частное решение)
Пусть это будет , тогда общее решение этого же уравнения
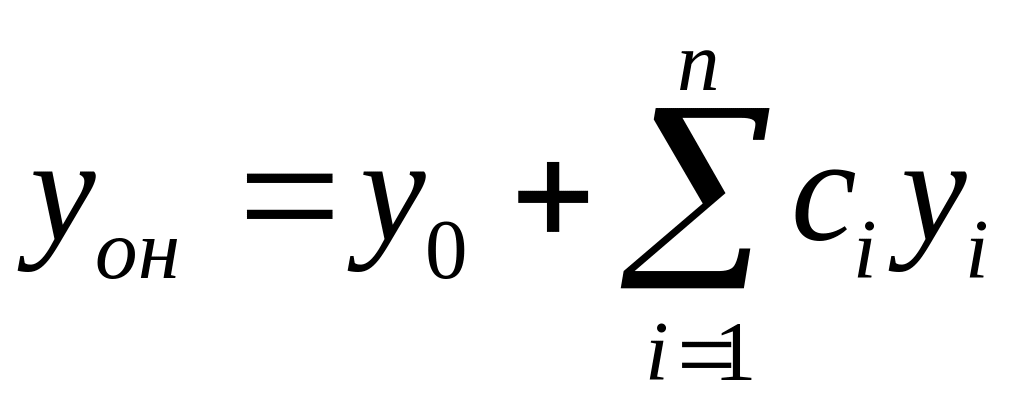 - структура общего
решения ЛНУ
- структура общего
решения ЛНУ
Линейное уравнение с постоянными коэффициентами
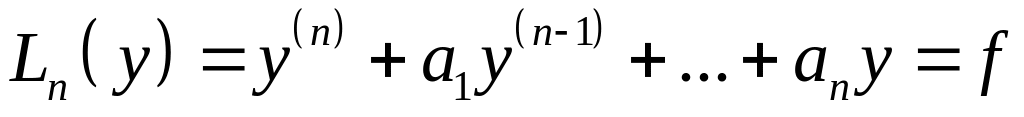
![]()
С каждым дифференциальным оператором связок характеристический полином.
![]()
где
![]() - корни.
- корни.
Аналогично разложим дифференциальный оператор на множители
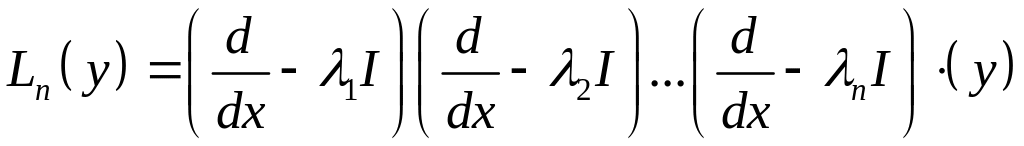
Пример

![]()
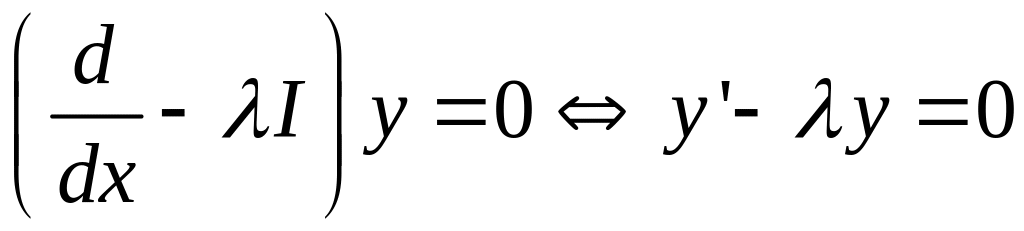
![]() - решение
- решение
![]() - общее решение
- общее решение
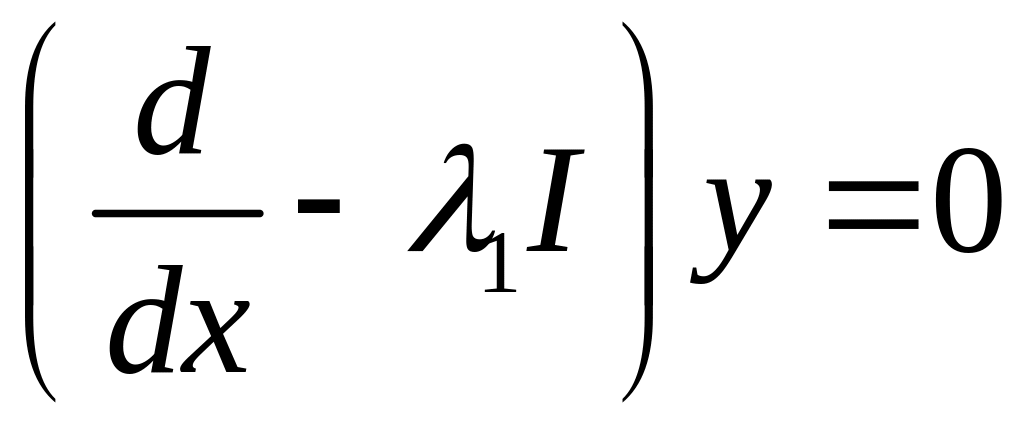
Вывод: если
![]() - корни характеристического полинома,
то
- корни характеристического полинома,
то
![]() - решения ЛОУ
- решения ЛОУ
а) предположим,
что все корни различны, тогда все
![]() - различные функции (если они линейно
независимы, то образуют ФСР)
- различные функции (если они линейно
независимы, то образуют ФСР)
![]() - общее решение
ЛОУ.
- общее решение
ЛОУ.
Теорема
Пусть
![]() и различны,
- линейно независимы.
и различны,
- линейно независимы.
Доказательство:
От противного,
![]() (не все равные нулю)
(не все равные нулю)
![]()
![]()
![]()
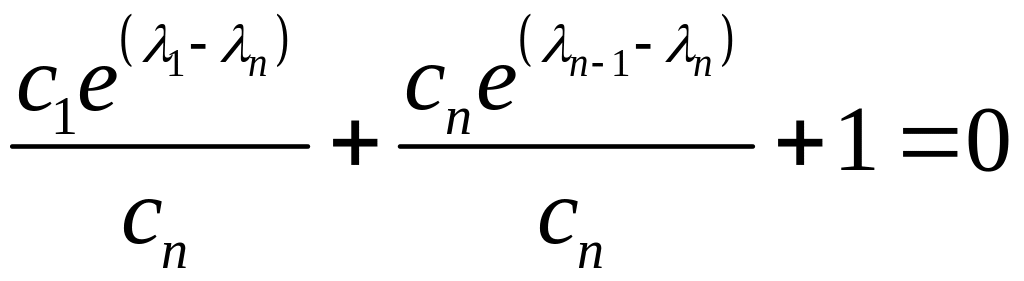
![]()
Пример
![]()
![]()
![]()
![]()
![]()
4)Кратные корни
![]()
![]() - решение, но
некоторые из них совпадают и не могут
быть линейно зависимыми.
- решение, но
некоторые из них совпадают и не могут
быть линейно зависимыми.
![]() не все решения.
не все решения.
Пусть
![]() - корень кратности
- корень кратности
![]()
![]()
![]()
![]()
![]()
Пример
![]()
![]()
![]()
![]()
Теорема
Если
- корень кратности
![]() ,
решением уравнения
,
является функция
,
решением уравнения
,
является функция
![]()
Доказательство:
По индукции, что
верно при
![]() докажем, что верно при
докажем, что верно при
![]() .
.
Пусть - корень кратности
![]()
аналогично для дифференциального оператора.
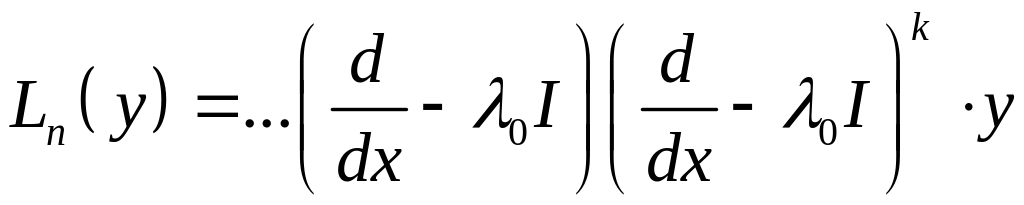
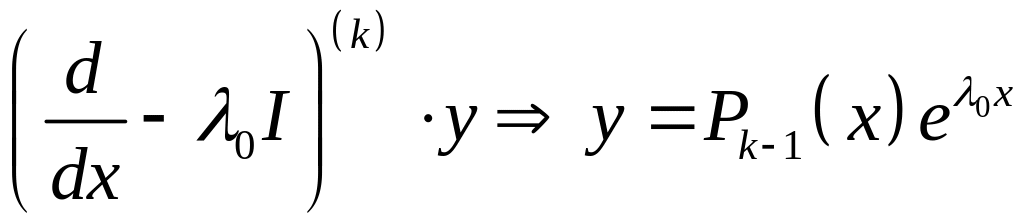
по предложению индукции
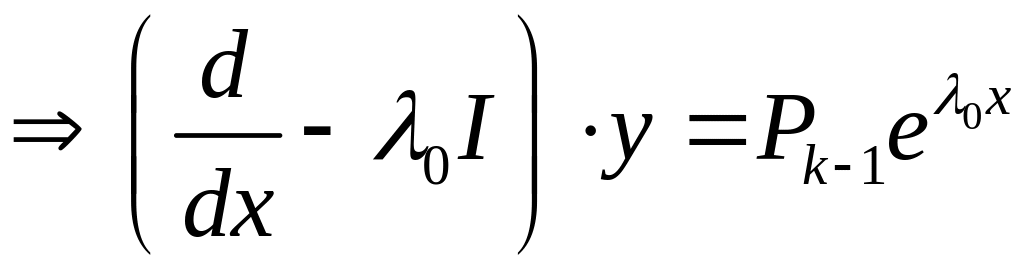
![]() - линейное уравнение
первого порядка.
- линейное уравнение
первого порядка.
Решение этого
уравнения имеет вид:
![]()
Комплексные корни.
Если
![]() комплексный
корень
комплексный
корень
![]()
если уравнение
![]() с вещественными коэффициентами
с вещественными коэффициентами
![]() тоже с вещественными коэффициентами.
тоже с вещественными коэффициентами.
Комплексные корни
входят парами
![]()
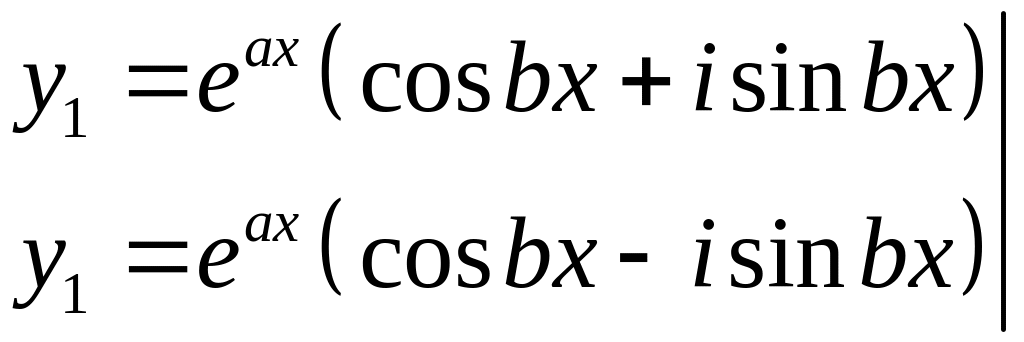
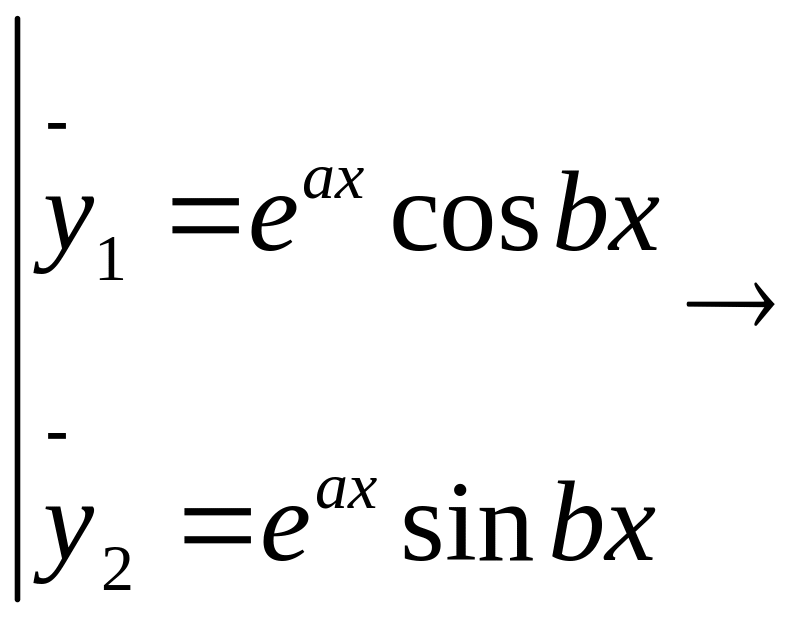 является
решением
является
решением
Вместо этих двух мы возьмем пару линейно независимых функции.
![]()
![]()
Лемма
Если линейный
дифференциал
имеет вещественные коэффициенты и
решение (комплексное) ;![]() - тоже решение.
- тоже решение.
![]()
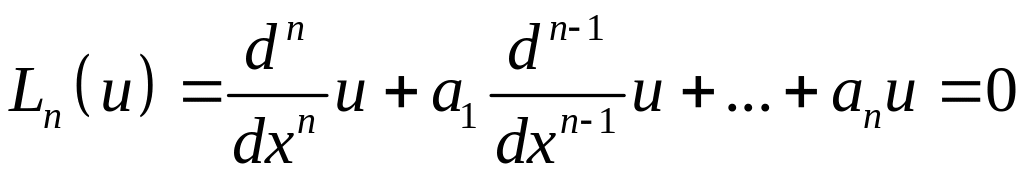
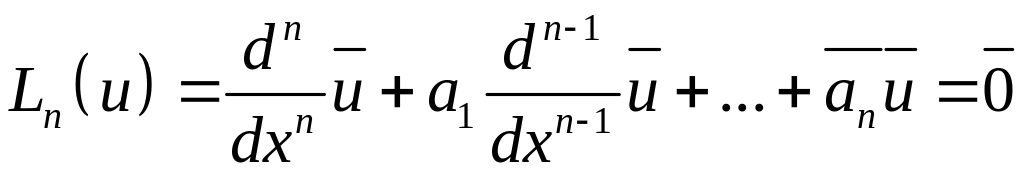
![]()
![]() решение
решение
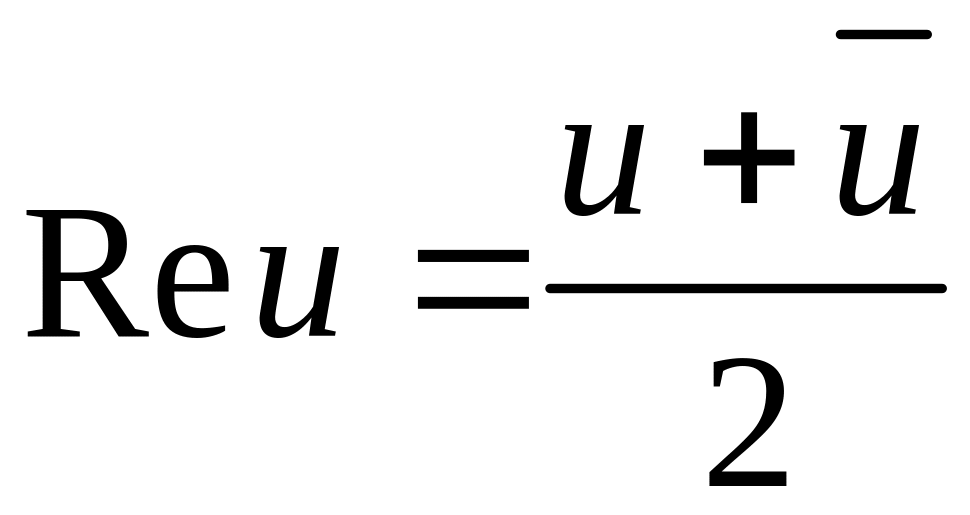
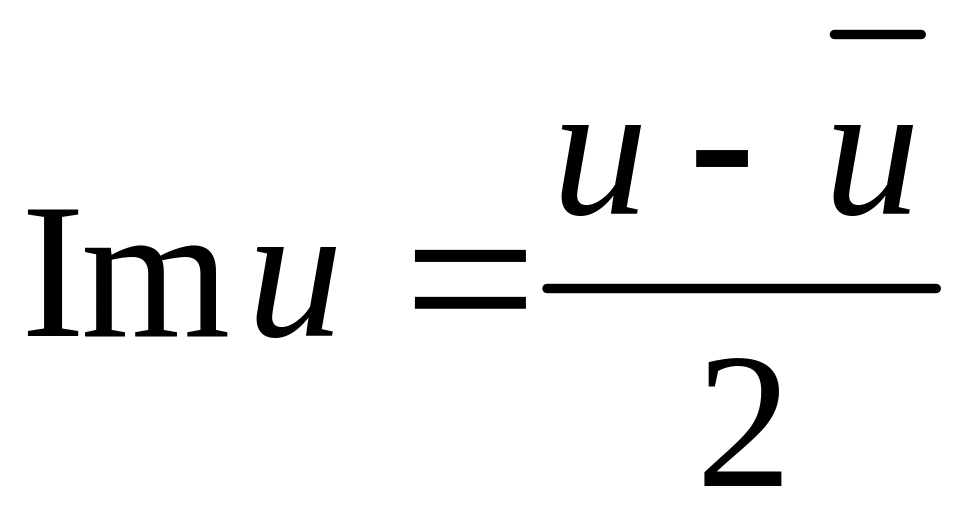
Замечание:
Комплексные кратные
корни, если
![]() имеет корень
имеет корень
![]() кратности
,
кратности
,![]() тоже кратности
тоже кратности
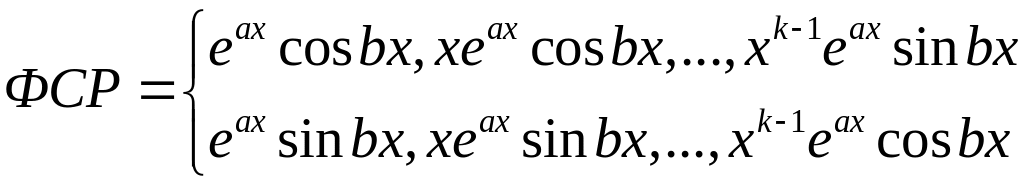
по ним записываем общее решение.
![]()
![]()
![]()
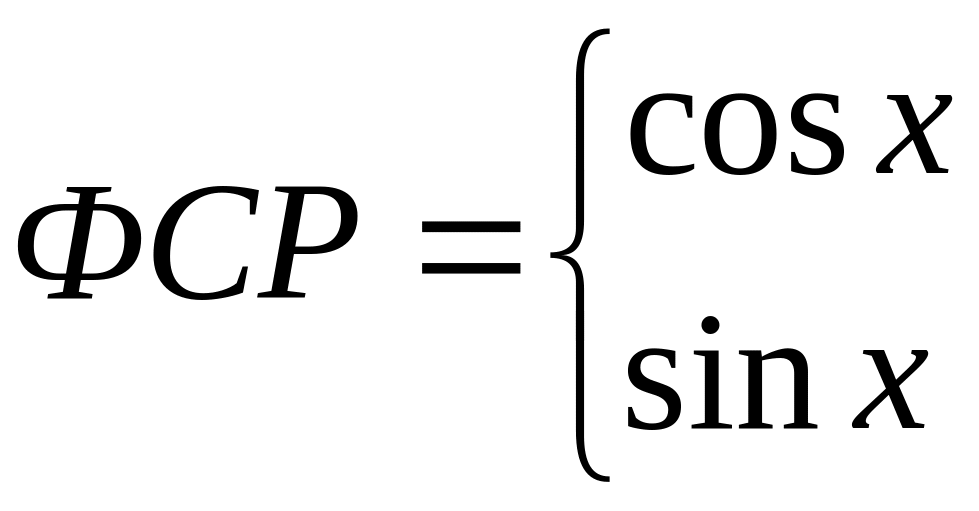
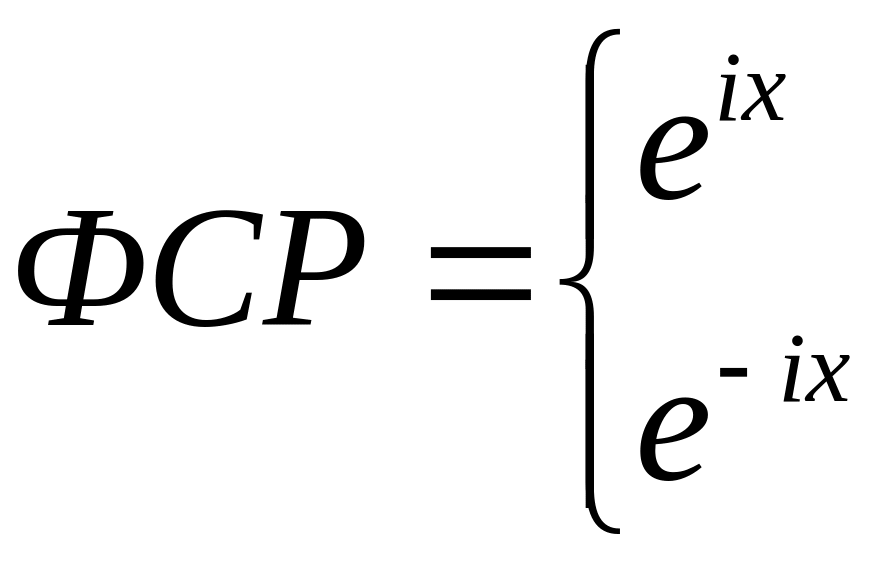
![]()


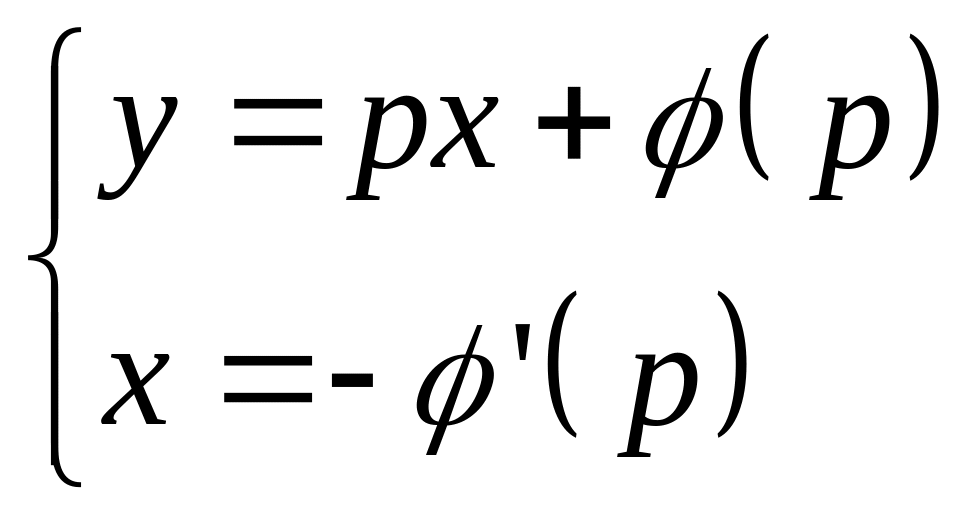 -
особое решение.
-
особое решение.