Содержание
Введение
Задача Коши
Методы решения
Признаки однородности уравнений
Линейные уравнения
Нахождение частного решения ОУ. Метод Бернулли
Задачи
Уравнения в полных дифференциалах
Интегрирующий множитель
Интегрирующие комбинации
Уравнение не разрешенные относительно производной
Особое решение, его поиск (частный случай)
Дискрименантная кривая
Огибающее семейство кривых
Уравнение Клеро
Ортогональные траектории
Уравнения высших порядков
Линейные уравнения n-го порядка
Решение неоднородных уравнений
Метод неопределенных коэффициентов
Определитель системы – определитель Вронского
Линейные уравнения с переменными коэффициентами
Дискретные задачи. Задачи с дискретным временем. (Рекуррентные последовательности)
Гармонические колебания
Система линейных уравнений с постоянными коэффициентами
Сведение системы из n-уравнений к одному уравнению n-го порядка
Решение систем общего вида
Решение неоднородных систем
1. Введение
Обыкновенным дифференциальным уравнениям называется выражение вида:
Где F – функция от (n+2) переменных, x – неизвестная переменная, y – неизвестная переменная которую необходимо найти.
- последовательные производные y.
Пример
Определение
Решением
дифференциальных уравнений, называется
такая функция,
,
которая при подстановке в уравнение
обратит его в верное равенство.
Пример
Решение дифференциального уравнения определяется не однозначно, с точностью до постоянной.
Порядок уравнения определяется по старшей производной, вход в это уравнение:
- второй порядок;
- первый порядок;
Уравнение n-го порядка, зависит от n-произвольных постоянных.
Общим решением дифференциального уравнения, называется выражение вида:
-
произвольные постоянные.
При фиксированных
получаем различные решения.
Перебирая постоянные, получим все решения, бывают исключения, что некоторые решения дифференциального уравнения не записываются в форме общего решения – особые решения.
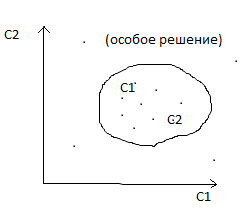
Частное решение, если зафиксированные постоянные в общем решении.
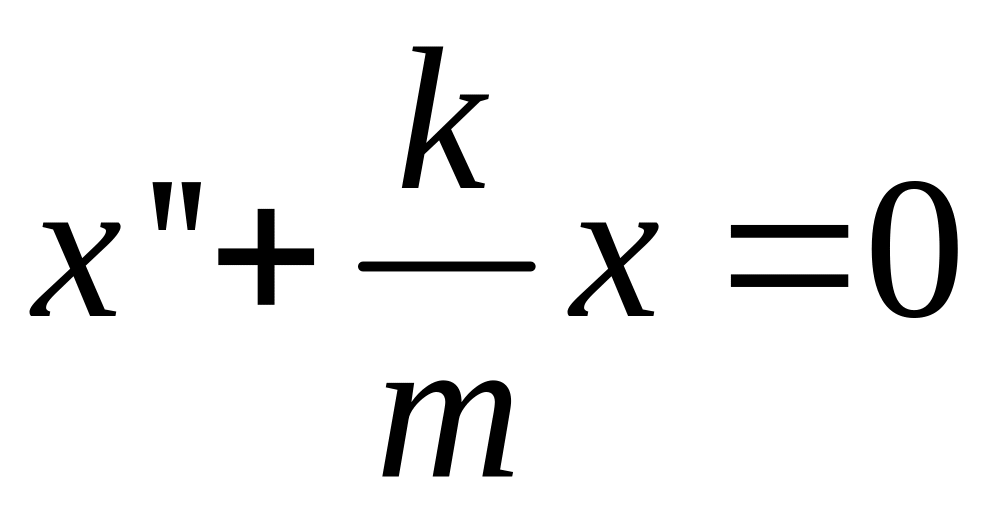
х-координата,
-ускорение.
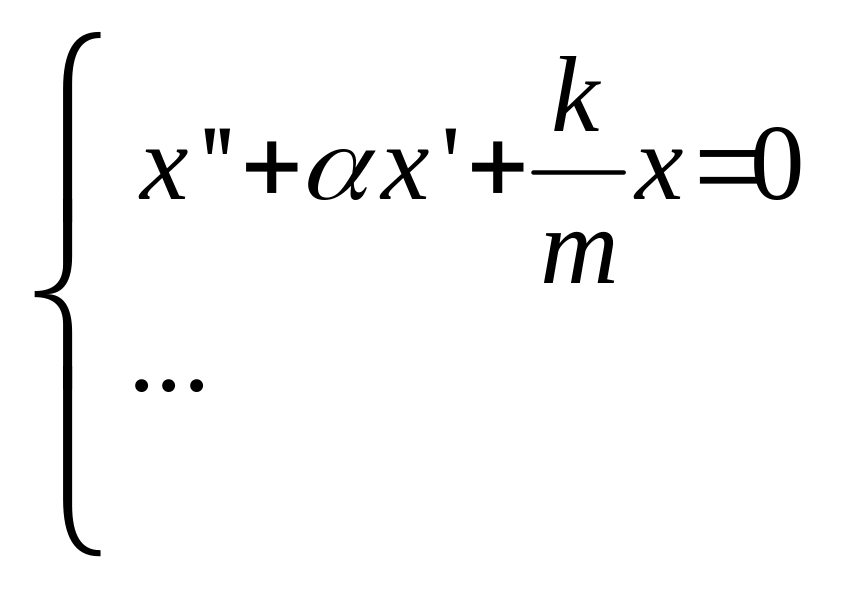
2. Задача Коши – решение дифференциального уравнения, так что выполняется 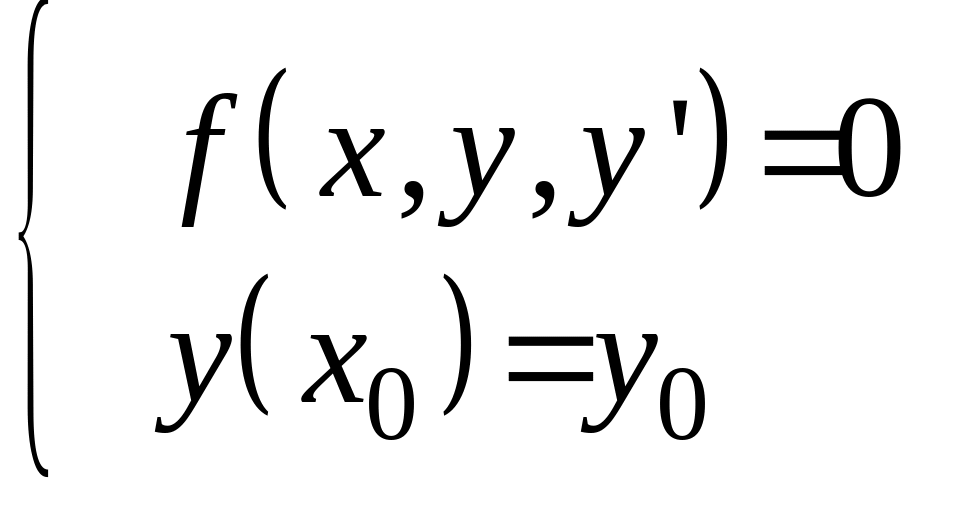начальные условия
-
начальные условия.
Для уравнения n-го порядка ставится n-начальных условий.
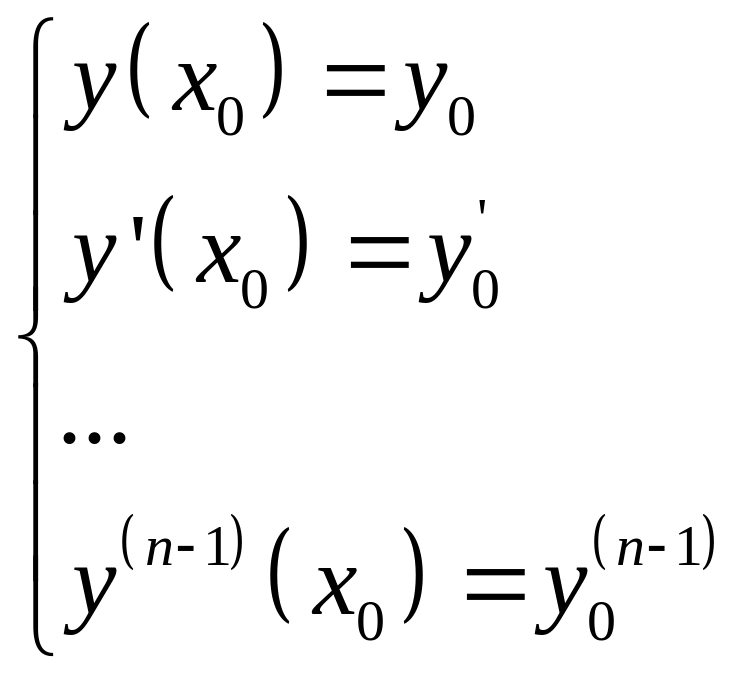
Уравнение 1-го порядка:
- уравнение в
нормальном виде.
Симметричный (дифференциальный) вид.
Геометрическая интерпретация уравнений 1-го рода.
- правая часть
определяет поля направлений.
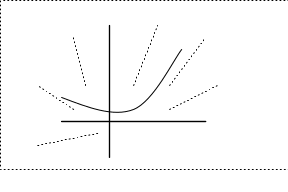
Решение дифференциального уравнения это такая кривая (функция), которая в любой своей точке имеет такой угловой коэффициент касательной, совпадающий с угловым коэффициентом поля направлений в этой точке.
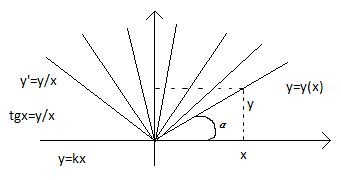
Пример
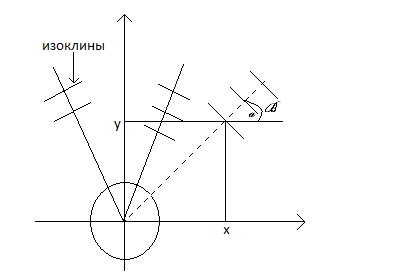
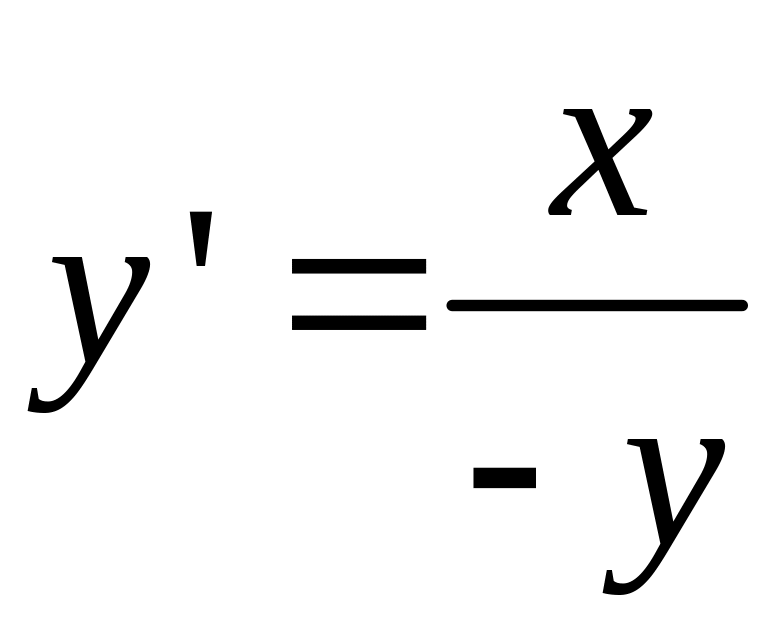
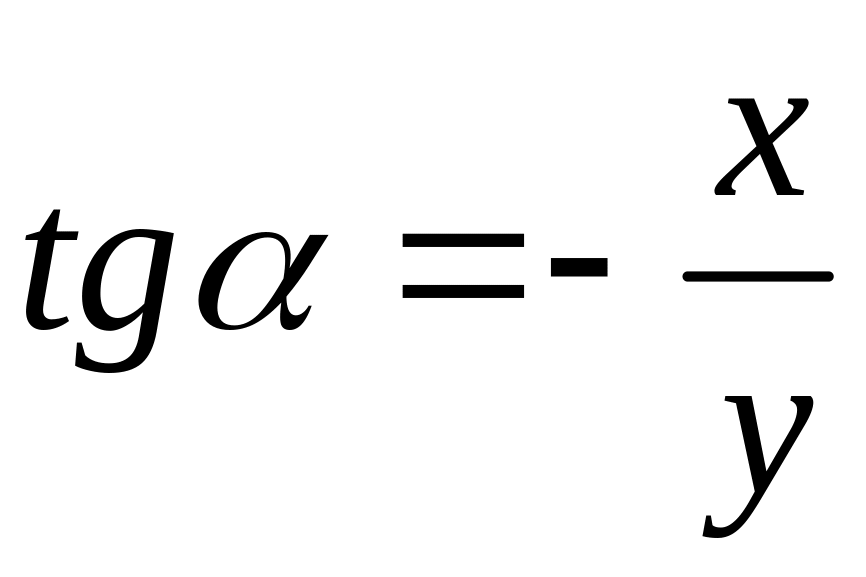
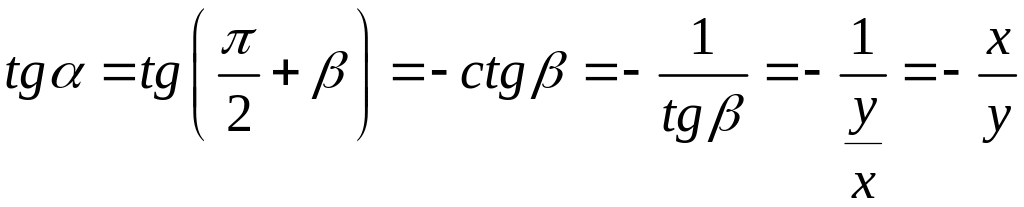
График решений – интегральная кривая.
Теорема (о существовании единственности ТСЕ)
Пусть
непрерывная функция,
– непрерывна в
,
тогда для любой точки
существует единственное решение задачи
Коши:
Изоклины – линии, на которых поля направлений постоянны.
График.
3. Методы решения
Метод разделения переменных
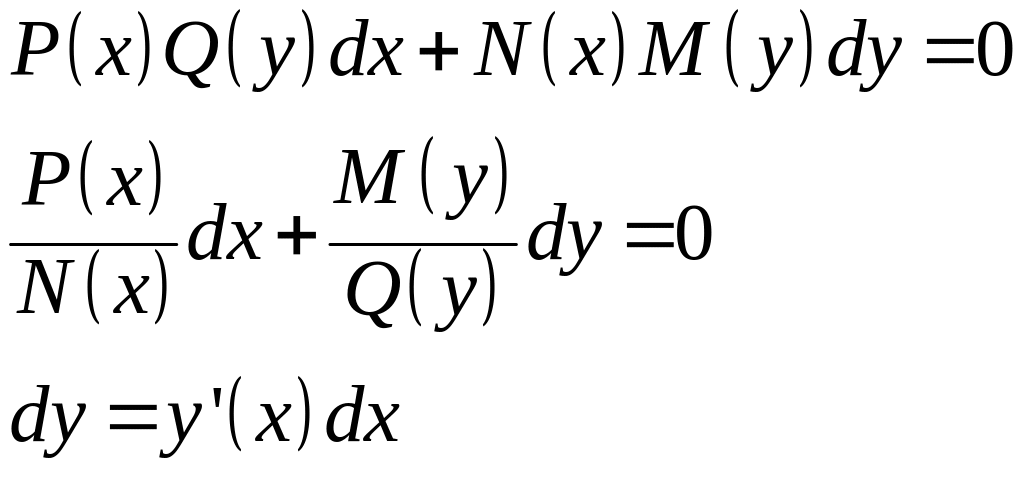
Интегрируем
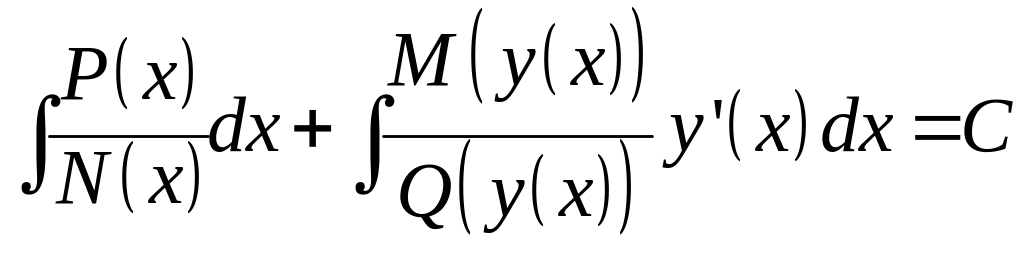
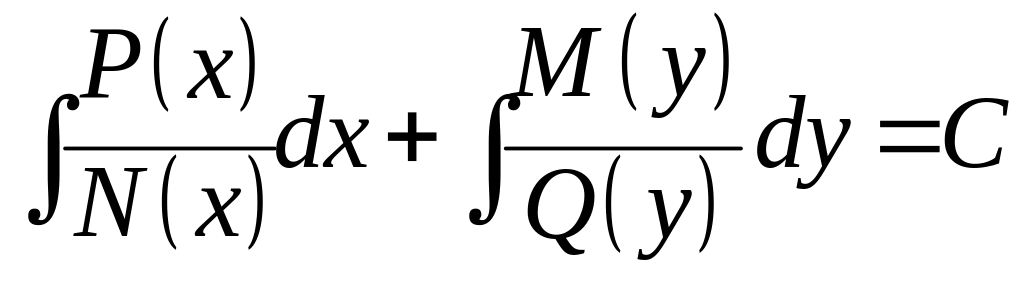
Пример
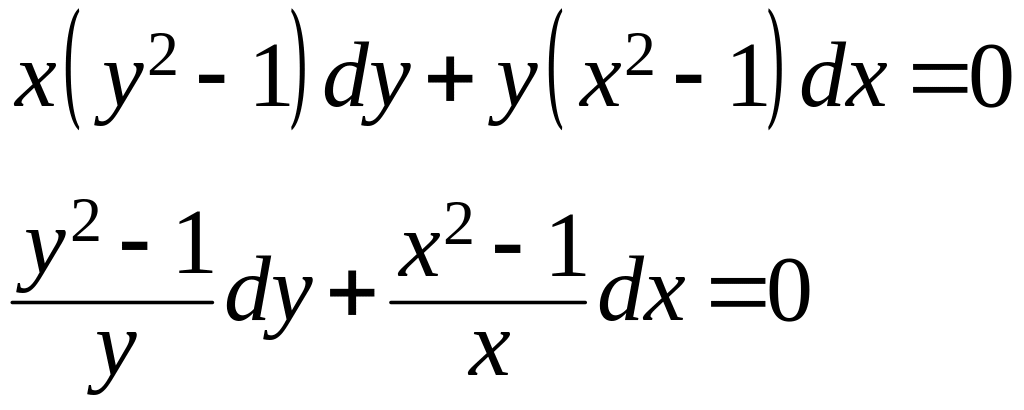
- общее решение.
Пример
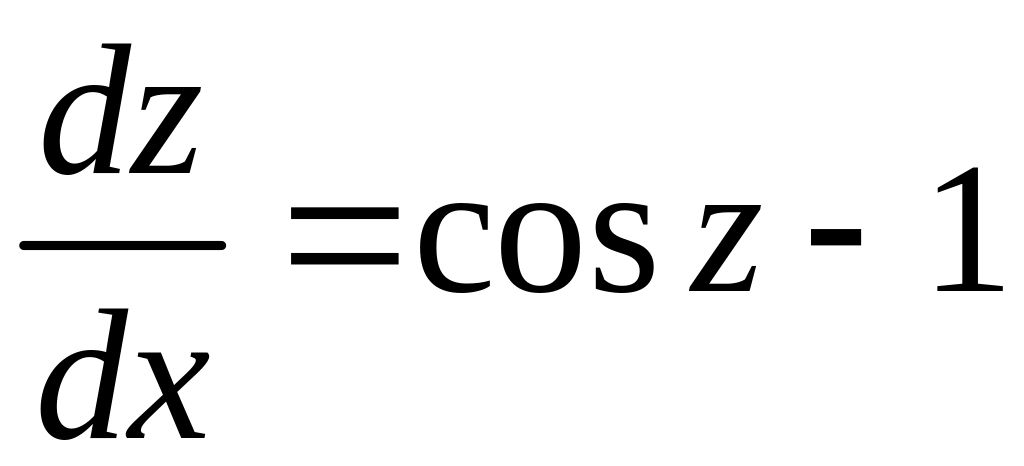
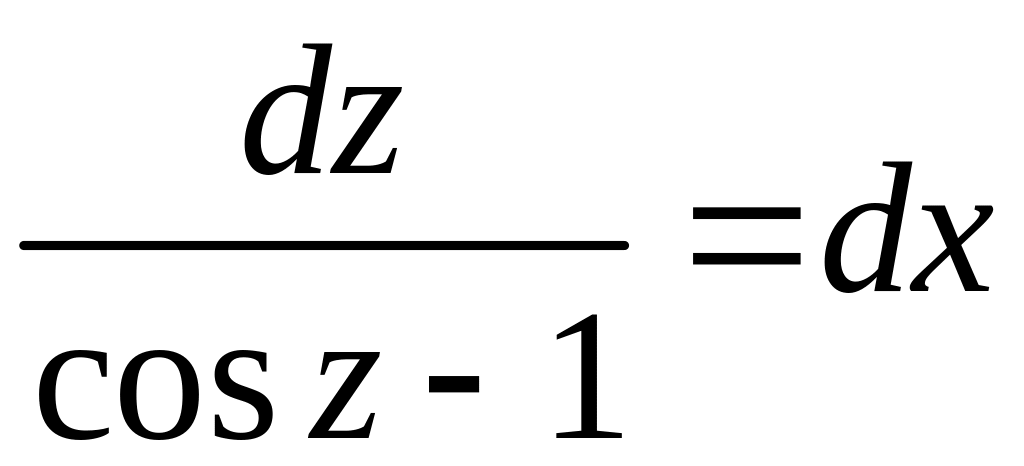
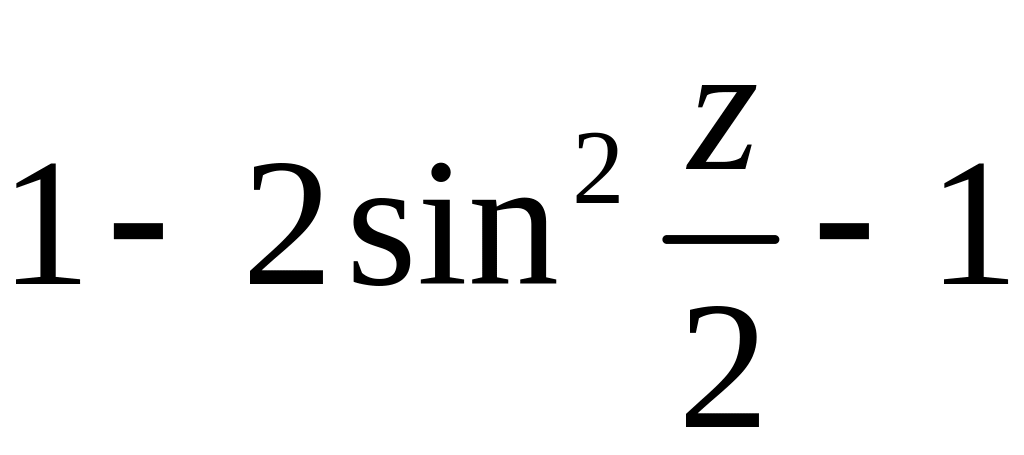
- общее решение.
Однородные уравнения
Дифференциальное уравнение называется однородным, если его можно привести к следующему виду:
сводится к уравнению
с разделяющими переменными.
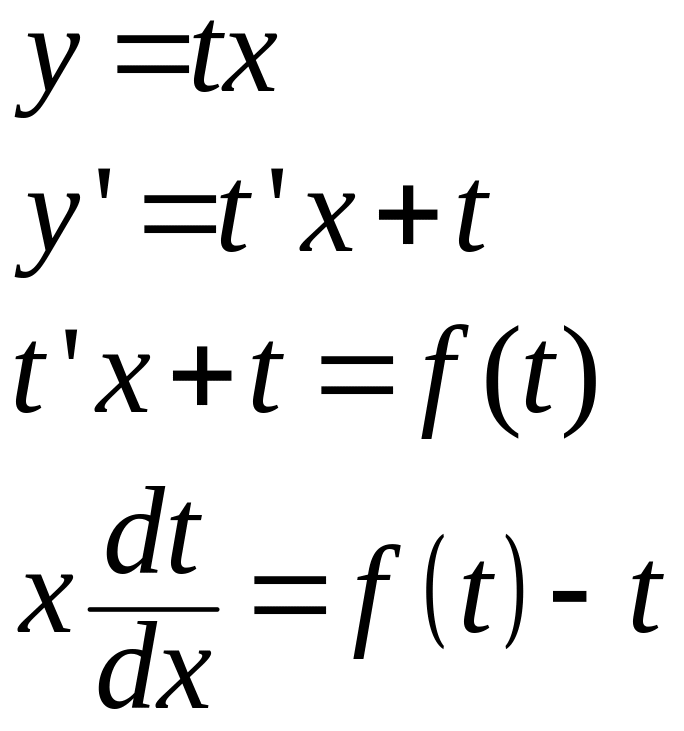
Пример
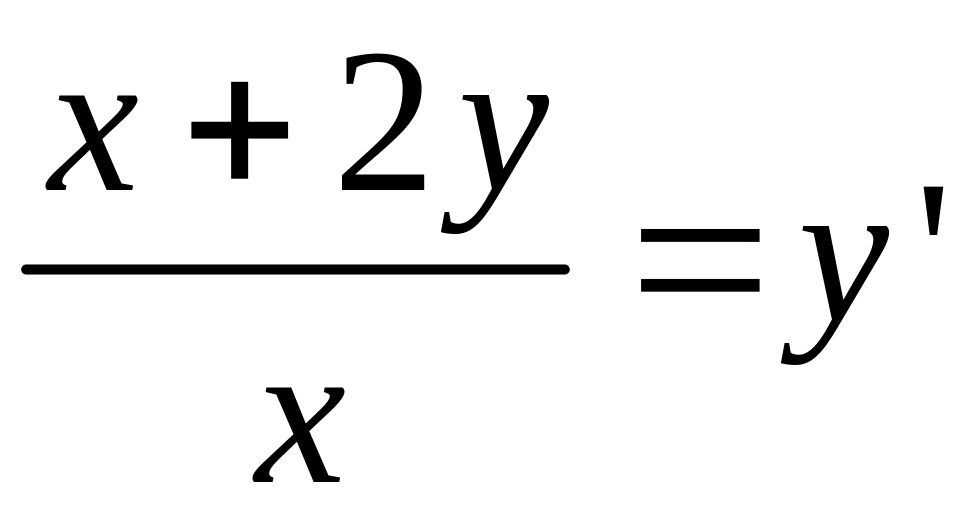
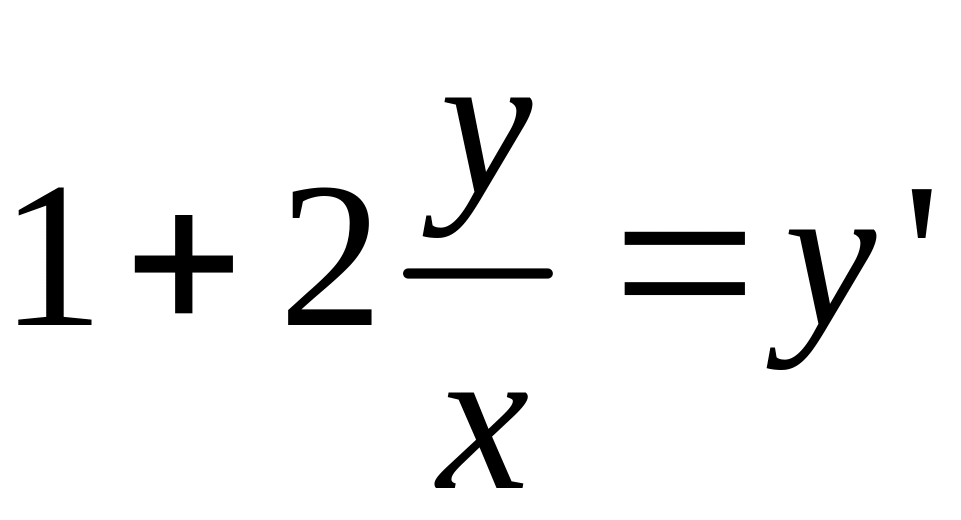
4. Признаки однородности уравнений
Определение
Функция двух переменных называется «к»-однородной функцией, если для любого t выполняется равенство:
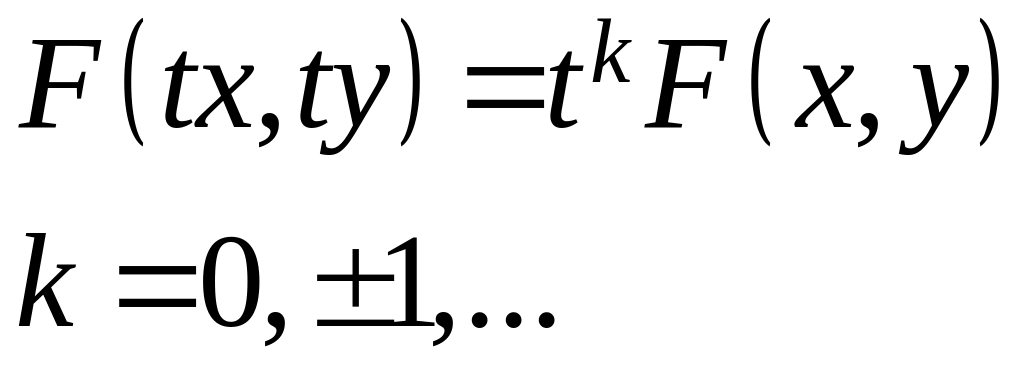
Пример
- однородное степени
«2».
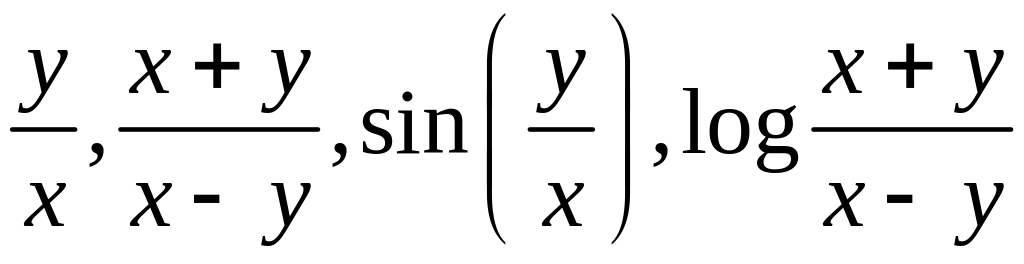- однородные
степени «0».
- однородное.
оно
будет однородным, если Р(х,у) и Q(x,y)
однородные функции одной степени.
Пример
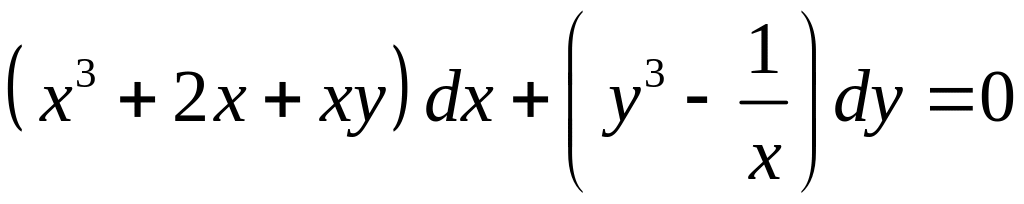
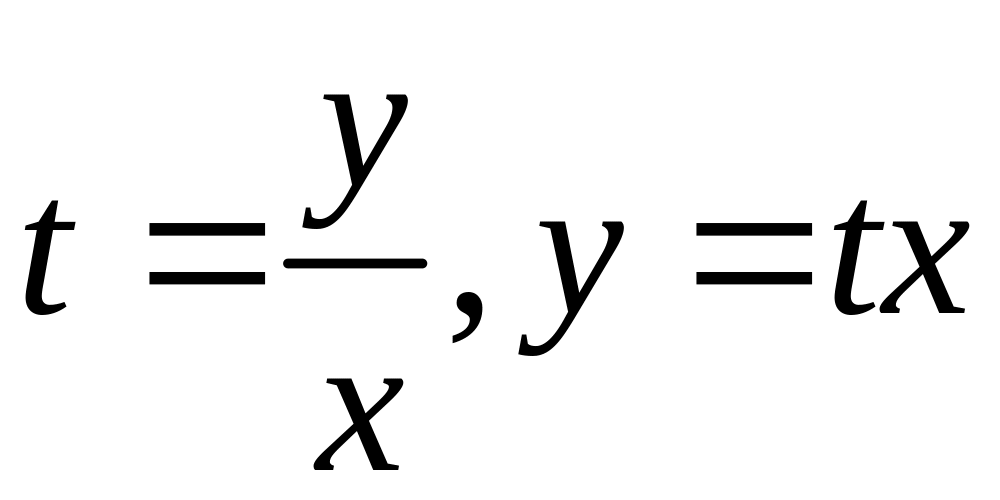
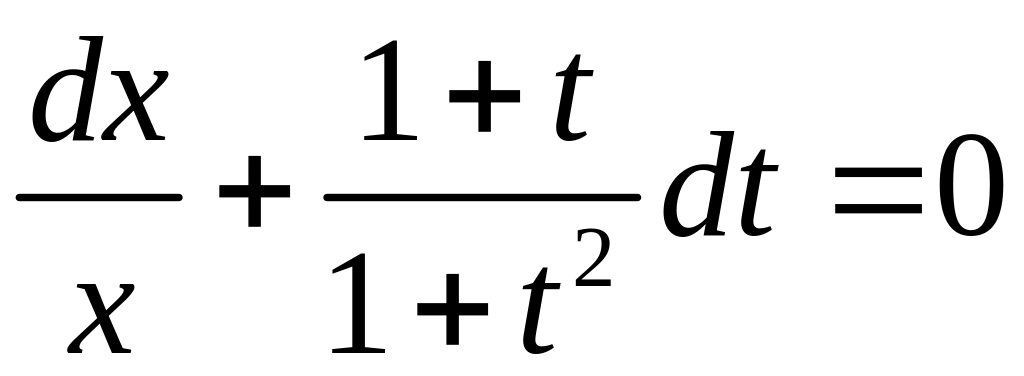
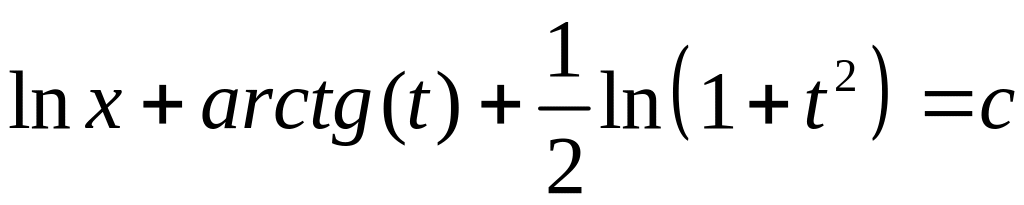
Замечание: поля направлений для однородных уравнений
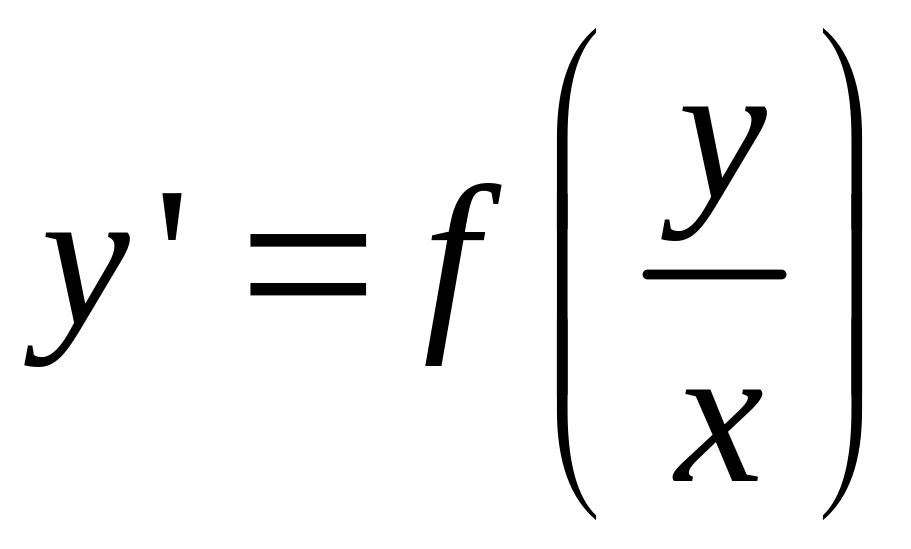
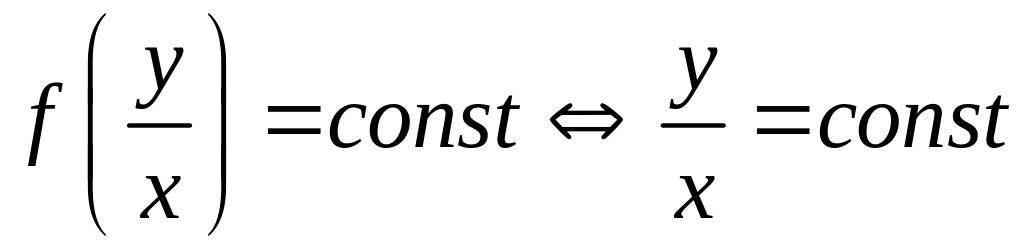
Изоклины, поле направлений постоянно на прямых, выходящих из начала координат. Интегральные прямые подобны относительно начала координат.
Уравнения, сводятся к однородным (квазеоднородным).
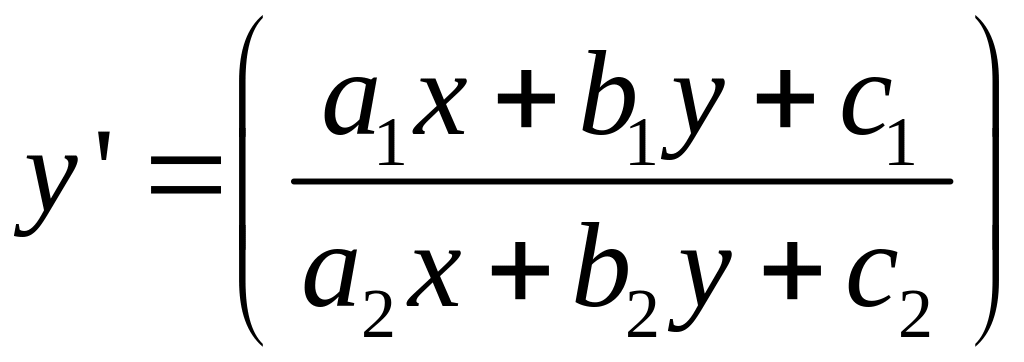
однородные уравнения
a) прямые пересекаются
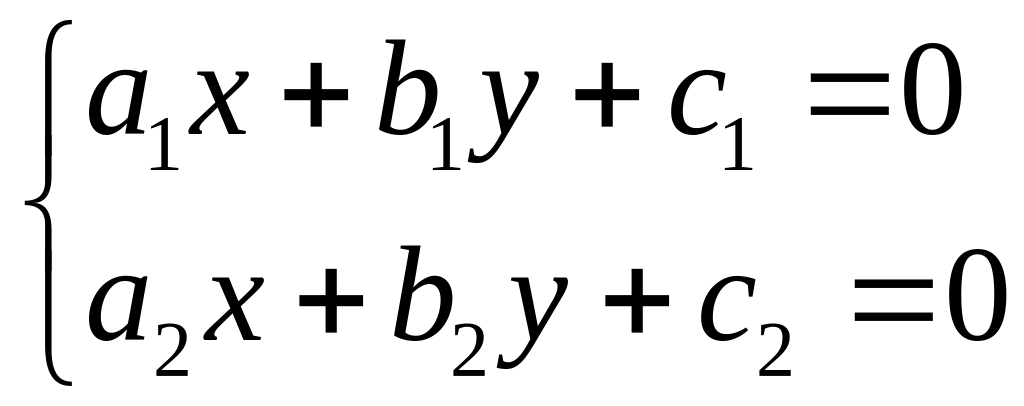
перенесем начало
координат в точку
исчезнут в новых координатах
уравнение
станет однородным
b) прямые не пересекаются
тогда
