- •Мсм как самостоятельная область научных знаний. Их особенности и отличия от методов классич. Статистики.
- •Основные исторические этапы развития мсм.
- •Классификация мсм. Параметрические и непараметрич. Методы, их различия.
- •Особенности социально-экономической информации. Измерение различ. Данных.
- •1) Особенности соц.-экономич. Инф-ции
- •2) Измерение разнотипных данных
- •Оцифровка неколичественной информации. Основные способы оцифровки.
- •2) Таблица логического описания:
- •4) Таблица рангов
- •6) Таблица сравнений:
- •Понятие признакового пространства. Примеры одномерного, двумерного и многомерного признакового пространства. Геометрическая интерпретация.
- •Многомерные случайные величины и их распределения. Многомерные статистические гипотезы. Примеры.
- •1) Понятие многомерной случайной величины (мсв)
- •2) Примеры наиболее часто используемых законов:
- •3) Проверка статистической гипотезы предполагает:
- •Доверительные области
- •Критерий Хотеллинга для двух многомерных выборок.
- •Критерий Бартлетта и проверка гипотезы об однородности дисперсии.
- •Груб. Ошибки. Причины их появл-ия в статистич. Сов-ти. Методы их выявл-ия.
- •Основные методы устойчивого оценивания параметров выбороч. Совокупности.
- •Корреляционно-дисперсионный анализ многомерных количественных данных.
- •Меры связи количественных и неколичественных многомерных данных. Вероятностные коэффициенты связи. Количественные многомерные данные
- •Неколичественные многомерные данные
- •2. Коэффициент Кэндалла
- •Вероятностные коэффициенты связи
- •Дисперсионный и энтропийный коэффициенты конкордации. В каких границах они изменяются, и что это означает.
- •Выборочный коэффициент ранговой корреляции Спирмена и проверка гипотезы о его значимости.
- •Выборочный коэффициент ранговой корреляции Кендалла и проверка гипотезы о его значимости.
- •Критерий независимости для таблиц сопряженности.
- •Метод главных компонент.
- •Использование главных компонент в многомерном регрессионном анализе.
- •33) Кластерный анализ качественных многомерных данных
- •34)Методы иерархического кластерного анализа. Алгоритмическая схема. Геометрическая интерпретация результатов. Основные иерархические методы:
- •3. Метод средних связей
- •Дивизивный метод
- •35)Итеративные методы:
- •39) Вычисление дискриминантных значений. Геометрическая интерпретация результатов. Оценка качества дискриминации.
- •Перечень вопросов по курсу «Многомерные статистические методы»
- •Основные исторические этапы развития мсм.
- •Гауссовское (непрерывное)
- •Общий критерий Хоттелинга:
- •Общий критерий Хоттелинга:
- •Частный критерий Хоттелинга:
- •Одномерный критерий:
- •1.Для количеств.Данных:
- •6 Иерархических методов:
Использование главных компонент в многомерном регрессионном анализе.
Применение метода главных компонент в корреляционно-регрессионном анализе дает исследователю определенные преимущества:
1) Появляется возможность значительного увеличения числа элементарных признаков, участвующих в анализе, при условии введения в регрессию небольшого числа только значимых главных компонент. При этом это не усложняет самой модели и одновременно обуславливает сокращение доли необъясненной дисперсии отклика.
2) Ортогональность главных компонент предотвращает появление эффекта мультиколлинеарности.
Линейное уравнение регрессии на главных компонентах, при условии, что значения отклика (y) измерены в натуральном масштабе, записывается:
![]() или
или
![]() ,
,
Где
- среднее значение зависимой переменной
как оценка свободного член уравнения;
Y
– вектор оценок коэффициентов регрессии
при главных компонентах. Его находят
решением известного матричного
уравнения, минимизирующего сумму
квадратов отклонений:
![]() ;
F
- матрица значений главных компонент
обычного вида размерностью nr.
;
F
- матрица значений главных компонент
обычного вида размерностью nr.
Коэффициенты yir – это некоторые условные единицы, имеющие один масштаб измерения.
Уравнение
регрессии на главных компонентах
эквивалентно регрессии на стандартизированных
значениях признаков:
![]() ,
где
,
где
![]() ;
вектор
- вектор стандартизированных коэффициентов
регрессии.
;
вектор
- вектор стандартизированных коэффициентов
регрессии.
При построении регрессионной модели возникает вопрос об оптимальном составе главных компонент. На практике рекомендуется вначале получить модель с учетом всех m главных компонент, затем с учетом вариации оценки надежности регрессионной модели и колебаний регрессионных коэффициентов число главных компонент может быть уменьшено. Незначимые для регрессии главные компоненты устанавливаются просто, по величине собственных чисел k или в ходе проверки параметров регрессии по t- или F-критериям:
![]() ,
при
,
при
![]() или
или  ,
при
,
при
![]()
Компонента
исключается из регрессии, когда
собственное число k
мало, менее 75 – 90 % и одновременно
несущественно участие k-ой
компоненты в формировании результата
![]() ,
или при низких наблюденных значениях
критериев t
и F.
,
или при низких наблюденных значениях
критериев t
и F.
33) Кластерный анализ качественных многомерных данных
Кластерный анализ - совокупность
методов, позволяющий классифицировать
наблюдения, каждые из которых описывается
либо матрицей объект-признак
(признак-объект) -
![]() ,
либо матрицей предпочтений
,
либо матрицей предпочтений
![]() .
.
Целью кластерного анализа является образование групп схожих между собой элементов, образующих кластеры.
Кластер - группа, класс (англ.); сгусток, гроздь (латынь)
В-первые, кластерный анализ прозвучал в 30х гг в археологии, потом биология и т.д.
Наиболее развитая школа - французская.
В истории кластерный анализ был применен в 2000 г. в книге "Новая история Руси" Фоменко.
Методы кластерного анализа подразделяются на:
I. Иерархические (дерево, графы):
- агломеративные (объединение чего-либо)
- дивизивные (разделение чего-либо)
II. Итеративные (оптимизационные методы)
Входная информация бывает трех типов:
1) матрица объект-признак (если интересует классификация или группировка объекта) или матрица признак-объект (если хотим посмотреть структуру или связи объектов):
2) матрица предпочтений (функционал сопоставления i-го и j-го объектов) (это может быть либо матрицей расстояний, либо матрицей сходства):
3) наличие или ввод обучающей выборки (для блока дивизивных методов)
Она представлена многомерным вектором:
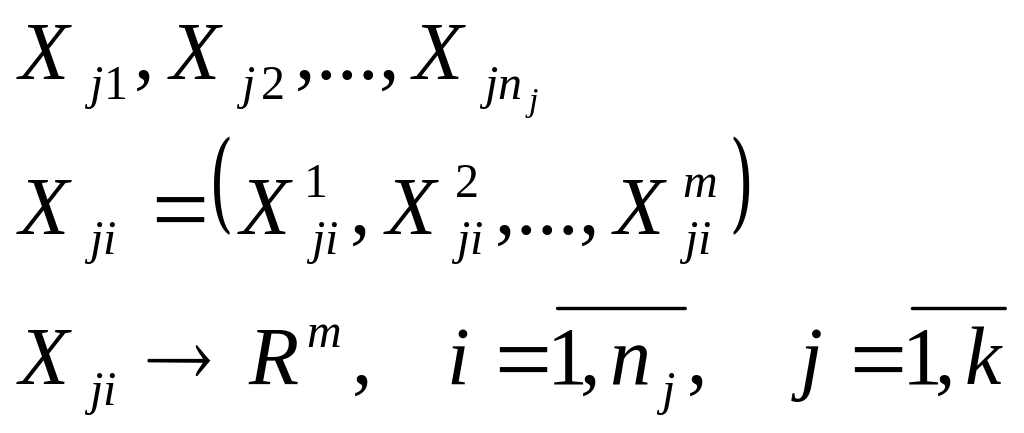 ,
,
Где k – количество групп, кластеров
![]() - количество объектов в j-ом
кластере
- количество объектов в j-ом
кластере
По сути это матрица, которая подгружается в виде либо матрицы , либо матрицы .
На выходе:
Если число кластеров заранее известно, то каждый из n (m) классифицируемых многомерных наблюдений должно быть снабжено адресом (номером кластера)
Если число кластеров и их смысл заранее неизвестен, а выявляется в процессе классификации, то результатом кластерного анализа является разделение множества на однородные в статистическом смысле группы, а определенное их число выбирается нами. Результат выдается в качестве дендраграммы (дерево решений).
Рассмотрим первый тип данных
Нас будет интересовать:
1) Статистическая однородность объектов
2) Схожесть или различия между самими кластерами
3) Выбор целевой функции или оценка качества классификации
![]()
1) Цель - расклассифицировать это
множество объектов на основе матрицы
Х, чтобы образовались подмножества
![]() ,
которые при объединении образуют все
множество объектов. Причем p
должно быть значительно меньше n (
,
которые при объединении образуют все
множество объектов. Причем p
должно быть значительно меньше n (![]() ).
Кроме того каждое
).
Кроме того каждое
![]() содержит объекты однородные в
статистическом смысле. Т.е. если объект
под номером l в статистическом
смысле эквивалентен объекту под номером
k, то они войдут в подмножество:
содержит объекты однородные в
статистическом смысле. Т.е. если объект
под номером l в статистическом
смысле эквивалентен объекту под номером
k, то они войдут в подмножество:
![]()
Если объект l не схож с объектом k, то они образуют разные подмножества. Причем подмножества не должны пересекаться:
![]()
Пример. Оценки студентов по десяти бальной шкале:
![]()
Критериальная функция – минимизация внутригруппового расстояния. В следующих группах оно нулевое:

Чем больше межгрупповое расстояние, тем лучше. Можно взять центры группирования каждой из группировок, найти разницу между этими центрами. Это и будет межгрупповое расстояние.
2) Объекты в кластерном анализе группируются или классифицируются по принципу сходства или различия (выбор метрики). Принцип выбора метрики заключается в том, чтобы она была наиболее информативной для измерения различия ваших объектов.
1. Если данные количественные, то чаще всего используют
- Метрику Минковского, которая базируется на принципе расстояний:

Если p = 1 – линейное (Хевингово) расстояние
Если p = 2 – Эвклидово расстояние
Если p = 3 – квадрат- Эвклидово расстояние
- Расстояние Махаланобиса:
![]() ,
,
Где
![]() - матрица весов в многомерном пространстве,
она позволяет взвешивать каждый признак
и получать более точное расстояние
- матрица весов в многомерном пространстве,
она позволяет взвешивать каждый признак
и получать более точное расстояние
2. Если мы работаем с неколичественными данными, то использовать предыдущие методы не информативно. Сначала нужно сформировать матрицу . В частности, если качественные признаки, то матрица сходства формируется:
1) по Спирману:
![]()
2) по Кендаллу
3) Коэффициент сходства
П ример:
ример:
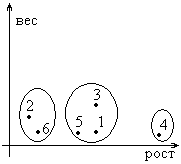
Задана матрица расстояний для следующих объектов (4 девочки и 2 мальчика) в двумерном признаковом пространстве (рост и вес):
![]()
1 шаг. Из матрицы расстояний ищутся наиболее близкие объекты:
![]()

2 шаг. Редуцируем матрицу расстояний, исключаем из рассмотрения первого мальчика и пятую девочку. Опять находим минимальные расстояния:
![]()
3 шаг. Остается матрица 22.
но мы видим, что третья и четвертая
девочки различны (расстояние максимально).
Их можно отнести либо в отдельные
кластеры, либо в уже существующие
кластеры:
шаг. Остается матрица 22.
но мы видим, что третья и четвертая
девочки различны (расстояние максимально).
Их можно отнести либо в отдельные
кластеры, либо в уже существующие
кластеры:
![]()
Т.к.
![]() и
и
![]() ,
то 3-ий объект ближе к элементам первого
кластера, чем 4-ый.
,
то 3-ий объект ближе к элементам первого
кластера, чем 4-ый.
Т.к.
![]() и
и
![]() ,
следовательно, 3-ий объект ближе к
элементам первого кластера, чем к
элементам второго кластера, а 4-ый
элемент отнесем к отдельной группе.
,
следовательно, 3-ий объект ближе к
элементам первого кластера, чем к
элементам второго кластера, а 4-ый
элемент отнесем к отдельной группе.
4 шаг. Итак, мы получили три кластера:
![]()
![]()
![]()
Графически это можно представить в виде: