12. Знакопеременные ряды. Абсолютная и условная сходимость.

Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.

Теорема1. Если знакопеременный ряд таков, что ряд, составленный из абсолютных величин его членов 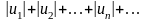сходится, то и данный знакопеременный ряд также сходится.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.

13 Теорема Лейбница:

Если в з/ч ряде абсолютные величины членов ряда убывают, и общий их член →0, то ряд сходится, причем его сумма по общей величине меньше первого члена ряда, а остаток ряда по модулю меньше первого из отбрасываемых членов. Док-во. Рассмотрим частичную сумму ряда с номером 2N:  и заметим, что   , т.к. по условию 1 имеем нер-во: . .

14. Знакочередующиеся ряды. Теорема Лейбница.

Теорема Лейбница:

Если в знакочередующемся ряду 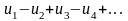, где 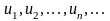положительны, члены таковы, что 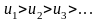и , то ряд сходится, его сумма положительна и не превосходит первого члена.

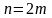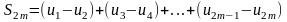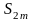Доказательство: Рассмотрим сумму первых членов ряда. По условию 1 выражение в каждой скобке положительно. Следовательно, сумма положительна и возрастает с возрастанием m. Запишем теперь эту же сумму так:

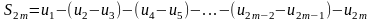По условию 1 каждая из скобок положительна. Поэтому в результате вычитания этих скобок из 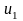мы получим число, меньшее . Таким образом, мы установили, что при возрастании m возрастает и ограничена сверху. Отсюда следует, что имеет предел S

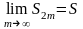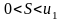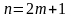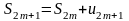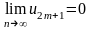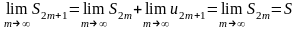, причем . Однако сходимость еще не доказана. Мы доказали только, что последовательность четных частичных сумм имеет пределом число S. Докажем теперь, что нечетные частичные суммы также стремятся к пределу S. Рассмотрим для этого сумму первых членов исходного ряда. . Так как по условию 2 теоремы , то следовательно Тем самым мы доказали, что как при четном n, так и при нечетном. Следовательно, исходный ряд сходится.

! Теорема Лейбница справедлива, если условия выполняются с некоторого N.

15. Функциональные ряды, область сходимости. Равномерная сходимость. Признак Вейерштрассе.

Ряд называется функциональным, если его члены являются функциями от х.

Совокупность тех значений х, при которых функциональный ряд сходится, называют областью сходимости этого ряда.

Функциональный ряд называется равномерно сходящимся на отрезке [a; b], если для любого сколь угодно малого 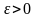найдется такой номер N, что при всех будет выполняться неравенство 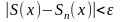для любого х их отрезка [a; b].

Признак Вейерштрассе.

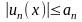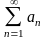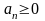Пусть есть функциональный ряд. Если для него справедливо неравенство и числовой ряд при сходится в некоторой области D, то в этой области ряд сходится равномерно.