6 Некоторые очевидные свойства числовых рядов:

1)Теорема 1. На сходимость ряда не влияет отбрасывание конечного числа его членов.

Док-во: S_n – сумма n первых членов ряда, C_k – сумма k отброшенных членов, D_n-k – сумма членов ряда, входящих в сумму S_n и не входящих в C_k. Тогда имеем: S_n=C_k+D_n-k, где C_k – постоянное число, не зависящее от n. Из последнего соотношения следует, что если сущ-ет limD_n-k, то сущ-ет и limS_n; если сущ-ет lim S_n, то сущ-ет limD_n-k, а это доказ-ет справедливость теоремы.

2)Теорема 2. Если ряд a₁+a₂+...(1) сходится, и его сумма равна S, то ряд ca₁+ca₂+...(2), где c=const, также сходится и его сумма равна сS.

Док-во: обозначим n-ю частичн сумму ряда (1) через S_n, а ряда (2) – через D_n. Тогда D_n=ca₁+...+ca_n=c(a₁+...+a_n)=cS_n. Отсюда ясно, что передел n-ой частичной суммы ряда (2) сущ-ет, т.к.

lim D_n=lim(cS_n)=climS_n=cS. ч.т.д.

3)Теорема 3. Если ряды a₁+a₂+...(5) и b₁+b₂+...(6) сходятся, и их суммы, соответственно, равны S₁и S₂, то ряды (a₁+b₁)+(a₂+b₂)+...(7) и (a₁–b₁)+(a₂–b₂)+...(8) также сходятся, и их суммы, соответственно, равны S₁+S₂ и

S₁–S₂.

Док-во: док-ем сходимость ряда (7). Обозначая его n-ую частичную сумму через D_n, а n-е частичные суммы рядов (5) и (6) соответственно через S_1n и S_2n, получим: D_n=(a₁+b₁)+...+(a_n+b_n)=(a₁+...+a_n)+(b₁+...+b_n)=S_1n+S_2n. Переходя к в этом равенстве к пределу при n, получим limD_n=lim(S_1n+S_2n)= limS_1n+limS_2n=S_1n+S_2n.

Т.о., ряд (7) сходится и его сумма равна S_1n+S_2n.

4)Необходимый признак сходимости ряда. Если ряд сходится, то limU_n=0 n.

Док-во: пусть ряд U₁+U₂+...+U_n+... сходится, т.е. limS_n=S n, тогда имеет место равенство limS_n-1=S.

limS_n–limS_n-1=0, lim(S_n–S_n-1)=0. Но S_n–S_n-1=U_n следов-но lim U_n=0 ч.т.д.

7. Интегральный признак Коши.

Пусть члены ряда положительны и не возрастают, то есть 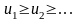и пусть f(х) – такая непрерывная не возрастающая функция, что , , .

Тогда справедливы следующие утверждения:

если несобственный интеграл сходится, то сходится и исходный ряд;

если указанный интеграл расходится, то расходится и исходный ряд.

Доказательство:

1) Предположим, что интеграл сходится, то есть имеет конечное значение. Так как , то , то есть частичная сумма Sn остается ограниченной при всех значениях n. Но при увеличении n она возрастает, так как все члены u_n положительны. Следовательно, Sn при имеет конечный придел , то есть ряд сходится.

2) Предположим далее, что . Это значит, что неограниченно возрастает при возрастании n. Но тогда Sn также неограниченно возрастает при возрастании n, то есть ряд расходится.

8. Признаки сравнения. Признак Даламбера.

Обычный признак сравнения.

Пусть имеем два ряда с положительными членами

(1) и (2), для которых выполняется условие: . Тогда из сходимости ряда 2 следует сходимость ряда 1;

из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

Имеем два ряда (1) и (2).

. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :

1) ряд сходится

2) ряд расходится.

Признак Даламбера.

Если в ряду с положительными членами отношение (n + 1)-го члена к n-му при имеет конечный предел l, то есть , то

ряд сходится в случае ;

ряд расходится в случае ;3) в случае ответа о сходимости или расходимости ряда теорема не дает.

9 Предельный признак сравнения.

Если сущ-ет limU_n/V_n=L, но L0, при n, то ряды ведут себя одинаково.

10. Признаки сравнения. Признак Даламбера.

Обычный признак сравнения.

Пусть имеем два ряда с положительными членами

(1) и (2), для которых выполняется условие: . Тогда из сходимости ряда 2 следует сходимость ряда 1;

из расходимости ряда 1 следует расходимость ряда 2.

Предельный признак сравнения.

Имеем два ряда (1) и (2).

. Если L существует, то оба ряда сходятся одновременно.

Пусть ряд 2 сходится, тогда по обычному признаку сравнения сходится и ряд 1.

Имеем ряд :

1) ряд сходится

2) ряд расходится.

Признак Даламбера.

Если в ряду с положительными членами отношение (n + 1)-го члена к n-му при имеет конечный предел l, то есть , то

ряд сходится в случае ;

ряд расходится в случае ;

3) в случае ответа о сходимости или расходимости ряда теорема не дает.

11 Радикальный признак Коши.

Если для ряда с положительными членами величина имеет конечный предел l при , то есть , то

в случае ряд сходится;

в случае ряд расходится;

3) в случае ответа о сходимости или расходимости ряда теорема не дает.

Доказательство:

Пусть . Рассмотрим число q, удовлетворяющее соотношению 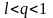. Начиная с некоторого номера n=N будет иметь место соотношение . Отсюда следует, что или для всех . Рассмотрим теперь два ряда: (1) и (2). Ряд 2 сходится, так как его члены образуют убывающую геометрическую прогрессию. Члены ряда 1, начиная с , меньше членов ряда 2. Следовательно, ряд 1 сходится.

Пусть . Тогда, начиная с некоторого номера n=N будем иметь или . Но если все члены рассматриваемого ряда, начиная с , больше 1, то ряд расходится, так как его общий член не стремится к нулю.