Метод Зейделя для решения слау
Рекуррентное соотношение Якоби (2.2) можно несколько улучшить, если найденные при выполнении текущей итерации значения неизвестных сразу подставлять в правую часть выражения:
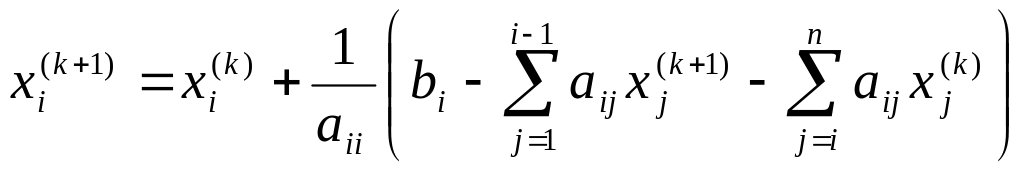(2.11)
Такой процесс называется
методом Зейделя или методом последовательных
смещений. Векторы
и
в преобразовании (2.5) теперь будут иметь
вид
;
.
В случае преобладания диагональных элементов, согласно условия (2.7) метод Зейделя сходится быстрее, чем метод Якоби.
Метод
Зейделя можно рассматривать как частный
случай метода релаксации, в котором для
улучшения сходимости вводится параметр
:
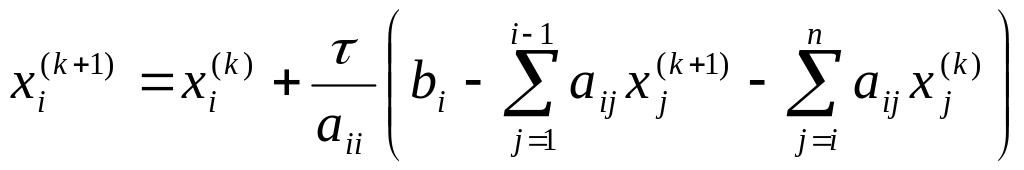(2.12)
при
это нижняя релаксация, а при
-
верхняя релаксация. Метод Зейделя
соответствует случаю
.
Реализуем метод Зейделя в Excel. Рассмотрим методику на примере системы .
В качестве начального значения взято . Заданная точность =0,00001. Дальнейшее вычисление приведем в виде таблицы.
Таблица 2.1. Вспомогательная таблица для вычисления корней системы методом Зейделя
-
k
x1k
x2k
x3k
max|xik+1-xik|
0
1
0
1
-
1
2,33333
0,83333
0,83333
1,33333
2
2,00000
1,04167
1,01389
0,20833
3
1,99074
1,00116
1,00347
0,00926
4
2,00077
0,99875
0,99932
0,01003
5
2,00019
1,00007
0,99996
0,00133
6
1,99996
1,00003
1,00002
0,00006
7
2,00000
1,00000
1,00000
0,00004
8
2,00000
1,00000
1,00000
0,00000
Оценим число арифметических операций, выполняемых в итерационном процессе. Запишем фрагмент процедуры на языке Паскаль:
Kmax:=100; key:=false;
repeat
inc (k);
for i:=1 to n do
begin s:=b[i];
for j:=1 to n do s:=s - a[i,j]*x[j];
s:=s*tau/a[i,i]; x[i]:=x[i]+s;
end;
if abs (S)>eps
then key:=true;
until (not key) or (k=kmax);
где k-
число итераций, n-размер
матрицы
.
Видно, что для достижения заданной
точности необходимо порядка
операций.
Число итераций, необходимых для получения заданной точности , можно вычислить из так называемой априорной оценки погрешности (a priori- до опыта):
(2.13)
Действительно
,
откуда
(2.14)
Можно получить апостериорную (a posteriori – из опыта) оценку погрешности:
(2.15)
Апостериорная погрешность точнее априорной и ее можно использовать как еще один критерий завершения процесса итерации:
(2.16)
В
заключение сделаем важное для приложений
замечание. Метод Зейделя сходится для
нормальных систем, т.е. систем, для
которых матрица
- симметричная и положительно определенная.
Получить такую систему можно, умножив
систему (1.1) на транспонированную матрицу
,
тогда
(2.17)
является нормальной системой.