3. Задания для самостоятельной работы

Дана система линейных алгебраических уравнений:

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

4. Составить и провести отладку решения СЛАУ методом Якоби.

5. Провести тестовые расчеты, в которых выполнялись бы условия сходимости (2.6) и (2.7) .

6. Для заданного значения точности провести расчеты с разными критериями остановки итерационного процесса. Сравнить необходимое при этом число итераций.

7. Провести расчеты для двух выбранных критериев остановки, но разных значений точности . Сравнить количество итераций.

8. Вычислить число требуемых итераций из априорной оценки погрешности (2.14) и сравнить со значениями, полученными из эксперимента.

9. Сравнить так же результаты расчетов, полученные при решении плохо обусловленных систем методами Гаусса и Якоби.

10. Составить и провести отладку подпрограмм для решения СЛАУ методом Зейделя. Выполнить все пункты задания 2.

11. Сравнить результаты, полученные методами Якоби и Зейделя.

12. Сравнить эти результаты с полученными в предыдущей работе прямыми методами решения систем уравнений.

13. Реализовать в виде отдельных процедур алгоритм нормирования СЛАУ. Провести тестовые расчеты. Выполнить анализ полученных результатов.

14. Дополните свой модуль подпрограмм линейной алгебры подпрограммами, реализующими итерационные стратегии.

5. Контрольные вопросы

1. Каковы условия сходимости итерационных методов?

2. Методы преобразования системы 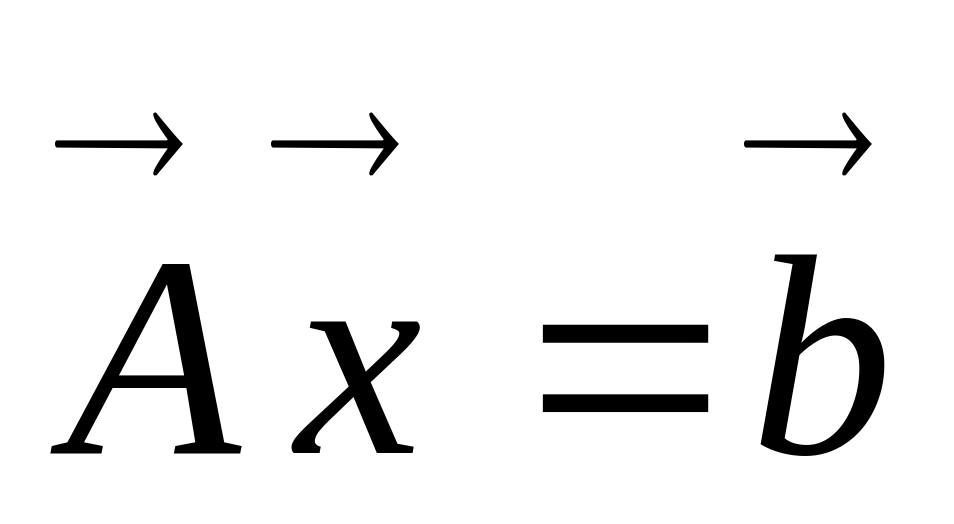к виду .

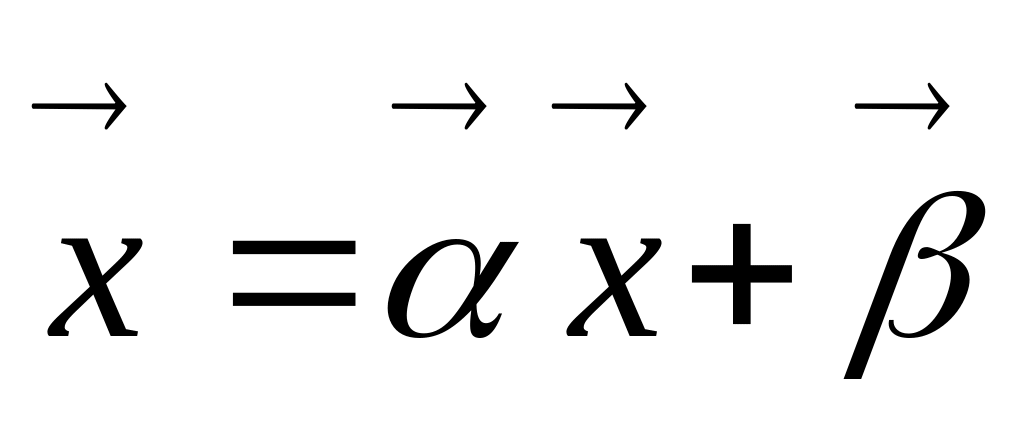3. Методика решения СЛАУ по методу Якоби.

4. Методика решения СЛАУ по методу Зейделя.

5. Сравнение итерационных методов решения СЛАУ.

6. Вычислите числа итераций априорным методом.

7. Оценка погрешности апостериорным методом.

Лабораторно-практическая работа 3

Численные методы решения нелинейных уравнений

1. Введение

Рассмотрим задачу нахождения корней нелинейного уравнения

f(x)=0 (3.1)

Корнями уравнения (3.1) называются такие значения х, которые при подстановке обращают его в тождество. Только для простейших уравнений удается найти решение в виде формул, т.е. аналитическом виде. Некоторые из таких уравнений подробно изучались в школьном курсе математики. Чаще приходится решать уравнения приближенными методами, наибольшее распространение среди которых, в связи с появлением компьютеров, получили численные методы. В этой работе познакомимся с некоторыми из них.

Алгоритм нахождения корней приближенными методами можно разбить на два этапа. На первом изучается расположение корней и проводится их разделение. Находится область [a,b], в которой существует корень уравнения или начальное приближение к корню x₀. Простейший способ решения этой задачи является исследование графика функции f(x) . В общем же случае для её решения необходимо привлекать все средства математического анализа.

Существование на найденном отрезке [a,b], по крайней мере, одного корня уравнения (3.1) следует из условия Больцано:

f(a) * f(b) < 0 (3.2)

При этом подразумевается, что функция f(x) непрерывна на данном отрезке. Однако данное условие не отвечает на вопрос о количестве корней уравнения на заданном отрезке [a,b]. Если же требование непрерывности функции дополнить ещё требованием её монотонности, а это следует из знакопостоянства первой производной , то можно утверждать о существовании единственного корня на заданном отрезке.

При локализации корней важно так же знание основных свойств данного типа уравнения. К примеру, напомним, некоторые свойства алгебраических уравнений:

, (3.3)

где вещественные коэффициенты.

а) Уравнение степени n имеет n корней, среди которых могут быть как вещественные, так и комплексные. Комплексные корни образуют комплексно-сопряженные пары и, следовательно, уравнение имеет четное число таких корней. При нечетном значении n имеется, по меньшей мере, один вещественный корень.

б) Число положительных вещественных корней меньше или равно числа перемен знаков в последовательности коэффициентов . Замена х на –х в уравнении (3.3) позволяет таким же способом оценить число отрицательных корней.

На втором этапе решения уравнения (3.1), используя полученное начальное приближение, строится итерационный процесс, позволяющий уточнять значение корня с некоторой, наперед заданной точностью . Итерационный процесс состоит в последовательном уточнении начального приближения. Каждый такой шаг называется итерацией. В результате процесса итерации находится последовательность приближенных значений корней уравнения . Если эта последовательность с ростом n приближается к истинному значению корня x , то итерационный процесс сходится. Говорят, что итерационный процесс сходится, по меньшей мере, с порядком m, если выполнено условие:

, (3.4)

где С>0 некоторая константа. Если m=1 , то говорят о сходимости первого порядка; m=2 - о квадратичной, m=3 - о кубической сходимостях.

Итерационные циклы заканчиваются, если при заданной допустимой погрешности выполняются критерии по абсолютным или относительным отклонениям:

; (3.5,3.6)

или малости невязки:

(3.7)

Эта работа посвящена изучению некоторых класических алгоритмом решения нелинейных уравнений, их скоростей сходимости, влиянию на сходимость выбора начального приближения и другим вопросам.