6. Задания для самостоятельной работы

1. Используя методы численного дифференцирования и приближенные методы решения уравнений найти значение производной в указанной точке :

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

25. 

2. Провести численно оценку погрешностей вычислений.

7. Контрольные вопросы

1. Суть проблемы приближенного дифференцирования.

2. Как используют полином Ньютона (для равномерной сетки) при вычислении значений производных функций?

3. Как можно вычислить приближенное значение производной функции, основываясь на определении производной?

4. Запишите основные формулы вычисления производной, использующие сеточные значения.

5. Дайте сравнительную характеристику точности получаемых результатов в зависимости применяемой формулы приближенного дифференцирования.

Лабораторно-практическая работа 7

Численное интегрирование

1. Введение

При вычислении площадей, объемов и решении многих других задач приходится сталкиваться с проблемой интегрирования. Если не удается аналитически выразить первообразную функцию или подынтегральная функция задана таблично, применяются приближенные и, в первую очередь, численные методы вычисления интегралов.

Идея численного интегрирования заложена в определении интеграла Римана от функции f(x):

, (7.1)

где (7.2)

интегральная сумма, - произвольная точка на частичном интервале , - длина интервала, , причем .

Интегральную сумму (7.2) называют квадратурной формулой; точки , в которых вычисляются значения функции f(x), - узлами; - весами квадратурной формулы. Разность является погрешностью квадратурной формулы, зависящей как от выбора весов, так и расположения узлов.

Разнообразные формулы численного интегрирования отличаются, главным образом, способом выбора узлов и весов. В этой работе будут рассмотрены методы прямоугольников, трапеций и парабол, построенные на равномерном выборе шаге h=const, способы их модификаций, а также алгоритмы вычисления интегралов со специально выбранными узлами и весами.

2. Метод прямоугольников

Заменим площадь под функцией f(x) на отрезке площадью прямоугольника, тогда интеграл на этом частичном отрезке легко вычисляется:

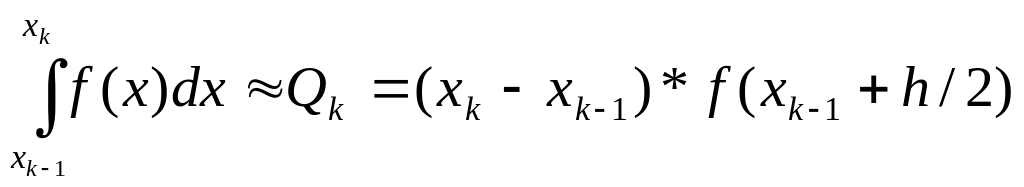(7.3)

Часто это соотношение называется формулой средней точки. Интеграл на всем интервале [a,b] при равномерном выборе шага

(7.4)

Погрешность этой формулы

(7.5)

где . Такая квадратурная формула имеет второй порядок точности .

Если узлы расположены справа или слева, т.е.

; , (7.6)

то, из-за нарушения симметрии, погрешность этих формул становиться на порядок меньше

Составим подпрограмму-функцию:

function Q_Mp( a,b:real; n:longint): real;

var s,h:real; k:longint;

begin

h:=(b-a)/n; s:=0;

for k:=1 to n do s:=s +f(a+h*(k-0.5));

Q_Mp:=h*s

end;

Заметим, что узлы на интервале [a,b] могут быть выбраны случайным образом. Проведя n вычислений со случайными узлами , усредним результат, который принимается за приближенное значение интеграла

, (7.7)

где - среднее на интервале [a,b] значение подынтегральной функции, . Здесь - случайное число, равномерно распределенное на интервале [0,1], которое можно моделировать на языке Turbo Pascal с помощью датчика Random.

Погрешность такого статистического варианта метода прямоугольников, называемого еще методом Метрополиса (частного случая метода Монте-Карло), уменьшается с ростом числа испытаний по закону . Однако этот метод можно обобщить для вычисления кратных интегралов, а так же моделирования многих других задач.