
- •1.Скалярное произведение векторов.
- •5.Касат.И норм. Плоск. В задан. Т.
- •6.Длина дуги кривой.
- •7. Сопровождающ. Трехгран. Кривой.
- •8. Нахожд. Эл-ов сопр-щего 3-хгран. В произвольн. Параметризации
- •9. Формулы Френе. Кривизна и кручение кривой.
- •10.Нахождение кривизны и кручения кривой в произвол. Параметризации.
- •15. Предел и непрерывность
15. Предел и непрерывность
Пусть задана функция z=f(x,y), р(х,у)-текущая точка, р0(х0,у0)- рассматриваемая точка. Опр. Окрестностью точки р0 называется круг с центром в точке р0 и радиусом r. r = Ö(х-х0)2+(у-у0)2ØЧисло А называется пределом функции |в точке р0, если для любого
Lim f(x,y)pàp0 сколь угодно малого числа e можно указать такое число r (e)>0, что при всех значениях х и у, для которых расстояние от т. р до р0 меньше r выполняется неравенство: ½f(x,y) - А½<e, т.е. для всех точек р, попадающих в окрестность точки р0, с радиусом r, значение функции отличается от А меньше чем на e по абсолютной величине. А это значит, что когда точка р приблизится к точке р0 по любому пути, значение функции неограниченно приближается к числу А. Непрерывность функции.
Пусть задана функция z=f(x,y), р(х,у)-текущая точка, р0(х0,у0)- рассматриваемая точка.
Опр. Функция z=f(x,y) называется непрерывной в т. р0, если выполняются 3 условия:
1)функция определена в этой точке. f(р0) = f(x,y); 2)ф-я имеет предел в этой точке.
Lim f(р) = bpàp0 3)Предел равен значению функции в этой точке: b = f(x0,y0);
Lim f(x,y) = f(x0,y0); pàp0
Если хотя бы 1 из условий непрерывности нарушается, то точка р называется точкой разрыва. Для функций 2х переменных могут существовать отдельные точки разрыва и целые линии разрыва.
Понятие предела и непрерывности для функций большего числа переменных определяется аналогично.
16-17. Частные производные функции z - f(x, у), их геометрический смысл.
Правило нахождения частных производных: частноя производная по рассматриваемой переменной ищется как обычная производная функции одной этой переменной, остальные переменные расстатриваются как постоянные величины. При этом оказываются справедливыми все формулы дифференцирования функции одной переменной (производноя суммы, произведения, частного). Частные производные. Частной производной ф. нескольких переменных по одной из этих переменных н. предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если это предел существ.)
Нахождение произв.z’x н. дифферинцир. ф. z по аргум. x, а точка (x0,y0) н. точкой дифференцирования. Т.о. частные произв. ф. 2 аргум. по одному из них – это самые обычные произв. той ф. одной переменной, котор. Получается из нашей ф. при закреплении др. аргум.
18. Полный диф. функции z = f(x, у).
z=f(x,y) в области D.
p(x,y) Î D - рассматриваемая точка. Дадим х приращение Dх, у - Dу. Получим р1(х+Dх, у+Dу). Вычилим значение функции. Полным приращение функции называется разность:
Dz = f(p1)-f(p)
Dz = f(x+Dx,y+Dy) - f(x,y)
Опр. Полным дифференциалом функции z=f(x,y) называется главная линейная часть приращения этой функции, если приращение можно преобразовать к виду: Dz = ADx + BDy + a А, В - не зависят от Dх, Dу; a - зависит от Dх и Dу и при этом Lim a = 0
r®0
r - расстояние между точками р и р1
S = рр1 = ÖDх2 +Dу2Øa является бескон. малой, более высокого порядка, чем r
При ументшении Dх и Dу a®0 быстрее, чем r. Из определ. следует, что полный диф. Ф. равен z = ADx + BDy
При малых Dх и Dу имеет место равенство Dz » dz.
Опр. Если функция z=f(x,y) имеет полный дифференциал в точке р, то она называется дифференцируемой в этой точке.
Теорема. Необходим. Услов. Диф.Ф.
Если функция z=f(x,y) диф. в точке р, то она имеет частные производные в этой точке и при этом выражение поного дифференциала А = ¶z/¶x B = ¶z/¶y, т.е. полный дифференциал может быть записак в виде:
dz = ¶z/¶x Dx + ¶z/¶y Dy
Док-во: По определению дифференцируемости приращение функции может быть записано в виде:
Dz = ADx+BDy +a при любом Dх и Dу.
Рассмотрим 2 частных случая
1)Dх¹0 Dу = 0
При этом Dz=ADx+a /Dx и перейдем к пределу. Полное приращение функций превращается в частное приращение.
Lim Dxz/Dx = Lim A+a/Dx
Dx®0 Dx®0
¶z/¶x= A+Lim(Dx®0)a/Dx =0 т.к. r=Dх
В результате получаем А=¶z/¶x
2)Dx=0 Dy¹0
При этом аналогичным образом получим, что В=¶z/¶y
Теорема доказана. Как следствие à полный дифференциал диффер. функции определяется по формуле:
dz=¶z/¶x·Dx+¶z/¶y·Dy, если при этом учесть, сто приращение независимых переменных х и у равны их диффер. Dx=dx, Dy=dy, то окончательно получим:
dz=¶z/¶x·dx+¶z/¶y·dy
Теорема 2. Достаточное условия диффер. функции. Если z=f(x,y) имеет в точке р(х,у) непрерывные частные производные, то она дифференцируема в этой точке, т.е. она имеет полный дифференциал.
19. Применение полного диф-ла ф-ии Z=f(x,y) в приближ. вычисл. Z=f(x,y), чтобы найти знач. ф-ии в точке (х,у) выбир. ближ. знач.(х,у) к заданным, т.е. т. (х0,у0), для котор. знач. ф-ии легко найти, затем дают приращ. Δх и Δу, так чтобы х=х0+Δх, у=у0+Δу, тогда ΔZ=f(x0+Δx,y0+Δy)-f(x0,y0), тогда f(x,y)= ΔZ+f(x0,y0), но полное приращ. ф-ии в кач-ве своей главной линейной части содерж. диф-ал и поэт. ΔZ прибл. равно знач. диф-а dZ. f(x,y)=dZ+f(x0,y0), где dZ в т.(x0,y0). Геом. смысл: полный диф. данной ф-ии представл. собой приращ. этой ф-ии до касат. пл-ти, провед. через точку (x,y,f(x,y)), если х и у даны приращ. Δx и Δy.
20.Производная по направл. для ф-ии Z=f(x,y).Известно, что ф-ия Z=f(x,y) в обл. своего определ. задаёт некот. скалярное поле. Выберем в этой обл. т. М и зададим направл. в обл. опред. Если от выбр. М перемест. В др. т. Этой области, то знач. Скал. Поля измен. Рассм. в данной обл. т.М, так чтобы вектора ММ1↑↑l,при перемещ. Из М в М1 скаляр. поле меняется на велич. Δ Z в направл. вектора l(Δ lZ). Δ lZ= f (M1)-f(M) это знач. не зависит от выбора сист. коорд.MM1=Δl-перемещ. точки в обл.,тогда средняя υ измен. скаляр. поля в указ. направл. определ Δ lZ/Δl. Если сущ. предел отнош. приращ. ф-ии в задан. направл.или к велич. перемещ. Δl при стремл. посл. к нулю, то этот предел назыв. произв. данной ф-ии в т.М по направл. вектора l, записыв:lim Δ lZ/ Δl=Z’l=dZ/dl при Δl→0,т.е. М1→М, так чтобы вектора ММ↑↑l Выберем сист. коорд. Перемещ. Δl может быть разлож. по направл. осей коорд. l(cosφ1,cosφ2).cosφ1= Δx/ Δl cosφ2= Δy/ Δl. Рассм. Δ Z в направл. Δl: Δ lZ= Z’x* Δx+ Z’y *Δy+α Δx+ β Δy. Δ lZ/Δl= Z’x* Δx/ Δl + Z’y *Δy /Δl +α Δx /Δl + β Δy/ Δl, Z’l=lim Δ lZ/Δl при Δl→0 из этого след. Δx→0,Δy→0, α→0, β →0. Z’l= Z’x* cosφ1+ Z’y* cosφ2, где φ1,φ2-дополн. друг друга до прям. угла. cosφ2=sin φ2 и поэт. Z’l= Z’x* cosφ+ Z’y* sin φ, φ-угол накл. l к Ох.
21. Производная по направл. для ф-ии U=f(x,y,z).Пусть в некотор. обл. прос-ва задано скаляр. поле с помощью ф-ии u= f(x,y,z) выберем в этой обл. некотор. т.М и зададим направл. с помощ. еденич. вектора l. Затем в обл. возьмем т.М1 так чтобы вектора ММ1↑↑l, из этого след. ф-ия при перех. от М к М1 получ. Δ lU= f (M1)-f(M), .MM1=Δl-перемещ. точки в обл.,тогда средняя υ измен. скаляр. поля при перех. М к М1 опред. след. образом Δ lU/Δl.Если сущ. предел отнош. приращ. ф-ии при перех. М к М1 к велич. перемещ. Δl, при Δl→0, так чтоб вектора ММ1↑↑l, то этот предел назыв. произв. ф-ии в т.М по напрвл. вект. l. lim Δ lU/ Δl=U’l=dU/dl при Δl→0, ММ1↑↑l . Определ. не зависит от выбор. сист. коорд. Выберем одну из них. Единич. вектор определ. напрвл. в обл. имеет коорд.l(cosφ1,cosφ2, cosφ3), где φ1,φ2,φ3-углы накл. l к осям сист. коорд. cosφ1= Δx/ Δl ,cosφ2= Δy/ Δl, cosφ3= Δz/ Δl . Δ lU= U’x* Δx+ U’y *Δy+U’z* Δz +α Δx+ β Δy+γ*Δz. Δ lU/Δl== U’x* Δx/Δl + U’y *Δy/Δl +U’z* Δz /Δl +α Δx/ Δl + β Δy/Δl +γ*Δz./Δl . Δ lU/Δl= U’x* cosφ1+ U’y * cosφ2 +U’z* cosφ3 +α *cosφ1+ β * cosφ2+γ* cosφ3, при Δl→0 из этого след. Δx→0,Δy→0, Δz →0,α→0, β →0,γ→0. U’l= U’x* cosφ1+ U’y* cosφ2+U’z* cosφ3.
22. Градиент Ф. z = f(x, у), его св-ва. Град-ом данной ф-ии в каждой т. Области наз-ся вектор коорд. кот. Явл. знач. частных производный ф-ии в этой т. Grad u(u`x; u`y; u`z) – вектор è Grad u =u`x*i +u`y*j +u`z*k (!i,j,k – векторы !); если в обласи простр. задано ск. поле диффиренцируемой ф-ии, то на этой же области опр-но векторное поле градиента. Аналогично выводиться град-нт для ф-ии 2-х переменных è Grad z =z`x*i +z`y*j 10 Скорость изменения скалярного поля в данной т. принимает max значение в направлении вектора градиента Док-во скорость изм. скал. поля -> δz/de = z`x*cosφ + z`y*cosφ(1) ; e(вектор)( cosφ; sinφ); grad(z`x; z`y). Заметим что произв. По направлению вектора предст. Собой скалярное про-ие векторов е и z. Скорость будет max если произведение по направл принимает max начение, то есть скал. произв вектор. прин max знач. a*b = |a|*|b|cos( a^b) => max скорость когда е сонаправлен с grad; покажем что в этом случае e` =|grad|è cosφ = z`x/|grad| и sinφ = z`y/|grad| подставим эти значения в (1) получим
δz/de = z`x/|grad| *cosφ + z`y/|grad| *cosφ = sqrt(z`2x+ z`2y)= |grad z| 20 Вектор град-та в любой т. области перпенд. к линии уровня проход. через эту точку, т.е. перп касательной к линии уровня в данной точке.; Пусть скал поле в нек-ой области на полс-ти XY задано ф-ей z=f(x,y). Выберем в обл т. М(x0, у0). Изсвестно что через эту т. проходит линия уровня. Соотв. уровень z=с можно определить из условия f(x0, у0)=c, тогда уравн линии уровня примет вид f(x,y)=c èпродиф-ем это ур-е -> z`x*dx + z`y*dy =0 ; grad z (z`x; z`y) ; dr(dx,dy) – касательная è в левой части скалярное произ-ие векторов grad и e, т.к оно = 0, то они перепендикулярны
23.Экстремум функции z = f(x, у),
Рассмотрим функцию 2х переменных z=f(x,y) в области D, пусть р0(x0,y0) - внутренняя точка этой области.
Опр. Точка р0 наз. Точкой max функции, если в некоторой окресности этой точки выполняется неравенство:
f(x,y)< f(x0,y0)
min - наоборот
Теорема: Необход. Усл. существования экстремума функции в точке р0.
Если ф-я z=f(x,y) диф-ма в точке р0 и имеет в этой точке экстремум, то часные производные функции в этой точке равны нулю.
f¢x(x0,y0)=0 f¢y(x0,y0)=0
Пусть в точке р0 функция достигает max. Рассмотрим часную производную этой функции по у. f¢y(x,y)=j¢(у)
При нахождении этой частной производной мы имеем дело с функцией, зависящей только от х, при этом эта функция в точке р0 достигает max, поэтому по теореме о существовании экстремума Ф. одной перемен. имеем: j¢( y0)=0 ® f¢y(x0,y0)=0, аналогично по х.
Опр. Точка р0 при этом наз. стационарной точкой (в которой часные производные равны нулю). Из этого следует, что экстремум функция 2х переменных может достигать только в стационарных точках (если она диф-ма ), но не во всякой стационарной точке функция достигает экстремума, т.к это только необходимое условие, но недостаточное условие.
Теорема: Достаточное условие существования экстремума ф-ции 2х переменных.
Пусть ф-я z=f(x,y) диф-ма в точке р0 и эта точка явл. стационарной точкой , найдем часные производные 2ого порядка этой функции r=¶2z/¶x2 s=¶2z/¶x¶y t=¶2z/¶y2
Вычислим в точке р0 значение выражения (rt-s2)po, если это выражение >0, то в т. р0 сущ. экстремум.
При этом если r>0 р0 -min; r<0 р0 -max
Если rt-s2<0 - экстремума нет.
rt-s2=0 - экстремум возможен, требуются дополнительные исследования.
24. Условный экстремум Ф. z = f(x, у). МетодЛагранжа.
Пусть дана z=f(x,y). Перемен. х и у связ нектр усл. φ(х,у)=0. Это ур-ие называется ур-ем связи. Треб найти экстремум данной Ф при условии. Указ в уравн. связи. Экстр Ф z=f(x,y) при усл φ(х,у)=0 наз знач Ф в такой т(х0у0), для ктр сущ окрест-ь(о-ь) в виде множ-а х,у что (S от х,у до х0,у0)<ε. Для всех точек этой о-и связ услов φ(х,у)=0 выпол нерав f(x,y)<=f(x0,y0)- усл макс или f(x,y)>=f(x0,y0)- услов мин Точка (х0,у0) наз усл мин или макс, если она удовлет. Усл. f(x0,y0)=0, и для нее сущ окр-сть точки (х0,у0), что для люб точки (х,у) этой окр-и удов условию f(x,y)=0 выпол нерав f(x,y)>=f(x0,y0) или f(x,y)<=f(x0,y0).
Метод Лагранжа. Пусть дана Ф z=f(x,y) и ур-ии связи φ(x,y)=0; Нужно найти Экстр. данной Ф при зад. условии. Для решения зад рассмотр вспом Ф от 3-х переменных (х,у,λ). Ктр наз Ф Лагранжа. => L(x,y,λ)=f(x,y)+λφ(x,y). Сост вспом Ф: необход услов для усл Экс сформул в теореме: если (х0,у0) явл усл Экс Ф z=а(чбн) при услов φ(x,y)=0, то сущ λ0 такие что (x0,y0,λ0) явл т. обл. Экс. L(x,y,λ). Это означает неод условием явл рав-во=0 всех ч-х производ f-u Лагранжа. L’x=0; L’y=0;L’λ=0; L(x,y,λ), т.е. L(x,y,λ)=f(x,y)+λφ(x,y); Все в системе: L’x=0; f’(x,y)+λφ’x(x,y)=0; L’y=0; f’y(x,y)+λφ’y(x,y)=0; L’λ=0; φ(x,y)=0;. Из получ сист опред крит точки. Посл ур-е представл собой ур-е связ. Из 1-х двух следует, что вектор град Ф φ(x,y) и f(x,y) явл коллинеарн век-и, т.к. по определ. grad φ(x,y)=(φ’x,φ’y);
grad f(x,y)=(f ’x,f ’y); grad f(x,y)=-λ*grad φ(x,y).
26.Метод наим. квадр. при нахожд. эмпирич. фор-л (y=ax2+bх+с). Нахожд. эмпирич. фор-л обычно связано с каким-нибудь экспер., в ходе эксперим. по значению одной из перм-oй определ. знач. другой перм-ой и по набору этих знач. отыскивается формула наиболее точно, удовлетв. этим значениям. Опис. ф-лы идет по плану:1)по результатам эксперим. составл. таблицу значений; 2)на корд-ой пл-ти наносится точки по координатам (xi,yi) и по их знач. Выбир. график какой-нибудь ф-ии наиболее близко располож. к этим точкам; 3) находятся пар-ы, т. е. коэфф. соотв. ур-ия. Найденная таким образом ф-ла носит назв. эмпирической ф-ой. Нахожд. Пар-ов подобр. ф-ии может быть выполнен методом наим. квадратов. Суть,которого состоит в следующ: пусть ф-ия имеет вид y=f(x), для каждого xi наход. знач. этой ф-ии, т. е. f(x1), f(x2). Парам-ры этой ф-ии должны удовл. условию, чтобы они минимально отлич. от знач. yi, получ. в ходе эксперим., т.е. чтобы yi-f(xi)=min. Надо, чтобы сумма их квадратов принимала миним. знач. (f(x1)-у)2+(f(x2)-у)2+…+(f(xn)-уn)2=min. Рассм. второй случ: если искомая ф-ия y=ax2+bх+с. Найти a,b,c. S(a,b,c)= Σni=1((axi2+bxi+c)-yi)2=min. dS/da=0, dS/db=0, dS/dc=0, dS/da= Σni=12(axi2+bxi+c-yi)*xi2=0, dS/db= Σni=12(axi2+bxi+c-yi)*xi=0, dS/dc=Σni=12(axi2+bxi+c-yi)*1=0. Получаем систему состоящую из a* Σni=1xi4+b Σni=1xi3+сΣni=1xi2=Σni=1xi2yi и a* Σni=1xi3+b Σni=1xi2+сΣni=1xi=Σni=1xiyi и a* Σni=1xi2+b Σni=1x+с*т =Σni=1yi. Составим таблицу сост. из:xi,yi,xi2,xi3,xi4. Найдя коэфф. системы и решив её получаем искомую эмпирическую ф-ию.
27.Введение двойного интеграла и его геометрич. смысл. Пусть дана непрерывн. ф-ия Z=f(x,y) на замкнутой области D, область назыв замкнутой, если ко мн-ву всех её внутр. точек присоед. точки границы. Разобьём область D произвольн. образом на конечное число ячеек. f(Pi)*ΔSi рассм. сумму всех таких произвед. Σni=1 f(Pi)*ΔSi=Vn – такая сумма назыв. интегральной суммой для ф-ии Z=f(x,y). Кажд. слагаем. в этой сумме представляет собой объем призматического тела с основан-ем Δxi большие ребра ║ оси Z хотя бы одна точка поверх-ти лежит на кажд. ступеньки верхней части тела, при условии,что для любой точки Pi, f(Pi)≥0.Определ:если сущ. предел посл-ти указ. интегр-ых сумм V1,V2,…,Vn, при n→∞ и max ΔSi→0, то этот предел назыв. двойным интегр-ом по обл. D от ф-ии f(x,y),т.е.limVn=limΣni=1f(xi,yi)*ΔSi=∫D f(x,y)dS при n→∞, max ΔSi→0. Сущ. теорема,если ф-ия Z=f(x,y) непрерывн. на замкн. обл. D, то предел интегр-ых сумм сущ. и не зависит от способа разбиения обл. D на ячейки и выбора точ. Pi в кажд. такой ячейки. На основе этой теор. обл. D можно разбить на ячейки прамыми║осям сист. корд. Si=Δxi* Δyi, dS=dx*dy; ∫∫Df(x,y)dS=∫∫Df(x,y)dxdy.Геом. смысл:если f(х,у)≥0 на всей обл. D, то знач. указ. двойного инт-ла есть V цилиндрич. Тела основан. котор. служит обл. D,образующ. котор., проходит через каждую т. границы обл. ║оси Z, и котор. сверху огранич. поверхн. определ. ф-ей Z=f(x,y).
28.Св-ва двойн. интеграла, его оценка.
1постоян. множитель поинтегр. ф-ии можно выносить за знак интеграла 20 Двойной интеграл от сумм непрер. ф-ии по области равен сумме таких же интегралов от каждого слагаемого ∫∫D((f1(x,y)+f2(x,y))dxdy; ∫∫Df1(x,y)dxdy+∫∫Df2(x,y)dxdy 30 Если область D разбила на 3 или кон. Число частей, то 2-ой интеграл от данной ф-ии по области D = сумме двойных интегралов от этой ф-ии по всем областям составл. D: ∫∫D=D1+D2f(x,y)ds =∫∫D1f(x,y)ds+∫∫D2f(x,y)ds Оценка двойного интеграла: т.к. ф f(x,y) непрерывна на D, то она на ней max и min à M –max f(x,y) на D, m – min f(x,y) на D } è m*S(D)<= ∫∫Df(x,y)ds<= max S(D)
29.Понятие правильной области. Вычисление двойного интеграла. Область на пл. ОХ наз-ся правильной в направл. оси ОХ если любая прямая проход. через внутреннюю точку области, пересек. ее границу точно в двух т. область на коорд пл. ОХУ наз-ся правильной в направл. Оу если любая прям. Проходит через внутр т. области || оси Ох, пересекают ее гран. в 2-х точках. Область наз-ся правильной если она правильна одновременно прав-на обеих осей
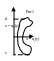
Пусть D правильна в напр. Ох – в этом случае область огран-на у=с, у=d, x = φ1(y), x = φ2(y) В этом случае все сводиться к вычисл. Кратного интервала след. Вида - ∫∫Df(x,y)dxdy=∫CD dy ∫ φ1(y) φ2(y) f(x,y)dx (рис1)
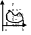
Пусть D правильна в напр. Оу – в этом случае область огран-на отрезком от а до b, x = φ1(y), x = φ2(y) ) 3)
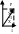
Пусть D-прав. в отнош обеих осей тогда поядок итегрирования может быть выбран любой, наиболее удобным случаем. Область огран-на у=х, у=0, х=1
Если область не явл. Правильной не в напр. ОХ не в напр. ОУ то для нахожд 2-го интреграла данную область разбивают на части и высчитывают сумму интегралов(либо вычитанием одного интеграла из другого(рис4))
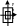
30.Применение дв-го интеграла при вычисл. площадей и объемов.Двойн-ой интег-ал примен. при вычисл. V цилиндрич. тел, основан. каждого из котор. явл. замкнут. обл. D в пл-ти Оху, образующ. котор. парал-ые оси Z. Сверху это тело огранич. поверхн. задан.ф-ей Z=f(x,y), где f(x,y)≥0 на всей обл.D. Замеч: с помощ. двойн. интеграла можно вычисл. V геометрич. тела, котор. проектир. в некотор. замкнут. обл. D в пл-ти ху.
Вычисл. можно следующ. образом: V дан. тела представл. собой разность V двух цилиндрич. тел, с одним и те же основ. и образующ, но 1-ое тело покрыт. сверху поверхн. Z=φ2(x,y) и снизу Z= φ1(x,y), V=∫∫D φ2(x,y)- ∫∫D φ1(x,y)dxdy. Нахожд. площ. замкнут. обл. в пл-ти ху.
Если через каждую т. границы обл. провести образующ.║ осиZ на высоту равн. 1, то получ. цилиндрич. тело в основ. котор. лежит обл. D и h=1, тогда V=Sосн.*h=S(D)*1, площ. осн. числен. равна объему указ. цилиндра. Ур-ие поверхн. огранич. цилиндр сверху имеет вид Z=1, т.е.f(x,y)=1. S(D)=V=∫∫D1dxdy. Нахожд. площ. обл. на поверхн. задан. ур-ем Z=f(x,y), ели эту обл. обознач. δ, а ее проекцию в пл-ть ху через D, тогда δ =∫∫Dsqrt(1+Z’2x+Z’2y)dxdy. Определ. площ. части поверхн. цилиндра задан. ур-ем y2+z2=a2,котор. вырез-ся др. цилиндром x2+y2=a2
На чертеж. заштрих. 1/8 часть поверхн. котор. второй цилиндр высекает на первом.1/8 часть,т.к. 3 коорд. Пл-ти разрезают простр-во на 8 частей и кажд. из этих частей входит такой кусоч. поверхн. 1/8δ=∫∫Dsqrt(1+Z’2x+Z’2y)dxdy. Z=sqrt(a2-y2), Z’x=0, Z’y=-2y/(2*sqrt(a2-y2)), 1+ Z’2x+Z’2y=a2/(a2-y2) ; 1/8δ=∫∫D a/sqrt(a2-y2)dxdy=∫a0dy∫sqrt(a*a)0 a/sqrt(a2-y2)dx=∫a0ady=a2; δ=8a2.
