32. Моменты инерции сечения.

Геометрической хар-ой, учитывающей площадь сечения, его форму и расположение фигуры относительно оси явл. момент инерции. Различают: осевые, полярные и уентробежные моменты инерции сечения.(рис) Осевой момент инерции относительно какой-л. оси – произведение элементарных площадок на квадрат расстояния до данной оси. ( ) Полярный момент инерции относительно какой-л. т0 – сумма произведений элементарных площадок на квадрат расстояния до этой т. Полярный момент инерции –сумме осевых моментов ин. Центробежный момент инерции:

33. Особенности центробежного момента инерции. Моменты инерции сложного сечения.

Центробежный момент инерции: Осевой и полярный момент инерции всегда положительны, центробежный может быть отриц, полож, и =0. При повороте осей центробежный момент инерции меняет знак. (рис) Возьмем симметричную фигуру относительно оси y (рис) Если сечение имеет оси симметрии, то центробежный момент инерции относительно этой оси и ей =0. При вычислении моментов инерции сложного сечения относительно како-л. оси его разбивают на простые фигуры. Для каждой нах момент инерции относительно заданной оси. Момент инерции всего сеч. = сумме моментов инерции составных частей.

34. Зависимости между моментами инерции относительно осей.

Имеем сеч. площадью А. Через цент тяжести проведем центральные оси (рис) Определим осевые моменты инерции относительно осей X1 и У1, которые проведены || центральным и отстоят от них на расстояние а и в. . , Теорема: момент инерции относительно любой оси ||-й центральной = моменту инерции относительно центральной оси + произведение площади на квадрат расстояния между осями.

Найдем центробежный момент инерции относительно осей y1 и x1: : , . Центробежный момент инерции относительно осей ||-х центральным = центробежному моменту инерции относительно центр-х осей + произведение площади на расстояние между осями.

35. Моменты инерции сечений простой формы.(рис)

1. Прямоугольник. Выч. момент инерции относительно осей Х, проход. через центр тяжести сеч., || основанию. . , dA=в dy, где dA- площадь слоя ,

2. Равнобедренный треугольник. Выч. момент инерции относительно осей Х, проход. через основание треугольника. dA= , Найдем момент инерции относительно проходящей через центр тяж-ти треугольника, используя ф-лу перехода к ||-м осям. , , = , =

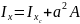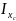3. Прямоугольный треугольник. = , =

4.Круг. На расстоянии от центра тяжести круга выделим элементарную полосу толщиной d и найдем полярный момент инерции относительно центра круга. , ,

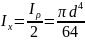
5. Полукруг.

36.зависимость между моментами инерции при повороте осей. Предположим для некоторой площади известны осевые моменты инерции относительно осей х и у. рис. . Найдем моменты инерции относительно осей , которые повернуты на угол α против часовой стрелки относительно заданных осей. ; ; ; . Сложим . Сумма моментов инерции относительно 2ух взаимно перпендикулярных осей величина постоянная

37. Главные оси и их положения. Сумма моментов инерции относительно любых взаимно перпендикулярн. осей не меняется при их повороте ⇒ при повороте осей изменяют свою величину , причем один из них увеличивается, а другой уменьшается. Всегда можно определить такое положение осей , при котором моменты инерции будут иметь экстремальное значение (один max, другой min). Для определения такого положения осей возьмем производную от по углу . . Сравним выражения. . ⇒центробежный момент инерции относительно главной оси. Найдем угол : . Если полученное значение положительное, то для отыскания главной max оси необходимо отложить его против часовой стрелки от оси с большим моментом инерции. Перпендикулярная ей ось будет главной min осью, т.е. относительно которой момент инерции принимает min значение. Т.о. главные оси – оси, относительно которых центробежный момент инерции =0, а осевые моменты инерции принимают экстремальное значение.

38. Главные моменты инерции. Моменты инерции относительно главных осей наз. главные моменты инерции. Через любую точку сечения можно провести главные оси по сопротивлению материалов наивысший интерес представляют главные оси, проходящие через центр тяжести сечения, такие оси наз. главными центральными, а моменты инерции относительно этих осей наз. главными центральными. Главные оси обозначаются . А главные моменты инерции ; . Главные моменты инерции определяются по формулам: . В этой формуле ставится + если считается и -, если . Для симметричных осей можно сразу провести главные центральные оси. Одна главная ось совпадает с осью симметрии, вторая ей перпендикулярна и проходит через центр тяжести сечения. Если есть 2 оси симметрии, то они являются главными центральными. Рис. . Рис. т.к - ось симметрии. Рис. . Если сечение имеет более 2ух осей симметрии(круг, кольцо, равносторонний треугольник), то все они являются главными центральными осями и моменты инерции относительно этих осей равны между собой.

39. Круг инерции(мора). Определение моментов инерции можно производить при помощи круга инерции. Предположим, имеем сечение для которого необходимо определить главные центральные моменты инерции и положение главных осей, т.е. угол α. Рис. Моменты инерции относительно проходящих через центр тяжести известны, причем ; . Построим круг инерции. Рис. 1) в осях откладываем моменты инерции . В точке восстанавливаем перпендикуляр и откладываем = центробежному моменту инерции. В точке проводим перпендикуляр и откладываем отрезок . Соединяем точки и и находим центр точку С. Радиусом = проводим окружность. Находим точки пересечения окружности с осью х: 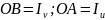. находим полюс P. Для этого проведем через точку 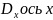. вторая точка пересечения проведенной оси х и окружности будет полюсом круга Р. Проводим прямые РА, РВ. РА соответствует оси U, РВ – оси . Угол между проведенной осью х и осью U будет исконным углом α. Из круга мора можно вывести: .

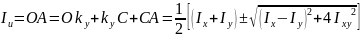40. понятие о радиусе инерции. Предположим имеем сечение – прямоугольник. Момент инерции относительно оси Х известен. Рис. . В этом случае величина y является переменной. Найдем значение , при котором величина для заданного сечения не изменяется. ; ; ; 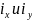- радиусы инерции(см). Если известны главные моменты инерции, то тогда определяется главные радиусы инерции. ;

41. кручение. Определение. Внутренние силы и их эпюры. Кручение – такой вид деформации элементы конструкции, когда в поперечном сечении его возникает только одна внутренняя сила – крутящий момент . Внутренние силы: для определения крутящего момента используют метод сечений. Сделаем сечение за вторым моментом. Правую часть отбросим. В сечении будет возникать крутящий момент . Рис. . крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов расположенных по одну сторону от сечения. Примем след.правила знаков: если смотреть со стороны сечения и внешний момент вращает отсеченную часть по часовой стрелке, то крутящий момент в сечении будет положительным. Предположим, имеем вал, на котором находится ряд шестерней с различными скручивающими моментами. Рис. . Намечаем участки бруса. Границами участков являются точки действия внешних моментов. По эпюре крутящего момента нельзя судить о прочности стержня. Необходимо найти напряжение.

42. Напряжение при кручении. Проведем опыт: на поверхности вала нанесем ряд параллельных, продольных и поперечных линий. В результате деформации: 1) все образующие повернулись на угол , произошел сдвиг ⇒ возникают касательные напряжения. 2) поперечные линии не сдвигались, и не изменилось расстояние между ними ⇒ нормальное напряжение вдоль продольной оси отсутствует. 3)радиус в торце вала остались прямым, но повернулись на угол . На основании опыта делаем вывод, что гипотеза плоских сечений при кручении выполняется, т.е. плоские поперечные сечения до деформации остаются плоскими и последе формации. При кручении в поперечном сечении вала возникает касательное напряжение. Предположим имеем элементарный участок скручиваемого вала длиной dz. Рис. Под действием момента m сечение поворачивается на . Образующая АВ сдвигается в положение . . Поскольку произошел сдвиг, используем закон Гука при сдвиге . Эта зависимость для наружного слоя вала. В любой точке на расстоянии ρ от центра вала напряжения будут равны. . В сечении выделим элементарную площадку dA на расстоянии ρ от центра круга. Тогда - элементарная внутренняя сила. Рис. - элементарный внутренний момент по площадке dA. Тогда . Подставим из первого выражения. ; - полярный момент инерции. 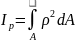; . Подставляем полученное выражение и получаем - формула для определения касательного напряжения в любой точке поперечного сечения вала. - расстояние от центра вала до исследуемой точки.

43. полярный момент сопротивления. Расчет на прочность при кручении. Из формулы видно, что ⇒ ⇒ Эпюра касательных напряжений имеет в поперечном сечении вид. Рис. Выражение для определения - полярный момент сопротивления – это отношение полярного момента инерции к расстоянию от центра до наиболее удаленной точки сечения. Характеризует прочность при кручении. Определим для некоторых сечений. Рис. - для сплошного круглого сечения. Рис. 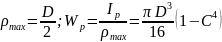; – для трубчатого сечения. Определить можно проверив прочность элементов работающих на кручение. Условие прочности: . - расчетное сопротивление на срез.

58. рациональные формы сечения балок. При изгибе форма сечения играет существенную роль. Поскольку прочность балки характеризуется моментом сопротивления, зависящего как от размеров сечения, так и от очертания сечения. Подбирая сечение надо стремиться чтобы при min его площади, а ⇒и наименьшей затрате материала, получить наибольший момент сопротивления. Для этого следует большую часть площади поперечного сечения расположить как можно дальше от нейтральной оси. Рассм. 2 сечения одинаковой площади. Рис. Т.к. площадь в сечении одинакова, то наиболее рациональным будет сечение, у которого момент сопротивления больше. Т.к. h и одинаковы у этих сечений, то момент сопротивления будет больше у сечения, у которого больше момент инерции . У двутаврового сечения будет больше, т.к.значительная часть его площади наиболее удалена от нейтральной оси. Двутавр самая рациональная форма поперечного сечения балки. Самая нерациональная – круглая. Рис. Т.к. основная масса материала находится на нейтральной оси. Для балок из хрупкого материала (чугун) рациональным является сечение не симметричное относительно нейтральной оси. Хрупкий материал лучше работает на сжатие или растяжение , поэтому целесообразно расположить сечение так, чтобы наибольшее растягивающее растяжение балки были значительно меньше наибольших сжимающих. Рис. Сечение 2 является рациональным, т.к. растягивающее напряжение меньше сжимающих.

59. понятие о балках переменного сечения. В ряде случаев необходимо изготавливать балки переменного сечения. Рис. Нормальное и касательное напряжение балки переменного сечения определяется по формулам . Однако при расчете следует, что в местах изменения площади сечения напряжение изменяется, в точках перехода будут max напряжение, которое учитывается коэффициентом концентрации. ; теоретический коэффициент концентрации, определяемый методом теории упругости. Для уменьшения концентрации напряжений необходимо устранить резкие изменения контура продольного сечения балки, применяя плавные переходы. Рис. Рассм. растяжение. Рис. , где - наименьшее среднее напряжение по ослабленному сечению. – площадь сечения ослабленное отверстием.

60. понятие о балках равного сопротивления. В балках постоянного поперечного сечения, которое рассчитано по наибольшему изгибательному моменту материал используется не рационально. Только в сечении с наибольшим изгибающим моментом возникает допускаемое напряжение, в остальных сечениях материал загружен не достаточно. К балкам равного сопротивления относятся балки у которых max напряжение во всех сечениях по длине одинаково. . Рассмотрим балку с постоянной высотой h. Необходимо найти ширину, при которой max напряжения будут одинаковы . Рис. .наибольший изгибательный момент, возникающий в опоре, будет равен . Изгибат. момент в сечении z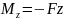 . Моменты сопротивления соответственно: 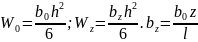– ширина сечения. Min ширина сечения определяется из условия прочности касательного напряжения. .

61. понятие о центре изгиба. Рассм. распределение касательных напряжений в поперечном сечении балки тонкостенного профиля (швеллера) испытывающего поперечный изгиб. Рис. В стенке возникает касательное напряжение , которое определяется по формуле Журавского. В полках возникает , которое определяется тем же путем. Найдем статические моменты отсеченной площади. . Эпюра имеет вид треугольника. Рис. -равнодействующая касательных сил возникающих в полках; – в стенке. Можно принять, что в рассматриваемом сечении . ; . Под центром изгиба понимают такую точку при приложении нагрузки к которой будет происходить кручение. Для устранения кручения к швеллеру приваривают угловой коротыш, куда и прикладывают нагрузку.

64. напряжение в наклонных сечениях при линейном напряженном состоянии (ЛНС). При растяжении, сжатии бруса все точки тела находятся в состоянии ЛНС. Найдем нормальное касательное напряжение в наклонной площадке растянутого стержня. Рис. Напряжение в поперечном сечении определяется по формуле Далее докажем, что напряжение, действующее в поперечном сечении, является главным. Пусть нормаль к наклонной площадке n составляет с угол α. В наклонной площадке будут возникать нормальные напряжения и . Их мы определим рассматривая статическое равновесие нижней части стержня. Рис. . Для определения силы, действующей на площадку, необходимо напряжение умножить на площадь площадки, на которую она действует. ; ⇒ ; . Проанализируем полученные формулы: . Из этого анализа запишем выводы: 1)площадки, на которых отсутствуют касательные напряжения, называются главными, т.е. поперечное м продольное сечение являются главными площадками ⇒ нормальное напряжение, действующее в поперечном сечении является главным. 2) максимальное напряжение при растяжении, сжатии возникает в сечениях под углом 45˚ к поперечному сечению и равно половине главного напряжения. Это подтверждается опытом: при сжатии чугунного образца он разрушается под углом 45˚ к продольной оси, т.к. чугун хуже сопротивляется сдвигу чем сжатию.