
- •Программа сортировки по индексам
- •Способ 5
- •1) Критерий хи - квадрат (Пирсона)
- •2) Критерий Романовского
- •3) Критерий Колмогорова
- •Ринунок 2.13 – Эмпирическая (1) и теоретическая (2) функции распределения
- •4) Критерий Мизеса-Смирнова
- •2) Статистическое имитационное моделирование
- •1) Критерий хи - квадрат (Пирсона)
- •2) Критерий Романовского
- •3) Критерий Колмогорова
- •Ринунок 2.13 – Эмпирическая (1) и теоретическая (2) функции распределения
- •4) Критерий Мизеса-Смирнова
- •2) Статистическое имитационное моделирование
- •1) Критерий хи - квадрат (Пирсона)
- •2) Критерий Романовского
- •3) Критерий Колмогорова
- •Ринунок 2.13 – Эмпирическая (1) и теоретическая (2) функции распределения
- •4) Критерий Мизеса-Смирнова
- •2) Статистическое имитационное моделирование
- •3.6. Транспортная задача линейного программирования
- •3.1. Безусловная оптимизация для одномерной унимодальной целевой функции
- •100. Одномерная задача динамического программирования.
- •104.Расчёт выигрышей при маршрутизации перевозок мелких партий ресурсов по методу Кларка-Райта
- •3.10.2. Задача о назначениях
3) Критерий Колмогорова
Статистика критерия Колмогорова определяется максимальным отклонением по границам интервалов между теоретической F(Хj) и эмпирической Fэ(Хj) функциями распределения (рисунок 2.13).
1.0 1
F(x),Fэ(x)
0.60
2
0.20
Xmin Xmax x
X0 X1 X2 X3 X4 Xj (j=N=5)
Ринунок 2.13 – Эмпирическая (1) и теоретическая (2) функции распределения
Для этого для каждого значения Хj вычисляется модуль разности между эмпирической и теоретической функциями распределения abs(F (Хj)- Fэ (Хj)) и затем из всех рассчитанных значений находится максимальная величина
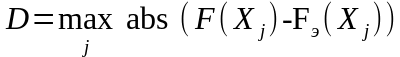 .
.
Вычисляется значение статистики критерия Колмогорова
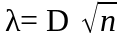 .
.
Полученное значение статистики необходимо сравнить с табличным. При принятых значениях уровня значимости (0.1–0.2) по таблице определяют критическое значение и проверяют условие
< .
При выполнении условия гипотеза о распределении случайной величины по предполагаемому теоретическому закону по критерию Колмогорова может быть принята, в противном случае – отклонена. При больших значениях требования к согласованности распределений повышаются.
Табличные значения критерия Колмогорова следующие:
Уровень значимости |
0.40 |
0.30 |
0.20 |
0.10 |
0.05 |
Значение критерия |
0.89 |
0.97 |
1.07 |
1.22 |
1.36 |
4) Критерий Мизеса-Смирнова
Критерий Мизеса-Смирнова в отличие от критерия Колмогорова, который основывается на максимуме абсолютной величины разности между эмпирической и теоретической функциями распределения, использует статистику в виде суммы взвешенных через весовую функцию квадратов разностей между эмпирической и теоретической функциями по всем наблюдаемым значениям случайной величины
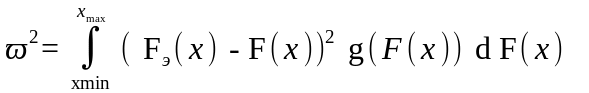 ,
,
где F(x) – теоретическая функция распределения;
Fэ(x) – эмпирическая функция распределения;
g(F(x)) – весовая функция.
Обычно используют весовые функции двух видов: g(F(x))=1, при которой все значения функции распределения обладают одинаковым весом, и
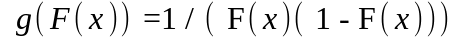 ,
при которой увеличивается вес наблюдений
на концах распределения.
,
при которой увеличивается вес наблюдений
на концах распределения.
Ниже рассматривается критерий при весовой функции второго вида.
После выполнения интегрирования выражение для расчета статистики критерия имеет вид ,
где xi – результаты наблюдений, отсортированные по величине (x i x i +1).
Полученное значение статистики ω2 сравнивается с табличным значением ω2. Значение принимается на уровне 0.1– 0.2. Табличное значение критерия при =0.1 составляет ω2 =1.94 и при =0.2 – ω2 =1.42. Если рассчитанное значение статистики больше табличного, то гипотеза о согласованности отвергается, и если нет – то принимается.
Компьютерная программа для исследования распределения случайных величин приведена в приложении 2. Состоит из головной программы и модулей для исследования распределения непрерывных и дискретных величин.
49.Корреляционно-регрессионный анализ. Нахождение коэффициентов уравнения регрессии
Изучение статистических зависимостей основывается на корреляционно-регрессионном анализе. Корреляционный анализ позволяет ответить на вопрос о существовании зависимости между случайными величинами, а также оценить степень тесноты статистической зависимости. Инструментом регрессионного анализа является уравнение регрессии. Исходными данными для проведения корреляционно-регрессионного анализа является статистическая информация, содержащая значения факторов и зависимого от них параметра.
Одной из возможных схем проведения корреляционно-регрессионного анализа является следующая:
1) проводится взаимный парный корреляционный анализ между всеми возможными сочетаниями факторов и при существенности связи между факторами пары один из дублирующих друг друга факторов (зависимый фактор) исключается из дальнейших расчетов;
2) принимается вид уравнения регрессии (модели связи);
3) рассчитываются параметры уравнения регрессии;
4) проверяется значимость отдельных факторов в модели и адекватность уравнения регрессии экспериментальным данным в целом. Если нет малозначимых факторов и уравнение регрессии согласуется с экспериментальными данными – исследование закончено, а иначе на п.5;
5) при наличии малозначимых факторов они исключаются из расчетов и переход на п. 3 и при неадекватности уравнения регрессии экспериментальным данным переход на п. 2 для принятия нового вида уравнения регрессии.
Если связь оказалась несущественной для различных видов уравнения регрессии, то необходимо считать, что зависимая переменная не зависит от учитываемых факторов.
Полученное уравнение регрессии является моделью связи между факторным пространством и зависимой переменной (параметром).
Статистикой, характеризующей тесноту связи между факторами и зависимой переменной, является коэффициент множественной корреляции.
Коэффициент множественной корреляции показывает, какая часть дисперсии зависимой переменной объясняется полученным уравнением регрессии
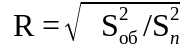 ,
,
где
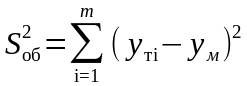 –
объясненная сумма квадратов отклонений
от оценки математического ожидания;
–
объясненная сумма квадратов отклонений
от оценки математического ожидания;
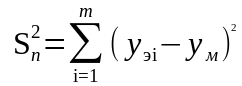 –
полная
сумма квадратов отклонений от оценки
математического ожидания;
–
полная
сумма квадратов отклонений от оценки
математического ожидания;
yм – оценка математического ожидания случайной величины.
Разность между полной и объясненной суммой квадратов является остаточной (необъясненной) суммой отклонений от оценки математического ожидания
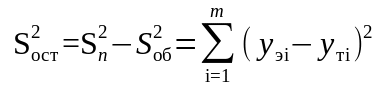 .
.
Тогда
через
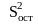 значение коэффициента множественной
корреляции рассчитывается по формуле
значение коэффициента множественной
корреляции рассчитывается по формуле
 .
.
Значения R может быть в пределах от 0 до 1.0. При R = 0 связь между факторами и зависимой переменной отсутствует, а R = 1.0 указывает на функциональную зависимость.
Значимость факторов оценивается по критерию Стьюдента.
Статистика критерия Стьюдента tj рассчитывается по формуле
tj = abs(aj / saj),
где bj – значение j-го параметра (коэффициента) в уравнении регрессии;
s bj – среднеквадратическое отклонение параметра bj .
Если расчетное значение статистики критерия Стьюдента tj для выборочного параметра (коэффициента) при рассматриваемом факторе больше табличного значения критерия tт γ,k, то считается, что нет оснований считать данный фактор малозначимым. Табличное значение tтγ,k определяется заданной доверительной вероятностью γ и числом степеней свободы k. Число степеней свободы определяется по выражению
k = m - n - 1,
где m – число эмпирических точек, в которых определен зависимый параметр; n – число факторов, входящих в уравнение регрессии.
Доверительный уровень значимости рекомендуется принимать равным 0.01–0.1 (чем меньше γ, тем выше требования к значимости фактора).
Для проверки существенности коэффициента множественной корреляции и таким образом оценивания согласованности уравнения регрессии с экспериментальными данными используется статистика критерия Фишера
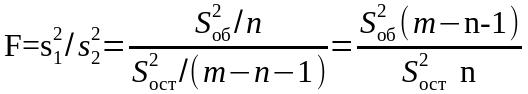 или
или
,
где
и
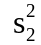 –
соответственно объясненная и остаточная
дисперсия для зависимого параметра.
–
соответственно объясненная и остаточная
дисперсия для зависимого параметра.
Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > Fт). Табличное значение Fт определяется в зависимости от уровня значимости γ и числа степеней свободы k1 и k2 :
k1 = n ;
k2= m - n- 1 .
Уровень значимости (вероятность) рекомендуется принимать 0.01 – 0.05 (чем меньше, тем жестче требования к адекватности модели).
Если F<Fт, то считается, что уравнение регрессии не согласуется с экспериментальными данными.
Статистику критерия Фишера можно использовать для оценки значимости отдельных факторов. Фактор следует считать малозначимым в том случае, если его исключение из модели не вызывает существенного снижения статистики критерия Фишера. При этом исключение малозначимого фактора может обеспечить увеличение статистики F . Например, если при m=7 и n=3 имели =2.1, а =0.7, а при исключении одного из факторов (n=2) получили =1.8 и =1.0, то
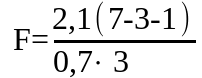 =3.0
при n=3;
=3.0
при n=3;
=3,6 при n=2.
Увеличение статистики F в приведенном примере указывает на малозначимость исключаемого из модели фактора.
Мерой согласованности уравнения регрессии с экспериментальными данными может служить также коэффициент средней линейной ошибки аппроксимации E
.
Компьютерная программа проведения множественного корреляционно-регресионного анализа приведена в приложении 4.
50.Имитационное моделирование СМО (разомкнутая многоканальная система).
Многоканальная разомкнутая система массового обслуживания
В качестве примера рассматривается многоканальная СМО с простейшим потоком требований и экспоненциальным распределением времени их обслуживания (рисунок 2.16). Система с ожиданием и без приоритетов требований и каналов друг перед другом.
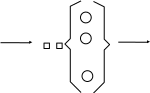
Каналы
1
Очередь 2
Входящий ... Выходящий
поток поток
n
Рисунок 2.16 – Схема многоканальной разомкнутой системы массового обслуживания
Поток требований на обслуживание характеризуется средней интенсивностью L (с-1, мин-1, ч-1 , сут-1) и имеет пуассоновский закон распределения. Доказано, что в этом случае интервалы между поступлениями требований распределены по экспоненциальному закону распределения. Длительность времени обслуживания требования характеризуется средней величиной tобс (потоком обслуживания v=1/tобс). Число каналов в системе – n.
Основные показатели функционирования многоканальной разомкнутой системы массового обслуживания рассчитываются по формулам:
вероятность того, что все каналы обслуживания свободны
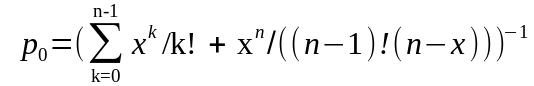 ,
,
где x = L tобс – приведенный поток, физическая сущность которого – число каналов, необходимое для обслуживания требований при детерминированных их потоке и времени обслуживания. Должно соблюдаться условие x < n ;
вероятность того, что в системе находится ровно k требований
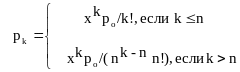
вероятность того, что все каналы заняты
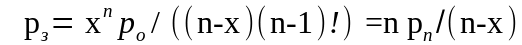 ;
;
вероятность того, что занято ровно n каналов
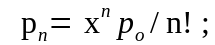
вероятность того, что время ожидания требованием начала обслуживания toж меньше или больше tз
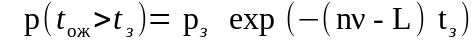 или
или
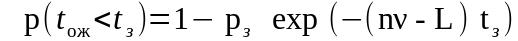 ;
;
среднее число незанятых каналов обслуживания
 ;
;
среднее число требований, простаивающих в очереди на обслуживание
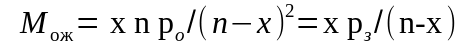 ;
;
среднее число требований на обслуживании
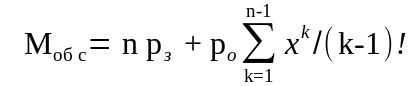 ;
;
средняя
длительность времени ожидания требованиями
начала обслуживания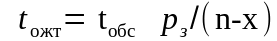 .
.
