7.8.Частица в одномерной бесконечно глубокой потенциальной яме. Волновые функции и квантование энергии.

Квантование энергии. Учтем, что физический смысл имеют лишь такие решения уравнения (тут и далее говорится про стационарное), когда невременная волновая функция и ее первые производные по координатам удовлетворяют стандартным условиям. Эти условия являются требованиями, накладываемыми на искомое решение дифференциального уравнения. Решения уравнения Шрёдингера, удовлетворяющие этим условиям, оказываются возможными лишь при некоторых значениях энергии Е, называемых собственными значениями энергии. Функции 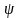, являющиеся решениями уравнения при этих значениях энергии, называются собственными функциями, принадлежащими собственным значениям Е.

Собственные значения Е могут образовывать как непрерывный, так и дискретный ряд. В первом случае говорят о непрерывном (сплошном) спектре энергии, во втором – о ее дискретном спектре.

Уравнение Шрёдингера является математическим выражением корпускулярно-волнового дуализма. Оно удовлетворяет принципу соответствия Бора и в предельном случае, когда длина волны де Бройля значительно меньше размеров, характерных для рассматриваемого движения, позволяет описать движение частиц по законам классической механики.

Для описания состояния квантовой системы в данный момент времени вводится комплексная волновая функция (пси-функция) . Она определяется так, что вероятность dP нахождения частицы в некоторый момент времени в элементе объема dV прямо пропорциональна и элементу объема dV : где ; – функция, комплексно сопряженная c . Волновую функцию называют амплитудой вероятности. Пси-функция непосредственно не измеряется на опыте.

Частица в одномерной бесконечно глубокой потенциальной яме.

Примером движения электрона в потенциальной «яме» является движение коллективизированных электронов внутри металла. Потенциальная энергия электрона вне и внутри одномерной прямоугольной потенциальной «ямы» U(x) имеет следующие значения где l – ширина «ямы»; стенки «ямы» бесконечно высокие, энергия отсчитывается от ее дна. 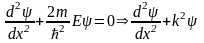Для одномерного случая в пределах «ямы», где U = 0, уравнение Шрёдингера упрощается: , где 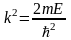. Общее решение уравнения имеет вид: 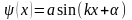, где а и – произвольные постоянные. Функция должна удовлетворять стандартным условиям. Видно, что

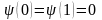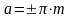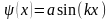однозначна и конечна. Она должна быть еще и непрерывной. За пределы «ямы» частица не проникает из-за бесконечно высоких стенок, поэтому волновая функция вне «ямы» равна нулю. Следовательно, на границах «ямы» непрерывная волновая функция также должна обращаться в нуль: . Из граничного условия получаем, что , где m = 0,1,2,3.... При m = 0, а также при четных значениях m имеем . При нечетных значениях m имеем 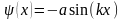. Поскольку физический смысл имеет квадрат модуля волновой функции 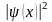, который от выбора значения m, т. е. от знака не зависит, то без потери общности можно считать, что = 0. После ещё некоторых мат. преобразований получаем минимальную энергию частицы в яме 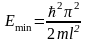. Следовательно, энергия частицы в бесконечно глубокой потенциальной «яме» принимает лишь определенные дискретные значения, т. е. квантуется, ее спектр – дискретный.

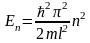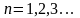Квантованные значения энергии называются уровнями энергии, а число , определяющее энергетические уровни частицы, называется квантовым

числом. Н. Бор сформулировал принцип соответствия: при больших квантовых числах выводы и результаты квантовой механики должны соответствовать классическим результатам.