3.5 Вопросы для самопроверки
Что называется первообразной?
Сформулируйте основные свойства неопределенного интеграла.
В чем заключается метод замены переменной?
Какие функции целесообразно интегрировать по частям? Почему?
Как разложить рациональную дробь на простейшие?
4 Определенный интеграл
Пусть
функция
определена на отрезке
.
Разобьём этот отрезок на части точками
Получим
частичных отрезков длиной
=
каждый.
В
каждом частичном отрезке выберем
произвольную точку
и вычислим в ней значение функции
.
Составим сумму произведений:
.
Эта
сумма называется интегральной
суммой
функции
на отрезке
.
Перейдем к пределу в последнем выражении,
когда максимальный из отрезков
.
Если
при этом сумма
имеет предел
,
не зависящей от способа разбиения
отрезка
на части и от выбора точек
в них, то число
называют определенным
интегралом
от функции
на отрезке
:
В таких случаях функцию называют интегрируемой на отрезке и для нее справедлива теорема, утверждающая, что любая непрерывная на отрезке функция, является интегрируемой.
4.1 Основные свойства определенного интеграла
1)
; 2)
;
3)
;
4)
;
5)
,
где
-
постоянная.
4.2 Правила вычисления определенного интеграла
Формула Ньютона-Лейбница:
,
где - первообразная для .
Интегрирование по частям:
,
где
и
-
непрерывные и дифференцируемые функции
на отрезке
.
Замена переменной:
,
где
-
функция, непрерывная вместе со своей
производной
на отрезке
.
4)
Пример 29 Вычислить:
.
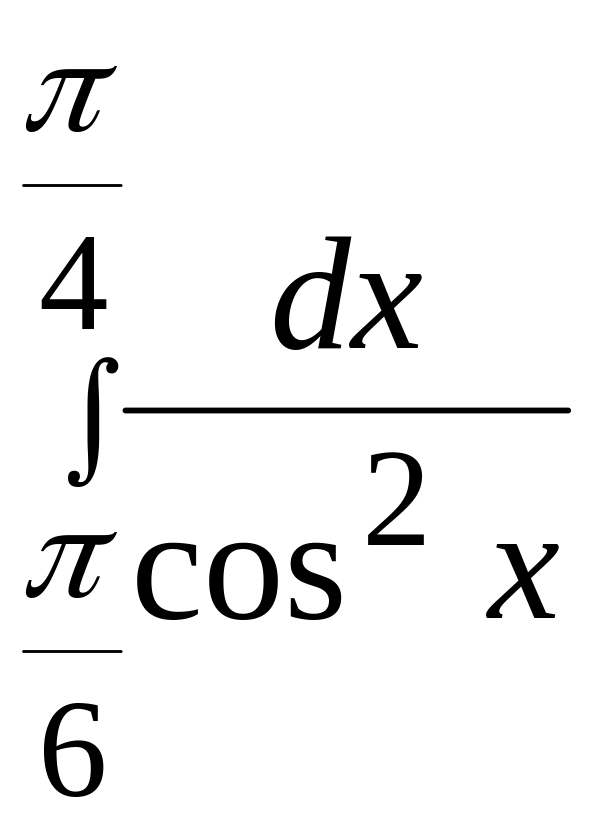Решение.
По формуле Ньютона-Лейбница будем иметь:
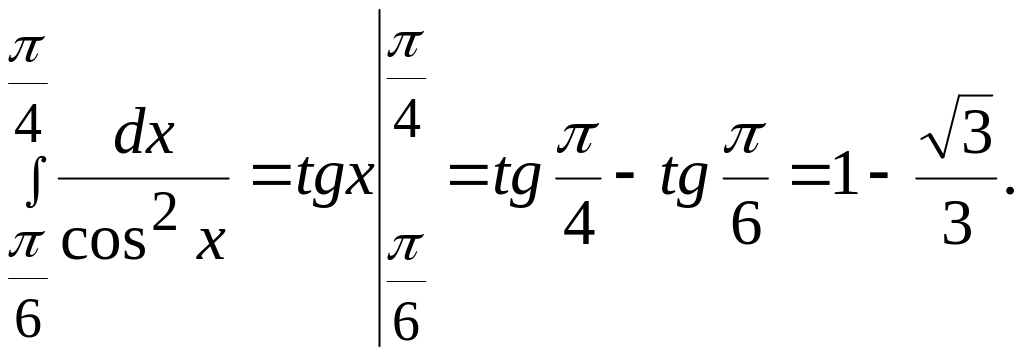
Пример 30. Вычислить:
.
Решение.
Используем формулу интегрирования по частям:
=
Пример 31 Вычислить:
.
Решение.
Сделаем
замену переменной:
;
;
.
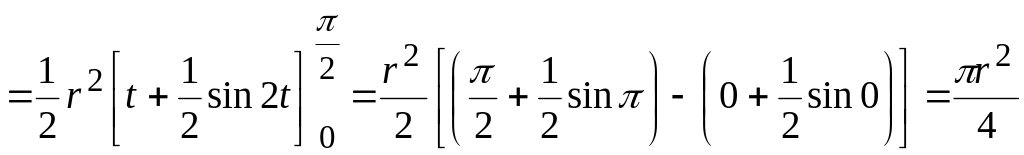Приложения определенного интеграла
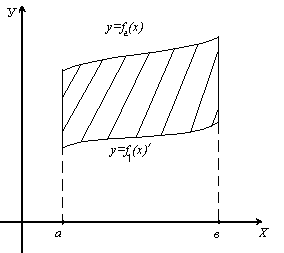
4.3.1 Вычисление площадей плоских фигур
Используя геометрический смысл
определенного интеграла, нетрудно
получить формулу для вычисления площади
плоской фигуры, ограниченной кривыми
и прямыми
:
.
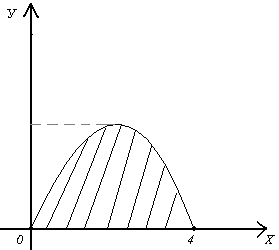
Пример 32
Вычислить площадь фигуры, ограниченной
параболой
и осью
.
Решение.
Парабола пересекает ось
в точках
и
,
.Поэтому:
(кв.ед.).
4.3.2 Вычисление объемов тел вращения
При вращении криволинейной трапеции,
ограниченной линиями:
,
,
;
вокруг оси
,
получим объем тела вращения:
.
Пример 33
Найти
объем тела, образованного вращением
вокруг оси
фигуры, ограниченной кривой
и прямой
.
Решение.
Для построения кривой найдем точки:
при
,
;
при
,
.
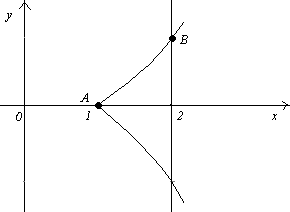
А(1,0); В(2,1)
4.3.3 Вычисление длины дуги плоской кривой
Если
кривая
имеет непрерывную производную на отрезке
,
то длина дуги этой кривой находится по
формуле:
.
Пример 34
Найти
длину дуги кривой
от
до
(
).
Решение.
Найдем
.
Тогда
.
4.4 Вопросы для самопроверки
Что называется интегральной суммой для функции на отрезке ?
Что называется определенным интегралом?
Каковы геометрический и физический смыслы определенного интеграла?
Назовите основные свойства определенного интеграла.
Назовите основные методы (правила) вычисления определенного интеграла.
Перечислите основные приложения определенного интеграла.
Индивидуальные задания для контрольной работы №2
Задача №1
Найти производные функций
1.
а)
, б)
,
в)
, г)
,
д)
.
2.
а)
, б)
,
в)
, г)
,
д)
.
3.
а)
, б)
,
в)
,
г)
.
д)
.
4.
а)
, б)
,
в)
, г)
,
д)
.
5.
а)
, б)
,
в)
, г)
,
д)
.
6.
а)
, б)
,
в)
, г)
,
д)
.
7.
а)
, б)
,
в)
, г)
,
д)
.
8.
а)
, б)
,
в)
, г)
,
д)
.
9.
а)
, б)
,
в)
, г)
,
д)
.
10.
а)
, б)
,
в)
, г)
,
д)
.
11.
а)
, б)
,
в)
, г)
,
д)
12.
а)
, б)
,
в)
, г)
,
д)
13.
а)
, б)
,
в)
, г)
,
д)
14.
а)
, б)
,
в)
, г)
,
д)
15.
а)
, б)
,
в)
, г)
,
д)
16.
а)
, б)
,
в)
, г)
,
д)
17.
а)
, б)
,
в)
, г)
,
д)
18.
а)
б)
в)
г)
,
д)
19.
а)
, б)
,
в)
, г)
,
д)
20. а)
, б)
,
в)
, г)
,
д)
Задача №2
Исследовать функцию методами дифференциального исчисления и построить ее графики:
1.
.
7.
.
14.
.
2.
. 8.
.
15.
.
3.
.
9.
.
16.
.
4.
. 10.
.
17.
.
5.
. 11.
.
18.
.
6.
. 12.
.
19.
.
13.
.
20.
.
Задача №3
Найти неопределенные интегралы способом подстановки (методом замены переменного).
1.
7.
14.
2.
8.
15.
3.
9.
16.
4.
10.
17.
5.
11.
18.
6.
12.
19.
13.
20.
