- •Основные понятия теории вероятности
- •2. Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.
- •3. Теория сложения вероятностей.
- •4. Условная вероятность.Св-ва.Т.Умножения.
- •6. Формула Байеса.
- •7. Повторные испытания.Схема Бернулли.
- •8. Повторные испытания. Схема Пуассона.
- •9. Случайные величины.Ряд распределения.
- •11. Числовые характеристики случайной величины
- •12. Моменты случайных величин.
- •Вычисление моментов
- •13. Равномерное распределение случайных величин. Плотность распределения.Вероятность попадания на интервал.
- •15. Вероятность попадания случайной величины в заданный интервал
- •14. Распределение Бернулли.
- •15. Распределения Пуассона.
- •16. Нормальное распределение.
- •17. Вероятность попадания случайной велечины на интервал.
- •19. Центральная предельная теорема
12. Моменты случайных величин.
Момент случайной величины — числовая характеристика распределения данной случайной величины.
Если
дана случайная величина ![]() определённая
на некотором вероятностном
пространстве,
то:
определённая
на некотором вероятностном
пространстве,
то:
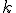 -м начальным моментом
случайной величины
где
-м начальным моментом
случайной величины
где 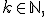 называется
величина
называется
величина
![]()
если математическое
ожидание ![]() в
правой части этого равенства определено;
в
правой части этого равенства определено;
-м центральным моментом случайной величины
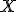 называется
величина
называется
величина
![]()
-м факториальным моментом случайной величины называется величина
![]()
если математическое ожидание в правой части этого равенства определено.
Вычисление моментов
Моменты могут быть вычислены напрямую через определение путём интегрирования соответствующих степеней случайной величины. В частности, для абсолютно непрерывного распределения с плотностью
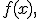 имеем:
имеем:
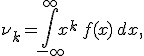
если 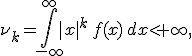
а для дискретного
распределения с функцией
вероятности ![]()
![]()
если ![]()
Также моменты случайной величины могут быть вычислены через ее характеристическую функцию
 :
:
![]()
Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов
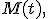 то
моменты могут быть вычислены по следующей
формуле:
то
моменты могут быть вычислены по следующей
формуле:
![]()
13. Равномерное распределение случайных величин. Плотность распределения.Вероятность попадания на интервал.
Непрерывная случайная
величина Х имеет
равномерное распределение на отрезке
[a, b],
если ее плотность имеет следующий
вид:
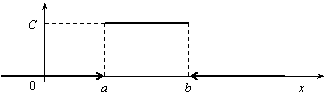
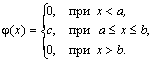 График плотности распределения показан
на рис. 2.9.
φ(х)
График плотности распределения показан
на рис. 2.9.
φ(х)
Плотность распределения (дифференциальная функция распределения)
Плотность
распределения случайной величины ![]() определяется
по формуле
определяется
по формуле![]() .
Существует только для непрерывной
случайной величины. Для нее выполняется
условие нормировки:
.
Существует только для непрерывной
случайной величины. Для нее выполняется
условие нормировки: ![]() (площадь
под кривой равна 1).
(площадь
под кривой равна 1).
15. Вероятность попадания случайной величины в заданный интервал
Может быть вычислена двумя способами:
1)
через функцию распределения ![]()
2)
через плотность распределения 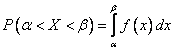
14. Распределение Бернулли.
случайная
величина ![]() имеет распределение
Бернулли с
параметром
имеет распределение
Бернулли с
параметром ![]() ,
и пишут:
,
и пишут: ![]() ,
если
принимает
значения 1 и 0 с вероятностями
и
,
если
принимает
значения 1 и 0 с вероятностями
и ![]() соответственно.
Случайная величина
с
таким распределением равна числу
успехов в одном испытании схемы
Бернулли с
вероятностью успеха
:
ни одного успеха или один успех. Таблица
распределения
имеет
вид:
соответственно.
Случайная величина
с
таким распределением равна числу
успехов в одном испытании схемы
Бернулли с
вероятностью успеха
:
ни одного успеха или один успех. Таблица
распределения
имеет
вид:
|
0 |
1 |
|
|
|
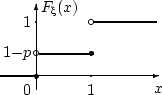
Функция распределения случайной величины такова:
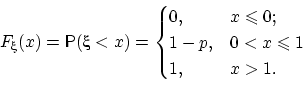
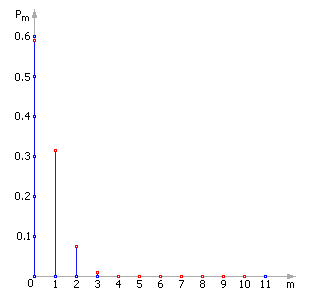
15. Распределения Пуассона.
Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и приp –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
![]()
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
Pm = Cnm · pm · (1 – p)n – m
может быть написан, если положить p = a/n, в виде
![]()
или
![]()
Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению сn. Произведение
![]()
весьма близко к единице. Это же относится к величине
![]()
Величина
![]()
очень близка к e–a. Отсюда получаем формулу:
|
Рис. 27.3. График распределения Пуассона при p = 0.05 и n = 10