
- •Основные понятия теории вероятности
- •2. Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.
- •3. Теория сложения вероятностей.
- •4. Условная вероятность.Св-ва.Т.Умножения.
- •6. Формула Байеса.
- •7. Повторные испытания.Схема Бернулли.
- •8. Повторные испытания. Схема Пуассона.
- •9. Случайные величины.Ряд распределения.
- •11. Числовые характеристики случайной величины
- •12. Моменты случайных величин.
- •Вычисление моментов
- •13. Равномерное распределение случайных величин. Плотность распределения.Вероятность попадания на интервал.
- •15. Вероятность попадания случайной величины в заданный интервал
- •14. Распределение Бернулли.
- •15. Распределения Пуассона.
- •16. Нормальное распределение.
- •17. Вероятность попадания случайной велечины на интервал.
- •19. Центральная предельная теорема
8. Повторные испытания. Схема Пуассона.
(теорема
Пуассона(1)). Пусть ![]() и
и ![]() так,
что
так,
что ![]() .
Тогда для любого
.
Тогда для любого ![]() вероятность
получить
вероятность
получить ![]() успехов
в
успехов
в ![]() испытаниях
схемы Бернулли с вероятностью
успеха
испытаниях
схемы Бернулли с вероятностью
успеха ![]() стремится
к величине
стремится
к величине ![]() :
:

Доказательство. Положим ![]() .
Тогда
.
Тогда ![]() и
и
|
(8) |
В соотношении (8) мы
воспользовались тем, что ![]() и
замечательным пределом
и
замечательным пределом ![]() .
Докажем последнее свойство:
.
Докажем последнее свойство:
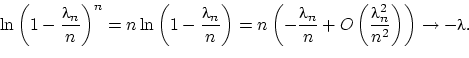
QED
Определение
25. Набор
чисел ![]() называется распределением
Пуассона с
параметром
называется распределением
Пуассона с
параметром ![]() .
.
9. Случайные величины.Ряд распределения.
Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз. Различают дискретные и непрерывные случайные величины. Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4). Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин. Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной.
Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины. Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:
Х |
х1 |
х2 |
… |
хn |
… |
Р |
р1 |
р2 |
… |
рn |
… |
Такая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х1, х2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, … , n) образуют полную группу попарно независимых событий. Следовательно, р1 + р2 + … + рn = 1.
10.Ф-я распределения,плотности.
Если
называется функцией
распределения случайной величины
.
Здесь Функция распределения любой случайной величины обладает следующими свойствами:
. Функция распределения содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения,которую часто называют просто распределением. Чаще используется термин распределение.
Если функция распределения
Если функция распределения
дифференцируема,
то более наглядное представление о
случайной величине дает плотность
вероятности случайной величины
Отсюда, в частности, следует, что для
любой случайной величины
Вероятность того, что значение случайной
величины
попадает
в интервал
|
Дифференциальная функция распределения (плотность вероятности)
![]()
![]()
![]()
![]()
где F(x) - интегральная функция.
Свойства:
1) ![]()
![]() ;
;
2) ![]()
![]()
![]() ;
;
3) ![]()
![]()
![]() ;
;
4) ![]()
![]()
![]()
![]()
![]() .
.

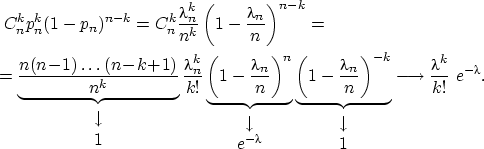
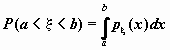 или
или