4.5 Математичне моделювання реактора з киплячим (псевдозрідженим) шаром

С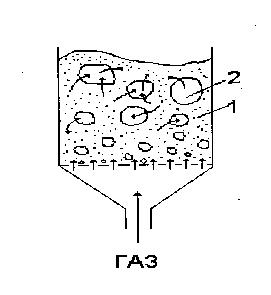 еред математичних моделей реакторів з киплячим шаром каталізатора, що використовуються у практиці розрахунків, найбільше поширення одержала двохфазна модель. Відповідно до цієї моделі (рис. 4.1), киплячий шар розглядається як двохфазна система, що складається із суспензії, утвореної з твердих частинок каталізатора, обтічних потоком газу (щільна фаза 1), і фази пузирів (2), що практично не містить твердих частинок.

Рис.4.1. Киплячий шар каталізатора: схема двохфазної моделі

(1 — щільна фаза, 2 — фаза пузирів);

Передбачається, що структура потоку газу в щільній фазі відповідає уявленням про неповне подовжнє змішування. Подовжнє змішування між пузирями, а також контакт пузирів з твердими частинками каталізатора в першому наближенні з розгляду виключається, тобто хімічні перетворення відбуваються тільки в щільній фазі. Це обумовлено тим, що промислові реактори працюють з великими числами псевдоожиженя, при яких швидкість підйому газових пузирів перевищує швидкість у щільній фазі. Між фазами йде безупинний обмін газом, який характеризується коефіцієнтом міжфазового обміну, в основному за рахунок руйнування й утворення пузирів, переносу газу твердими частками і т.п. За рахунок інтенсивного перемішування частинок каталізатора, реактор ізотермичний по висоті і радіусу.

Згідно двохфазній моделі, матеріальний баланс по i-му компоненту описується системою рівнянь:

1/Ре∙d2хi/dξ2 - dxi/dξ - Nu(xi - уi) + (LK/ώ1) f(x1,...,хn) = 0 (4.34)

dyi/dξ - Nu q/(1 - q) (хi - уi) = 0 (4.35)

zi=qxi + (1 - q)уi (i=1,...,nk) (4.36)

Рівняння (4.34) - (4.36) записані для щільної фази, фази пузирів і сумарної концентрації i-го компонента;

де хi й уi – концентрації i-го компонента в щільній фазі і фазі пузирів;

Ре = ω1L/ D – критерій Пеклє подовжнього перемішування в щільній фазі;

Nu = βL/ω1 – критерій міжфазового обміну; β – коефіцієнт міжфазового обміну; L – висота шару; D – коефіцієнт подовжнього перемішування в щільній фазі;

ω1 – лінійна швидкість газу в щільній фазі; υ – витрата газу на вході в реактор;

υ1 – витрата газу, що проходить через щільну частину;

q = υ1/υ – об'ємна частка потоку газу, що проходить через щільну фазу.

Граничні умови:

1/Pe dxi/dξ xi xНi

yi = xНi ; dx/dξ = 0 ,

де х_нi – концентрация i- го компонента на входе в кипящий слой.

Рівняння (4.34) і (4.35) є звичайними диференціальними рівняннями другого і першого порядку з граничними умовами на різних кінцях шару. Для розв’язування таких задач переходять до нестаціонарного процесу з перетворенням рівнянь у звичайних похідних у рівняння з частинними похідними. Нестаціонарну систему рівнянь інтегрують до встановлення стаціонарного стану. Надалі будемо розглядати однокомпонентну реакцію, оскільки перенесення результатів на загальний випадок не викликає труднощів.

Після переходу до нестаціонарної задачі маємо систему рівнянь

1/Pe∙(d2x/dξ2) - dx/dξ + Nu(y - x) + ω(x) = dx/dt; (4.37)

-dy/dξ + Nu q/(1 - q) (x- y) = dy/dt (4.38)

з граничними умовами:

1/Pe dx/dξ x xн

yi = xн ; dx/dξ = 0

початкові умови: t = 0; x = y = x0.

Для розв’язування рівнянь (4.37 – 4.38) використовуємо метод кінцевих різниць чи метод сіток, що є універсальним і ефективним для розв’язувння багатьох задач математичної фізики. Він дозволяє зводити наближене рішення рівнянь у частинних похідних до рішення систем алгебраїчних рівнянь.

Будемо вважати, що рішення вихідної задачі для диференціального рівняння існує і має потрібне число похідних, що забезпечує максимальний порядок апроксимації. Для написання різницевої схеми, яка приблизно відповідає диференціальному рівнянню, потрібно зробити наступне:

• замінити область безперервної зміни аргументу областю дискретної його зміни;

• замінити диференціальний оператор деяким різницевим оператором;

• сформулювати різницеві аналоги для крайових умов і початкових даних.

У результаті одержимо алгебраїчну систему рівнянь. Таким чином, задача про чисельне рішення вихідного диференціального рівняння зводиться до знаходження рішення отриманої алгебраїчної системи.

При чисельному рішенні задачі неможливо одержати різницеве рішення для всіх значень аргументу, які змінюється усередині деякої області. Тому виберемо в цій області деяку кінцеву безліч крапок, і наближене рішення будемо шукати тільки в них. Така безліч крапок називається сіткою, а самі крапки вузлами сітки.

На прямокутній сітці (рис.4.2) ξi = ih, tk = kτ

(і = 0,1,...,n; k = 0,1, . . .) рівняння (4.37) і (4.38) апроксимуємо неявною різницевою схемою.

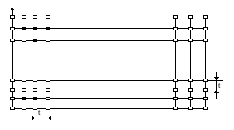
Рис.4.2. Схема сітки

Тоді задачу наближеного інтегрування :

- Nu (Xik-1 – Уk-1) + ω (Xik-1) (4.39)

(4.40)

i = 1, . . . ,n; k=1, 2, . . .

з граничними і початковими умовами

при ξ=0

(Х₁^k - Х₀^k) / h = Pe(X₀^k - Х_н); Y₀^k=X_Н; (4.41)

при ξ=1

(Х_n^k- X_n-1^k) / h = 0; (4.42)

при t = 0; X₁⁰ = Х_н; У_i⁰= Х_н

представимо у виді

A₁X_i+1^k - B₁ X_i^k + C₁ X_i-1^k = -φ_1i^k-1; (4.43)

-Y_i+1^k - B₂ Y_i^k + У_i-1^k=-φ_2i^k-1; (4.44)

де

A₁= (2h - h²Ре)/2h³ Ре; B₁ = (2τ + h²Pe)/τh²Pe; C₁ = (2h+ h²Ре)/2h³Ре;

φ_1i^k-1 = X_i^k-1/τ - Nu(X_i^k-1 - У_i^k-1 ) + ω(X_i^k-1 ); B₂ = 2h/τ;

φ_2i^k-1 = 2h/τ∙Y_i^k-1 + (2hq)/(1-q)∙Nu(X_i^k-1-У_i^k-1).

Алгебраїчні рівняння.(4.39) і (4.40) можна вирішити методом прогону. Відповідно до цього методу, кожне з них заміняють системою трьох рекурентних співвідношень, що знаходять у такий спосіб:

запишемо для X_i^k-1 і Y_i^k-1 вираз виду:

X_i^k-1 = P₁i X_i^k + R_1i; У_i^k-1=P_2iY_i^k+R_2i

і підставимо їх у рівняння (4.43) і (4.44). У результаті одержуємо:

X_i^k = P_1i+1X_i+1^k + R_1i+1; i = n-1,n-2,...,0; k = 1,2,… (4.45)

P_1i+1 = А₁/(В₁ - С₁ Р_1i); i = 1, 2,..., n-1 (4.46)

R_1i+1 = (C₁R_1i + φ_1i^k-1)/(B₁ - C₁P_1i); i = 1,2,…,n-1;k = 1,2,…. (4.47)

Y_i^k = Р_2i+1 Y_i+1^k + R_2i+1; i = n-1,...,0; k = 1,2,… (4.48)

P_2i+1 = 1/(Р_2i - В₂); (4.49)

R_2i+1 = (R_2i + φ_2i^k-1)/(В₂ - Р_2i); (4.50)

Співмножники P_1i, R_1i, P_2i, R_2i знаходимо з рівнянь (4.41), (4.45) і (4.48)

Р_1i = (1 + h Ре(Х_н/ X_1i^k ))/ l + h Ре; R_1i=0;

P²ⁱ=X_H/У_i^k; R_2i=0,

а R_1n, P_1n, R_2n, Р_2n находимо з рівнянь (4.11), (4.12) и (4.15):

X_n-1^k = Х_n^k; Х_n^k = R_1n/(1 - P_1n), если R_1n ≠ 0

X_n^k = max X, если R_1n = 0;

Y_n^k = R_2n/(1 - Р_2n), если R_2n ≠ 0;

Y_n^k = maxХ, если R_2n = 0.

При k = 0 и 1≤ i ≥ n; Х₁₀ = Х_H и Y₁₀ = Х_H

Рівняння (4.45 – 4.50) із граничними і початковими умовами вирішують у наступній послідовності. Спочатку по рівняннях (4.46, 4.47 і 4.49, 4.50) при прямуванні уздовж сітки праворуч розраховують прогонні коефіцієнти P_i і R_i. Потім по рівняннях (4.45) і (4.50) при прямуванні по сітці ліворуч знаходяться n-1 значень X_i і Y_i. Весь цикл розрахунку повторюють до встановлення стаціонарного стану, тобто до виконання умови |X_i^k – X_i^k-1|< , де  - задана точність “стаціонування задачі”.

Для забезпечення стабільності обчислень по рекурентних формулах (4.45 і 4.47) рекомендується вибирати крок сітки по просторовій координаті h<2/Ре_мах, а по часовій координаті – τ ≤ 1/ Nu_max; тут Ре_мах і Nu_max - максимально можливе значення критерію Пеклє і міжфазового обміну.

Швидкість реакції окислювання оксиду сірки (IV) описуємо рівнянням:

r = K .

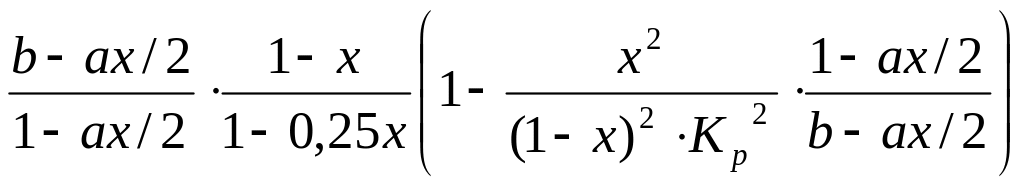де а, b - початкові концентрації SO₂ і O₂;

x - ступінь перетворення SO₂.

Константа рівноваги реакції розраховується по рівнянню:

K = 104905,5/T-4,6455;

К - константа швидкості:

К = 5,2 при Т > 803

К = 10(0,65-2530(1/T-1/787)) при 773 < Т < 803

K = 10(0,525-3750(1/T-1/763)) при Т < 773

Додаток 5