По правилу сложения матриц
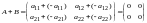 ,
,
аксиома 4 имеет место.
Итак, аксиомы 1 - 4 справедливы. Аналогично проверяется выполнение аксиом 5 - 8. Таким образом, совокупность всех квадратных матриц 2-го порядка - линейное пространство.
Следует отметить, что, вводя линейное пространство, мы отвлекаемся не только от конкретной природы изучаемых объектов, но и от конкретных правил образования суммы векторов и произведения на число, - важно лишь, чтобы эти правила удовлетворяли аксиомам, сформулированным в определении линейного пространства.
Укажем некоторые следствия из аксиом.
Единственность нулевого элемента.
Действительно,
допустим,
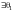 и
и
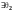 - нулевые элементы, следовательно,
- нулевые элементы, следовательно,
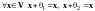 .
.
Имеем
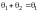 (так как
(так как
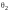 - нулевой), но
- нулевой), но
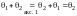 (так как
(так как
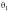 - нулевой), следовательно,
- нулевой), следовательно,
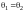 .
.
2. Единственность противоположного элемента.
Пусть
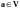 и
и
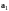 ,
,
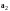 - противоположные элементы для
- противоположные элементы для
 ,
т.е.
,
т.е.
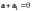 ,
,
 .
.
Рассмотрим
вектор
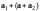 .
Имеем
.
Имеем
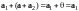 .
.
С другой стороны,
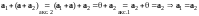 .
.
Теперь
всюду далее противоположный элемент
для
будем обозначать
 .
.
3. Существование и единственность разности.
Дадим
определение разности. Для любых двух
векторов
и
 назовем разностью
и
такой вектор
назовем разностью
и
такой вектор
 ,
что
,
что
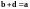 .
Обозначим
.
Обозначим
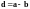 .
.
Положим
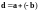 .
.
Имеем
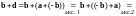
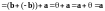 .
.
Следовательно, вектор удовлетворяет определению разности.
Покажем, что он единственный вектор, удовлетворяющий этому определению.
Пусть
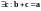 .
.
К
обеим частям последнего равенства
прибавим вектор
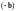 :
:
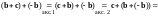
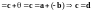 -
-
таким образом, вектор - единственный.
Для любого вещественного числа

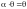 .
.
5.
Для любого вектора
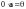 .
.
6.
Если
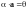 ,
то либо
,
то либо
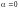 ,
либо
,
либо
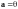 .
.
Для любого вещественного числа и любого справедливы соотношения:
7.
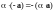 ;
;
8.
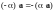 .
.
Следствия 4 - 8 докажите самостоятельно.
10.2. Базис линейного пространства
Определение 2. Пусть
-
линейное пространство. Вектор
 называется линейной комбинацией векторов
называется линейной комбинацией векторов
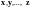 ,
если найдутся такие числа
,
если найдутся такие числа
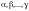 ,
что
,
что
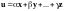 .
.
Определение 3. Система векторов , принадлежащих линейному пространству , называется линейно зависимой, если найдутся такие числа , не все равные нулю одновременно, что выполняется равенство
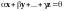 .
.
Определение линейно зависимой системы векторов можно дать в следующей эквивалентной форме, иногда более удобной.
Определение 3'. Система векторов , принадлежащих линейному пространству , называется линейно зависимой, если один из векторов является линейной комбинацией остальных.
Определение 4. Система векторов , принадлежащих линейному пространству , называется линейно независимой, если из равенства
следует, что
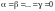 .
.
Пример
3. Пусть
- линейное пространство всех матриц
порядка
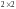 .
Доказать, что векторы
.
Доказать, что векторы
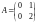 и
и
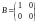
линейно независимы.
Решение. Рассмотрим
линейную комбинацию
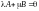 :
:
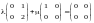 .
(10.1)
.
(10.1)
Привлекая правила умножения матриц на число и сложения матриц, получим
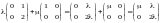 .
(10.2)
.
(10.2)
Равенства (10.1) и (10.2) дают

откуда
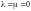 ,
следовательно,
и
линейно независимы.
,
следовательно,
и
линейно независимы.
Справедливы следующие два утверждения, доказательство которых приведено в лекции 1.
Теорема 1. Всякая система векторов, содержащая нулевой вектор, линейно зависима.
Теорема
2. Всякая система векторов
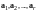 ,
содержащая линейно зависимую подсистему
векторов,
,
содержащая линейно зависимую подсистему
векторов,
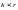 ,
линейно зависима.
,
линейно зависима.
Определение 5. Система
векторов
 линейного пространства
называется базисом в
,
если:
линейного пространства
называется базисом в
,
если:
1) линейно независима;
2)
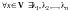 (вещественные числа):
(вещественные числа):
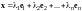 .
(10.3)
.
(10.3)
Правая часть равенства (10.3) называется разложением вектора по базису , а числа - координатами вектора в базисе .
Приведем примеры базисов в конкретных линейных пространствах.
Пример 4. - линейное пространство всех геометрических векторов, базисом являются любые три некомпланарных вектора.
Пример
5.
- линейное пространство всех многочленов
степени
.
Показать, что базисом является система
векторов
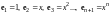 .
.
Решение. Составим
линейную комбинацию векторов
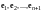 и приравняем ее нулевому вектору:
и приравняем ее нулевому вектору:
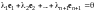 ,
,
или
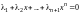 .
.
Имеет место основная теорема алгебры: всякий многочлен степени с действительными коэффициентами имеет ровно корней, при этом каждый корень считается столько раз, какова его кратность. Это утверждение означает, что равенство возможно не более, чем в точках, т.е. не может выполняться тождественно (как равенство между векторами в ).
Следовательно, допущение,
что линейная комбинация векторов
с коэффициентами
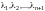 равна нулевому вектору
,
влечет
равна нулевому вектору
,
влечет
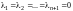 ,
а это означает, что
линейно независимы.
,
а это означает, что
линейно независимы.
Пусть
 - произвольный многочлен степени
.
В последней записи
представлен в виде линейной комбинации
векторов
,
что вместе с линейной независимостью
этих векторов доказывает, что система
- базис в пространстве многочленов
степени
(в соответствии с определением 5).
- произвольный многочлен степени
.
В последней записи
представлен в виде линейной комбинации
векторов
,
что вместе с линейной независимостью
этих векторов доказывает, что система
- базис в пространстве многочленов
степени
(в соответствии с определением 5).
Пример 6. - линейное пространство всех квадратных матриц порядка 2. Показать, что базисом является система
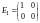 ,
,
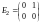 ,
,
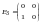 ,
,
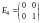 .
.
Решение.
Убедимся в том, что система
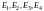 линейно независима. Составим линейную
комбинацию и приравняем ее
:
линейно независима. Составим линейную
комбинацию и приравняем ее
:
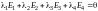 ,
,
или
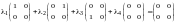 ,
,
откуда
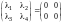 .
.
Последнее равенство
дает
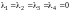 ,
следовательно, система векторов
линейно независима.
,
следовательно, система векторов
линейно независима.
Пусть - произвольный вектор из .
Привлекая определения сложения матриц и умножения матрицы на число, получим
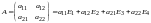 ,
,
т.е. любой вектор из можно представить в виде линейной комбинации . В соответствии с определением 5 это вместе с доказанной выше линейной независимостью означает, что - базис.
Упражнение.
Доказать, что в линейном пространстве
 система векторов
система векторов
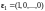 ,
,
 ,
…,
,
…,
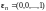 является базисом.
является базисом.
Теорема 3. Пусть
- линейное пространство,
- базис в
,
 .
Координаты
относительно базиса определены
однозначно.
.
Координаты
относительно базиса определены
однозначно.
Доказательство. Пусть
,
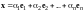 и
и
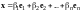 .
.
Имеем
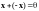 .
.
С другой стороны,
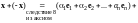
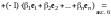
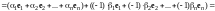
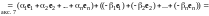
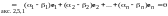 .
.
Откуда в силу линейной
независимости векторов
следует
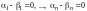 ,
т.е.
,
т.е.
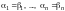 .
.
Допустив, что вектор имеет два разложения по базису , мы получили, что эти разложения совпадают, это и означает, что координаты вектора относительно базиса определены однозначно.
Теорема доказана.
Замечание. Доказательство Теоремы 3 почти дословно повторяет доказательство аналогичного утверждения для геометрических векторов (Теорема 6 в лекции 1). Как и при доказательстве Теорем 1 и 2 , не используется геометрическая природа векторов, а лишь понятия линейной зависимости и линейной независимости. Приведенную ниже Теорему 4 предлагаем доказать самостоятельно (см. Теорему 7 в Лекции 1).
Теорема 4. Пусть - линейное пространство, - базис в . При сложении любых двух векторов их соответствующие координаты складываются, при умножении вектора на число каждая координата умножается на это число.
Теорема 5. Пусть
- линейное пространство,
- базис в
.
Всякая система
векторов
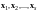 при
при
 линейно зависима.
линейно зависима.
Доказательство.
Достаточно доказать утверждение для
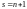 (если
(если
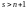 ,
сошлемся на теорему 2).
,
сошлемся на теорему 2).
Пусть
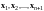 - произвольная система векторов в
.
- произвольная система векторов в
.
Случай 1. Среди есть , следовательно, система линейно зависима.
Случай
2.
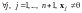 .
.
Так как система
- базис, существуют такие
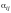
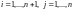 ,
что
,
что
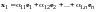 ,
,
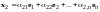 ,
(10.4)
,
(10.4)
……………………………………
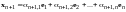 .
.
Среди чисел
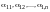 есть отличные от нуля (иначе
есть отличные от нуля (иначе
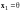 ).
Не ограничивая общности рассуждений,
можно считать, что
).
Не ограничивая общности рассуждений,
можно считать, что
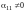 (в противном случае можно перенумеровать
базисные векторы), следовательно,
(в противном случае можно перенумеровать
базисные векторы), следовательно,
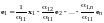 .
(10.5)
.
(10.5)
Подставив (10.5) во все равенства (10.4), начиная со второго, получим
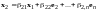 ,
,
…………………………………… (10.6)
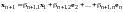 .
.
Векторы
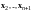 линейно выражаются через
линейно выражаются через
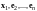 .
.
Если в первом равенстве
в системе (10.6)
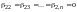 ,
то
,
то
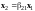 ,
и система векторов
,
и система векторов
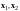 линейно зависима. Тогда, согласно теореме
2, система векторов
также линейно зависима.
линейно зависима. Тогда, согласно теореме
2, система векторов
также линейно зависима.
Если же среди
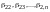 есть отличные от нуля, то, не ограничивая
общности рассуждений, считаем, что
есть отличные от нуля, то, не ограничивая
общности рассуждений, считаем, что
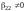 .
.
Из первого равенства в (10.6) имеем
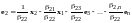 .
(10.7)
.
(10.7)
Подставим (10.7) во все
равенства (10.6), начиная со второго,
получим выражения
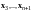 через
через
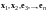 .
.
Процедуру повторим
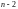 раза и придем к равенству
раза и придем к равенству
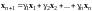 .
.
Один из векторов системы оказался линейной комбинацией остальных, следовательно, линейно зависимы.
Теорема доказана.
Следствие. Все базисы линейного пространства состоят из одного и того же числа векторов.
Действительно,
пусть
(I) и
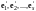 (II) - два базиса в
.
(II) - два базиса в
.
Допустим,
.
Так как система (I) - базис,
то в силу теоремы 5 это означает, что
система (II) линейно
зависима. Это противоречит тому, что
(II) - базис. Отсюда
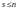 .
.
Допустим теперь, что
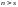 .
Так как система (II) - базис,
то в силу теоремы 5 это означает, что
система (I) линейно зависима.
Это противоречит тому, что (I)
- базис. Следовательно,
.
Так как система (II) - базис,
то в силу теоремы 5 это означает, что
система (I) линейно зависима.
Это противоречит тому, что (I)
- базис. Следовательно,
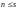 .
.
Вместе эти два заключения дают .
Определение 6. Число векторов в любом базисе линейного пространства называется размерностью линейного пространства.
Для размерности линейного
пространства
принято обозначение
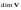 .
.
В рассмотренных примерах:
если - линейное пространство всех геометрических векторов пространства,
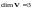 ;
;если - линейное пространство всех многочленов степени ,
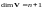 ;
;если - линейное пространство всех квадратных матриц порядка 2,
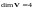 .
.
Лекция 11
Связь между базисами линейного пространства.
Линейные подпространства
Матрица перехода от базиса к базису. Связь координат одного и того же вектора в двух базисах. Линейные подпространства. Примеры |
11.1. Связь между базисами линейного пространства
Пусть
-
линейное пространство,
(I)
и
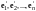 (II)
- два базиса в
.
(II)
- два базиса в
.
Так
как (I)
- базис, любой вектор из
,
в частности любой вектор системы (II),
можно представить в виде линейной
комбинации векторов системы (I),
т.е. найдутся такие числа
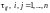 ,
что
,
что
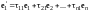
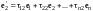
………………………………. (11.1)
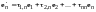
Определение 1. Матрица
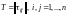 называется матрицей перехода от базиса
(I) к базису (II).
называется матрицей перехода от базиса
(I) к базису (II).
Замечание 1. Столбцы матрицы перехода , являются координатами в разложении векторов по базису (I).
Справедливость этого замечания непосредственно следует из равенств (11.1).
Замечание 2. Матрица перехода от базиса к базису является невырожденной матрицей.
Доказательство этого факта опустим.
Справедливо следующее утверждение.
Теорема 1. Пусть
- линейное пространство,
(I) и
(II) - два базиса в
,
 - матрица перехода от (I)
к (II),
,
и
- матрица перехода от (I)
к (II),
,
и
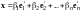 ,
тогда
,
тогда
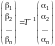 .
(11.2)
.
(11.2)
Доказательство.
Подставим в разложение
по базису (II) выражения
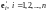 из (11.1), получим
из (11.1), получим
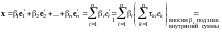
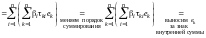
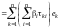 .
.
Последнюю сумму запишем развернуто:
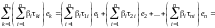
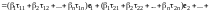
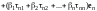 .
.
По условию , используя теорему о единственности разложения вектора по базису (теорема 3 в лекции 10), получим
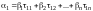 ,
,
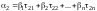 ,
,
……………………………………
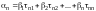 ,
,
что в матричном виде выглядит как равенство
 .
.
Отсюда следует
.
Теорема доказана.
Пример
1.
 - линейное пространство всех геометрических
векторов плоскости,
- линейное пространство всех геометрических
векторов плоскости,
 (I)
- произвольный декартов базис,
(I)
- произвольный декартов базис,
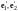 (II)
- декартов базис, полученный поворотом
векторов
(II)
- декартов базис, полученный поворотом
векторов
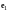 и
и
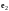 на угол
на угол
 против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).
против хода часовой стрелки. Найти
матрицу перехода от (I) к
(II) и связь координат
одного и того же вектора в (I)
и (II).
Имеем
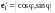 ,
,
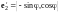 (рис. 11.1). Тогда
(рис. 11.1). Тогда
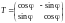
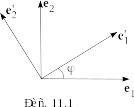 .
.
- матрица перехода от (I) к (II).
Найдем
 .
.
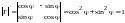 и
и
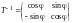 .
.
Формула (11.2) в этом случае имеет вид
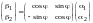 ,
,
где
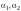 - координаты произвольного вектора
в базисе (I), а
- координаты произвольного вектора
в базисе (I), а
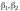 – координаты этого же вектора в базисе
(II).
– координаты этого же вектора в базисе
(II).
(Сравните с формулами (5.24) в Лекции 5).
Пример
2.
- произвольное линейное пространство,
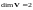 .
Векторы
.
Векторы
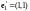 ,
,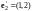 и
и
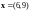 заданы своими координатами в некотором
базисе
.
Доказать, что система
- базис в
,
и найти координаты вектора
в базисе
.
заданы своими координатами в некотором
базисе
.
Доказать, что система
- базис в
,
и найти координаты вектора
в базисе
.
Сначала докажем, что
система
- базис. Рассмотрим линейную комбинацию
векторов
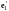 и
и
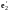 ,
равную нулевому вектору
:
,
равную нулевому вектору
:
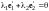 .
.
Покоординатно последнее равенство запишется в виде системы двух уравнений:
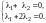 (11.3)
(11.3)
Определитель системы
(11.3)
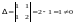 ,
следовательно, система (11.3) имеет
единственное решение
,
следовательно, система (11.3) имеет
единственное решение
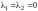 .
.
Итак, допустив, что линейная комбинация векторов и равна , мы с необходимостью получили, что коэффициенты этой линейной комбинации равны нулю. Это означает, что система векторов линейно независима, а так как , векторы являются базисом в . Обозначим этот базис (II).
Найдем матрицу перехода от (I) к (II).
В силу определения 1
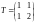 (координаты векторов
и
в (I) располагаем по
столбцам).
(координаты векторов
и
в (I) располагаем по
столбцам).
Обозначим через
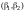 координаты
вектора
в (II).
координаты
вектора
в (II).
Воспользуемся теоремой 1. Найдем . Имеем
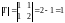 ,
,
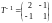
и по формуле (11.2) получим
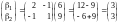 .
.
Итак,
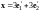 .
.
11.2. Линейные подпространства
Определение 2. Пусть
- линейное пространство. Непустое
подмножество
 линейного пространства
(
линейного пространства
(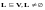 )
называется линейным подпространством
в
,
если выполняются два условия:
)
называется линейным подпространством
в
,
если выполняются два условия:
1)
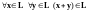 ;
;
2)
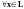 при любом вещественном числе
при любом вещественном числе
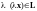 .
.
Пример
3. Пусть
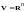 - линейное пространство всех
арифметических
-мерных
векторов
- линейное пространство всех
арифметических
-мерных
векторов
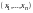 ;
- совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
;
- совокупность всех векторов, у которых
первая и последняя компоненты равны
нулю, т.е. векторов вида
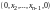 .
- подпространство в
.
.
- подпространство в
.
Действительно, пусть
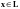 и
и
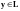 ,
следовательно, по определению
,
следовательно, по определению
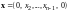 и
и
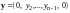 .
По правилу сложения векторов в
.
По правилу сложения векторов в
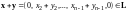 и, таким образом, сумма любых двух
векторов из
принадлежит
.
и, таким образом, сумма любых двух
векторов из
принадлежит
.
Пусть
и
- произвольное вещественное число.
Но
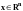 (так как
(так как
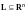 ),
следовательно, по правилу умножения
вектора на число в
),
следовательно, по правилу умножения
вектора на число в
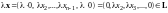 и вместе с любым вектором произведение
его на
тоже принадлежит
.
В соответствии с определением 2 это
означает, что
- линейное подпространство в
и вместе с любым вектором произведение
его на
тоже принадлежит
.
В соответствии с определением 2 это
означает, что
- линейное подпространство в
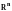 .
.
Замечание. Если - линейное подпространство в , то само является линейным пространством относительно введенных в операций сложения и умножения на число.
Действительно, требования 1) и 2) в определении 2 означают, что в определены операции сложения векторов и умножения вектора на число.
Аксиомы 1 и 2 выполняются в , так как они имеют место в . Убедимся в справедливости аксиомы 3.
Пусть
,
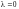 ,
следовательно, согласно условию 2)
,
следовательно, согласно условию 2)
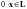 ,
но по следствию 5 из аксиом в
,
но по следствию 5 из аксиом в
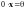 ,
таким образом,
,
таким образом,
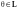 и в
справедлива аксиома 3.
и в
справедлива аксиома 3.
Пусть
,
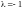 .
Следовательно, согласно условию 2)
.
Следовательно, согласно условию 2)
 ,
но по следствию 8 из аксиом в
,
но по следствию 8 из аксиом в
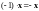 ,
таким образом,
,
таким образом,
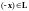 и в
справедлива аксиома 4.
и в
справедлива аксиома 4.
Аналогично проверяется справедливость аксиом 5 - 8, следовательно, - линейное пространство.
Пусть
- произвольное линейное пространство,
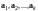 - некоторая система векторов в
.
Рассмотрим совокупность всех векторов
вида
- некоторая система векторов в
.
Рассмотрим совокупность всех векторов
вида
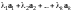 ,
где
,
где
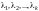 принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
принимают всевозможные вещественные
значения. Обозначим множество этих
векторов
 .
называется линейной оболочкой
векторов
.
является подпространством в
.
.
называется линейной оболочкой
векторов
.
является подпространством в
.
Действительно,
(так как, например, сами векторы
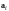 ,
,
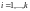 ,
принадлежат
).
,
принадлежат
).
Пусть
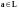 ,
,
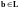 ,
следовательно, по определению
,
следовательно, по определению
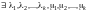 такие, что
такие, что
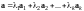 ,
,
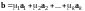 .
.
Имеем
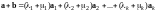 и
и
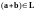 .
.
Пусть
,
 - произвольное вещественное число.
- произвольное вещественное число.
Имеем
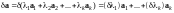 и
и
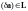 .
.
Таким образом, выполняются условия 1) и 2) определения 2 и является линейным подпространством в .
Говорят, что порождено системой векторов или "натянуто" на систему .
Заметим, что само линейное пространство может рассматриваться как линейная оболочка любого своего базиса.
Пример
4.
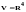 Найти
размерность и базис линейной оболочки
векторов
Найти
размерность и базис линейной оболочки
векторов
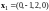 ,
,
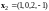 ,
,
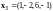 .
.
Найдем
ранг матрицы, строками которой являются
данные векторы
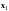 ,
,
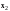 ,
,
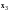 :
:
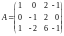 ~
~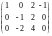 ~
~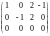 .
.
Минор
второго порядка
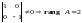 ,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы
и
составляют линейно независимую систему
векторов в
,
следовательно, первые две строки матрицы
линейно независимы. Значит, векторы
и
составляют линейно независимую систему
векторов в
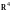 ,
а следовательно, и в линейной оболочке
,
а следовательно, и в линейной оболочке
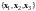 ,
и вектор
через них линейно выражается. Тогда
любой вектор
тоже линейно выражается через
и
.
Векторы
и
являются базисом в
,
и вектор
через них линейно выражается. Тогда
любой вектор
тоже линейно выражается через
и
.
Векторы
и
являются базисом в
 ,
,
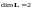 .
.
Упражнение.
-
линейное пространство арифметических
векторов
.
Найти размерность и все
базисы линейной оболочки векторов
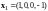 ,
,
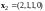 ,
,
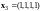 ,
,
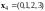 .
.
Лекция 12
Линейные операторы
Линейный оператор - определение и примеры. Матрица линейного оператора. Собственные числа и собственные векторы. Линейные операторы с простым спектром |
12.1. Понятие линейного оператора
Определение
1. Пусть
- линейное пространство и каждому вектору
,
принадлежащему
,
поставлен в соответствие вектор
,
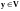 .
Соответствие
.
Соответствие
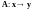 называется оператором,
определенным в линейном пространстве
.
называется оператором,
определенным в линейном пространстве
.
Принята
также запись:
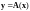 .
Вектор
называется прообразом,
а
- образом
при отображении оператором
.
Вектор
называется прообразом,
а
- образом
при отображении оператором
 .
.
Определение 2. Оператор , определенный в линейном пространстве , называется линейным, если:
1)
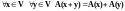 ;
;
2)
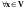
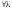 - вещественного числа
- вещественного числа
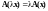 .
.
П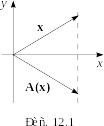 ример
1.
-
линейное пространство всех геометрических
векторов плоскости,
- зеркальное отражение относительно
оси
ример
1.
-
линейное пространство всех геометрических
векторов плоскости,
- зеркальное отражение относительно
оси
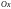 (рис. 12.1).
- линейный оператор.
(рис. 12.1).
- линейный оператор.
Убедимся, что выполняется требование 2) в определении 2.
Пусть
- произвольное вещественное число, по
определению умножения на
для геометрического вектора
вектор
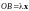 имеет то же направление, что и
,
если
имеет то же направление, что и
,
если
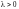 ,
и противоположное, если
,
и противоположное, если
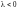 ,
и
,
и
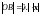 .
.
Рис.
12.2 соответствует случаю
,
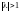 (
рассматривается аналогично).
(
рассматривается аналогично).
П усть
усть
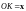 ,
,
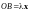 ,
,
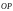 - зеркальное отражение вектора
- зеркальное отражение вектора
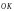 относительно оси
,
относительно оси
,
 - зеркальное отражение вектора
- зеркальное отражение вектора
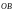 .
Тогда
.
Тогда
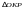 ~
~
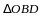 и, значит,
и, значит,
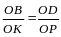 .
Но
.
Но
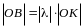 ,
поэтому
,
поэтому
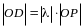 .
Кроме того, направление вектора
.
Кроме того, направление вектора
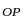 совпадает с направлением вектора
совпадает с направлением вектора
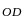 ,
следовательно,
,
следовательно,
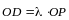 .
Таким образом, имеем
.
Таким образом, имеем
 .
.
Так
же, исходя из геометрических соображений,
можно доказать, что
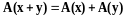 ,
следовательно, оператор
,
следовательно, оператор
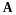 зеркального отражения относительно
оси
зеркального отражения относительно
оси
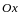 является линейным оператором.
является линейным оператором.
Определение
3.
Пусть
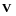 -
линейное пространство,
-
линейное пространство,
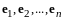 -
базис в
,
-
линейный оператор в
.
Матрицей линейного оператора
в базисе
называется матрица
-
базис в
,
-
линейный оператор в
.
Матрицей линейного оператора
в базисе
называется матрица
 ,
,
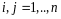 ,
такая,
что
,
такая,
что
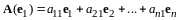 ,
,
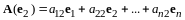 ,
,
…………………………………….. (12.1)
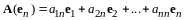 .
.
Замечание
1.
Столбцы матрицы
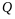 являются координатами в разложении
векторов
являются координатами в разложении
векторов
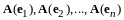 по базису
.
по базису
.
П ример
2.
Найти
матрицу линейного оператора зеркального
отражения относительно оси
в базисе
ример
2.
Найти
матрицу линейного оператора зеркального
отражения относительно оси
в базисе
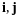 .
.
По
определению оператора
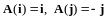 (рис. 12.3).
(рис. 12.3).
Используя
разложение векторов
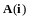 и
и
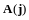 по базису
,
находим:
по базису
,
находим:
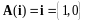 ,
,
 .
Полученные строки координат располагаем
по столбцам:
.
Полученные строки координат располагаем
по столбцам:
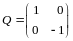 .
.
Упражнение.
 -
линейное пространство всех геометрических
векторов,
-
линейное пространство всех геометрических
векторов,
 - декартов базис,
- декартов базис,
 - декартова система координат,
- оператор проектирования на ось
.
Доказать, что
-
линейный оператор, и найти его матрицу
в базисе
.
- декартова система координат,
- оператор проектирования на ось
.
Доказать, что
-
линейный оператор, и найти его матрицу
в базисе
.
Замечание 2. Пусть - линейное пространство, - линейный оператор в , (I) - базис в . Матрица оператора в базисе (I) определена однозначно.
Для того, чтобы в этом убедиться, разложим векторы по базису (I). Столбцы матрицы представляют собой координаты этих векторов, которые согласно теореме 3 лекции 10 определяются единственным образом, следовательно, матрица оператора в (I) определена однозначно.
Теорема
1.
Пусть
-
линейное пространство,
(I)
- базис в
,
-
линейный оператор в
,
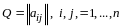 - матрица линейного оператора
в базисе (I),
- матрица линейного оператора
в базисе (I),
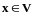 ,
,
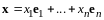 ,
,
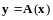 ,
,
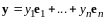 .
Тогда
.
Тогда
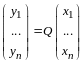 .
.
Доказательство. Имеем
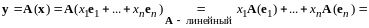
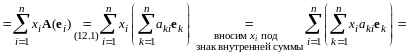
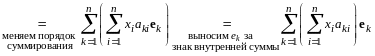 .
.
По
условию
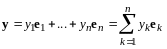 .
.
Используя теорему о единственности разложения вектора по базису (теорема 3 из лекции 10), получим
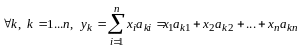 .
(12.2)
.
(12.2)
Заметим,
что в последнем равенстве числа
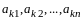 - элементы k-й
строки матрицы
.
- элементы k-й
строки матрицы
.
Привлекая правило умножения матриц, равенство (12.2) запишем в виде
.
Теорема доказана.
Пример 3. Для линейного оператора зеркального отражения относительно оси найти, как преобразуются координаты произвольного вектора.
Решение. Матрица оператора была найдена в примере 2:
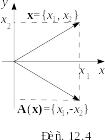 .
.
В
силу теоремы 1, если
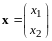 - прообраз, а
- образ,
- прообраз, а
- образ,
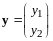 ,
то
,
то
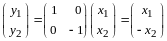 ,
т.е. первая координата образа остается
без изменения, а вторая меняет лишь знак
(рис. 12.4).
,
т.е. первая координата образа остается
без изменения, а вторая меняет лишь знак
(рис. 12.4).
Пример
4.
 -
линейное пространство всех многочленов
степени
-
линейное пространство всех многочленов
степени
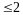 ,
-
линейный оператор дифференцирования.
Найти его матрицу в базисе
,
-
линейный оператор дифференцирования.
Найти его матрицу в базисе
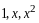 и, используя теорему 1, продифференцировать
многочлен
и, используя теорему 1, продифференцировать
многочлен
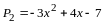 .
.
Решение.
Находим
образы векторов базиса
 и разлагаем полученные векторы по базису
:
и разлагаем полученные векторы по базису
:
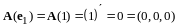 ,
,
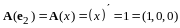 ,
,
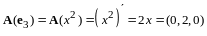 .
.
Матрица оператора в базисе имеет вид
 ,
,
а
вектор
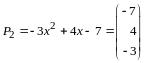 .
Обозначим
.
Обозначим
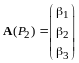 .
По теореме 1 имеем
.
По теореме 1 имеем
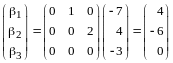 ,
,
или
в виде разложения по базису
:
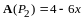 .
.
Упражнение.
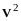 -
линейное пространство всех геометрических
векторов плоскости,
-
линейное пространство всех геометрических
векторов плоскости,
 -
декартов базис,
-
декартов базис,
 -
декартова система координат,
-
оператор поворота плоскости вокруг
начала координат на угол
-
декартова система координат,
-
оператор поворота плоскости вокруг
начала координат на угол
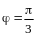 против часовой стрелки. Доказать, что
- линейный оператор, найти матрицу
оператора
в базисе
и координаты образа вектора
против часовой стрелки. Доказать, что
- линейный оператор, найти матрицу
оператора
в базисе
и координаты образа вектора
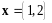 .
.
12.2. Собственные векторы и собственные значения
линейного оператора
Определение
4.
Квадратные
матрицы
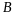 и
и
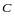 называются подобными,
если существует невырожденная матрица
,
такая,
что
называются подобными,
если существует невырожденная матрица
,
такая,
что
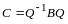 .
.
Теорема
2.
Пусть
- линейное пространство,
(I)
и
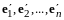 (II)
- два базиса в
,
(II)
- два базиса в
,
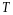 - матрица перехода от (I)
к (II),
- линейный оператор в
,
- матрица оператора
в (I),
- матрица оператора
в (II).
Тогда
- матрица перехода от (I)
к (II),
- линейный оператор в
,
- матрица оператора
в (I),
- матрица оператора
в (II).
Тогда
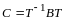 .
.
Это утверждение примем без доказательства.
Пусть
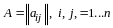 .
Матрица
.
Матрица
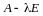 ,
где
,
где
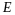 - единичная матрица порядка
- единичная матрица порядка
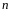 ,
а
,
а
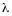 - произвольное вещественное число,
называется характеристической
матрицей для
.
Она имеет вид
- произвольное вещественное число,
называется характеристической
матрицей для
.
Она имеет вид
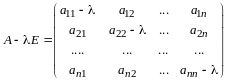 .
.
Определитель
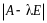 - некоторый многочлен порядка
относительно
.
- некоторый многочлен порядка
относительно
.
Определение 5. Многочлен называется характеристическим многочленом матрицы , а его корни - характеристическими корнями матрицы .
Теорема 3. Подобные матрицы имеют одинаковый набор характеристических корней.
Доказательство. Пусть , - невырожденная матрица. Имеем
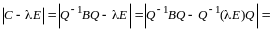
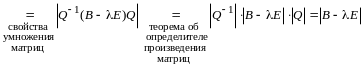 .
.
Характеристические многочлены матриц В и С совпадают, следовательно, совпадают и характеристические корни.
Теорема доказана.
Следствие. Матрицы, задающие линейный оператор в различных базисах, имеют один набор характеристических корней (теорема 2 + теорема 3).
Определение 6. Характеристические корни матрицы линейного оператора (в любом базисе) называются характеристическими корнями линейного оператора.
Определение 7. Весь набор характеристических корней называется спектром оператора.
Определение
8.
Пусть
- линейное пространство,
- линейный оператор в
.
Вектор
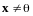 называется собственным вектором
оператора
,
если найдется действительное число
такое, что
называется собственным вектором
оператора
,
если найдется действительное число
такое, что
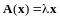 .
.
Число
называется собственным значением,
соответствующим данному собственному
вектору
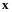 .
.
Справедливо следующее утверждение, которое приведем без доказательства.
Теорема 4. Действительные характеристические корни линейного оператора, если они существуют, и только они, служат собственными значениями линейного оператора.
Пример 5. Найти собственные векторы и собственные значения линейного оператора зеркального отражения относительно оси .
Решение. Матрица оператора была найдена в примере 2: .
Составим характеристическое уравнение:
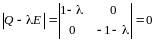 ,
,
откуда
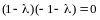 и
и
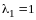 ,
,
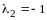 .
.
Числа , - характеристические корни линейного оператора (в соответствии с определением 6), они действительны и, согласно теореме 4, являются собственными значениями. Найдем соответствующие им собственные векторы.
По
определению собственного вектора
,
но
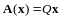 ,
следовательно, ищем векторы, удовлетворяющие
уравнению
,
следовательно, ищем векторы, удовлетворяющие
уравнению
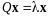 ,
или
,
или
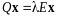 ,
или
,
или
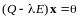 .
(12.3)
.
(12.3)
При
имеем
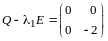 .
Подставим ее в (12.3):
.
Подставим ее в (12.3):
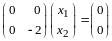 ,
,
что равносильно системе уравнений
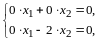 (12.4)
(12.4)
откуда
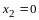 ,
и решением системы (12.4) являются все
векторы вида
,
и решением системы (12.4) являются все
векторы вида
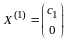 ,
,
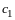 -
произвольное вещественное число,
отличное от нуля.
-
произвольное вещественное число,
отличное от нуля.
При
получаем
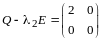 ,
подставляем в (12.3):
,
подставляем в (12.3):
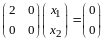 ,
,
получаем систему уравнений
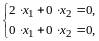
откуда
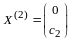 ,
,
 - произвольное вещественное число,
отличное от нуля.
- произвольное вещественное число,
отличное от нуля.
Г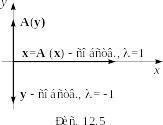 еометрически
это означает, что любой ненулевой вектор,
приложенный к началу координат с концом
на оси
,
является собственным, отвечающим
собственному значению
(действие на него оператора
сводится к умножению его на
,
а любой ненулевой вектор с концом на
оси
еометрически
это означает, что любой ненулевой вектор,
приложенный к началу координат с концом
на оси
,
является собственным, отвечающим
собственному значению
(действие на него оператора
сводится к умножению его на
,
а любой ненулевой вектор с концом на
оси
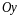 является собственным, отвечающим
собственному значению
(т.е. действие оператора
на этот вектор заключается в умножении
его на
(рис. 12.5)).
является собственным, отвечающим
собственному значению
(т.е. действие оператора
на этот вектор заключается в умножении
его на
(рис. 12.5)).
Упражнение. - линейное пространство всех геометрических векторов, - линейный оператор проектирования на ось . Найти все его собственные числа и собственные векторы.
12.3. Приведение матрицы линейного оператора
к диагональному виду путем перехода к новому базису
Линейный оператор задается в базисе (I) диагональной матрицей тогда и только тогда, когда все векторы базиса (I) - собственные.
Действительно,
пусть
(I)
- собственные векторы, отвечающие
собственным значениям
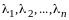 соответственно, т.е.
соответственно, т.е.
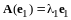 ,
,
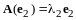 ,
,
………………. (12.5)
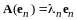 .
.
Из равенств (12.5) следует справедливость разложений по базису (I):
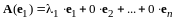 ,
,
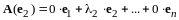 ,
,
…………………………………….
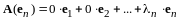 ,
,
и по определению матрицы оператора (определение 3) имеем
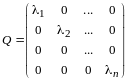 ,
(12.6)
,
(12.6)
т.е. матрица оператора в (I) - диагональная (по диагонали стоят собственные значения).
Обратно.
Пусть
- матрица оператора
в базисе (I)
имеет диагональный вид (12.6), следовательно,
,…,
и, таким образом, векторы
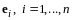 - собственные с собственными значениями
- собственные с собственными значениями
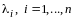 .
.
Вопрос о том, можно ли линейный оператор задать в некотором базисе диагональной матрицей, равносилен вопросу о том, существует ли для данного оператора базис, состоящий из собственных векторов.
Теорема
5.
Пусть
-
линейное пространство,
-
линейный оператор в
,
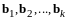 - собственные векторы оператора
,
отвечающие собственным значениям
- собственные векторы оператора
,
отвечающие собственным значениям
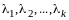 .
Если
.
Если
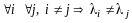 ,
то
- линейно независимы.
,
то
- линейно независимы.
Доказательство.
Доказательство проведем индукцией по
числу векторов
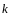 .
.
При
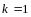 имеем один вектор
имеем один вектор
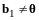 (по определению собственный вектор
отличен от нулевого), вектор
(по определению собственный вектор
отличен от нулевого), вектор
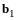 составляет линейно независимую систему.
составляет линейно независимую систему.
Пусть
утверждение теоремы справедливо для
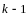 :
всякая система
собственных векторов, отвечающих
различным собственным значениям,
является линейно независимой.
:
всякая система
собственных векторов, отвечающих
различным собственным значениям,
является линейно независимой.
Пусть имеется система собственных векторов , относящихся к различным собственным значениям ( ).
Предположим,
система
линейно зависима, т.е. найдутся числа
 ,
не все равные нулю, такие, что выполняется
равенство
,
не все равные нулю, такие, что выполняется
равенство
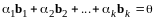 .
(12.7)
.
(12.7)
Не
ограничивая общности рассуждений, можем
считать, что
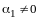 (иначе перенумеруем векторы).
(иначе перенумеруем векторы).
Применим к обеим частям равенства (12.7) оператор :
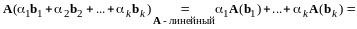
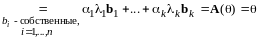 .
.
Из последнего равенства получим
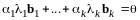 .
(12.8)
.
(12.8)
Обе
части равенства (12.7), умноженные на
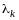 ,
вычтем почленно из обеих частей (12.8),
получим
,
вычтем почленно из обеих частей (12.8),
получим
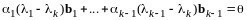 .
(12.9)
.
(12.9)
Равенство
(12.9) означает, что векторы
 линейно зависимы (их линейная комбинация
с коэффициентами, не равными одновременно
нулю, например, коэффициент при
отличен от нуля, равна
линейно зависимы (их линейная комбинация
с коэффициентами, не равными одновременно
нулю, например, коэффициент при
отличен от нуля, равна
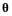 ),
но это противоречит предположению
индукции: векторы
собственные, относящиеся к различным
собственным значениям. Следовательно,
- линейно независимы, и утверждение
теоремы справедливо при любом
.
Теорема доказана.
),
но это противоречит предположению
индукции: векторы
собственные, относящиеся к различным
собственным значениям. Следовательно,
- линейно независимы, и утверждение
теоремы справедливо при любом
.
Теорема доказана.
Определение 9. Линейный оператор называется линейным оператором с простым спектром, если все его характеристические корни действительны и различны.
Теорема 6. Всякий линейный оператор с простым спектром может быть задан диагональной матрицей.
Доказательство.
Пусть
-
линейное пространство,
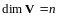 ,
- линейный оператор в
,
имеет простой спектр. Тогда характеристических
корней
.
Пусть это числа
,
в силу теоремы 4
- собственные значения оператора
.
,
- линейный оператор в
,
имеет простой спектр. Тогда характеристических
корней
.
Пусть это числа
,
в силу теоремы 4
- собственные значения оператора
.
Пусть - соответствующие этим собственным значениям собственные векторы, тогда согласно теореме 5 линейно независимы, и так как , - базис. В этом базисе, как было отмечено выше, матрица оператора имеет вид
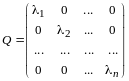
и является диагональной матрицей.
Теорема доказана.
Пример
6.
Линейный оператор
задан своей матрицей
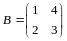 в некотором базисе. Выяснить, существует
ли для данного оператора базис, в котором
его матрица имеет диагональный вид. В
случае положительного ответа найти
этот базис и соответствующую ему матрицу
.
в некотором базисе. Выяснить, существует
ли для данного оператора базис, в котором
его матрица имеет диагональный вид. В
случае положительного ответа найти
этот базис и соответствующую ему матрицу
.
Решение. Составляем и решаем характеристическое уравнение:
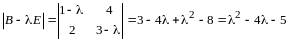 ,
,
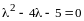 ,
,
откуда
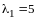 ,
- характеристические корни оператора
.
Они вещественны и различны, следовательно,
согласно теореме 6 для оператора
существует базис, состоящий из собственных
векторов, и в этом базисе матрица
оператора имеет вид
,
- характеристические корни оператора
.
Они вещественны и различны, следовательно,
согласно теореме 6 для оператора
существует базис, состоящий из собственных
векторов, и в этом базисе матрица
оператора имеет вид
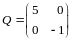 .
.
Находим собственные векторы.
При имеем
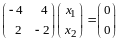 ,
,
или
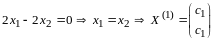 .
Все ненулевые векторы вида
.
Все ненулевые векторы вида
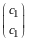 являются собственными с собственным
значением
.
являются собственными с собственным
значением
.
При имеем
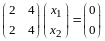 ,
,
или
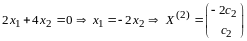 .
Все ненулевые векторы вида
.
Все ненулевые векторы вида
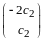 - собственные с собственным значением
.
- собственные с собственным значением
.
Полагаем
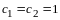 ,
имеем
,
имеем
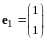 ,
,
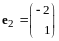 .
.
В
базисе
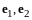 матрица оператора
имеет вид
.
матрица оператора
имеет вид
.
Лекция 13
Евклидовы пространства
-
Определение евклидова пространства.
Ортогональные и ортонормированные базисы.
Процесс ортогонализации Шмидта
13.1. Понятие евклидова пространства
Определение
1.
Евклидовым
пространством
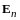 называется n-мерное
линейное пространство, в котором каждой
паре векторов
называется n-мерное
линейное пространство, в котором каждой
паре векторов
 поставлено в соответствие вещественное
число,
называемое скалярным произведением
векторов
и
поставлено в соответствие вещественное
число,
называемое скалярным произведением
векторов
и
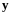 (это
число обозначим
(это
число обозначим
 ),
причем выполняются следующие аксиомы:
),
причем выполняются следующие аксиомы:
1.
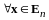
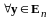
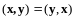 ;
;
2.
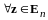
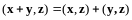 ;
;
3.
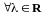
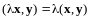 ;
;
4.
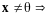
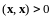 .
.
Замечание.
Аксиомы 2 и 3 справедливы также в форме
2’:
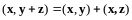 и форме 3’:
и форме 3’:
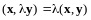 .
.
Пример 1. Пусть - линейное пространство геометрических векторов, скалярное произведение определено равенством
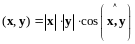 .
(13.1)
.
(13.1)
Аксиомы 1 - 4 выполняются (см. алгебраические свойства скалярного произведения, доказанные в Лекции 2), следовательно, со скалярным произведением, определенным равенством (13.1), является евклидовым пространством.
Пример
2.
В линейном пространстве арифметических
векторов
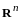 формула
формула
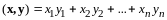 ,
(13.2)
,
(13.2)
где
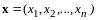 ,
,
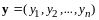 ,
задает скалярное произведение. Докажем
это. Проверим выполнение аксиом 1 - 4.
Поскольку компоненты
,
задает скалярное произведение. Докажем
это. Проверим выполнение аксиом 1 - 4.
Поскольку компоненты
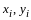
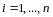 - вещественные числа, имеем
- вещественные числа, имеем
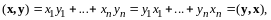
следовательно, аксиома I выполняется.
Пусть
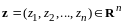 .
По определению сложения в
.
По определению сложения в
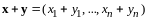 .
Имеем
.
Имеем
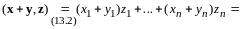
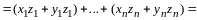
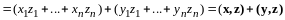 ,
,
аксиома 2 справедлива.
Пусть - произвольное вещественное число. По определению умножения вектора на число в
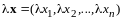 .
.
Далее имеем
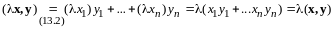 ,
,
аксиома 3 выполняется.
Проверим
выполнение аксиомы 4:
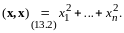
Если
,
то среди компонент вектора
найдется
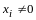 ,
,
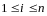 ,
тогда
,
тогда
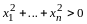 и
и
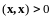 ,
следовательно, аксиома 4 выполняется.
,
следовательно, аксиома 4 выполняется.
Таким образом, линейное пространство арифметических векторов со скалярным произведением (13.2) является евклидовым пространством.
В любом евклидовом пространстве справедливы следствия из аксиом 1 - 4:
а)
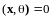 ;
;
б)
если
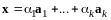 ,
,
 ,
то
,
то
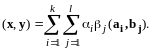
Доказательство следствий проведите самостоятельно.
Определение
2.
Нормой
вектора
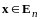 называется число,
равное
называется число,
равное
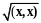 .
.
Обозначим
норму
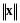 .
Норма
- аналог длины вектора, определенной
для геометрических векторов.
.
Норма
- аналог длины вектора, определенной
для геометрических векторов.
Угол между векторами и в евклидовом пространстве определяется равенством
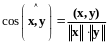 .
(13.3)
.
(13.3)
Покажем,
что угол
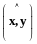 действительно можно определить равенством
(13.3), т.е. покажем, что
действительно можно определить равенством
(13.3), т.е. покажем, что
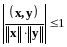 .
.
Теорема
1 (неравенство Коши - Буняковского).
Для
любого
и
любого
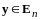 справедливо
неравенство
справедливо
неравенство
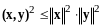 .
(13.4)
.
(13.4)
Доказательство.
Пусть
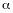 - произвольное вещественное число.
Положим
- произвольное вещественное число.
Положим
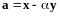 .
Тогда по аксиоме 4 имеем
.
Тогда по аксиоме 4 имеем
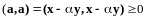 .
.
Воспользуемся аксиомами 1 - 3:
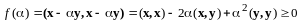 .
.
Так
как
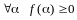 ,
то дискриминант
,
то дискриминант
 квадратного трехчлена
квадратного трехчлена
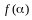 неположителен:
неположителен:
 .
.
Отсюда
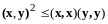 или
,
и неравенство (13.4) выполняется.
или
,
и неравенство (13.4) выполняется.
Теорема доказана.
13.2. Ортогональные и ортонормированные
базисы в
Определение 3. Пусть - евклидово пространство, , . Векторы и называются ортогональными, если
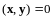 .
.
Определение
4.
Система
векторов
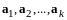 называется ортогональной системой
векторов в евклидовом пространстве
,
если
называется ортогональной системой
векторов в евклидовом пространстве
,
если
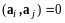 при
при
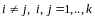 .
.
Справедливо следующее утверждение.
Теорема 2. В евклидовом пространстве всякая система ненулевых ортогональных векторов линейно независима.
Доказательство.
Пусть
- произвольная ортогональная система
векторов в
;
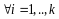
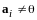 .
.
Пусть
 .
(13.5)
.
(13.5)
Умножим
обе части (13.5) скалярно на
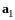 :
:
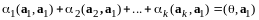 .
(13.6)
.
(13.6)
Поскольку
система векторов
ортогональна, то верны равенства
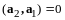 ,…,
,…,
 ;
следствие а) из аксиом дает
;
следствие а) из аксиом дает
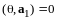 ;
согласно аксиоме 4
;
согласно аксиоме 4
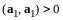 .
Тогда из равенства (13.6) получим
.
Тогда из равенства (13.6) получим
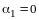 .
.
Аналогично,
скалярно умножая (13.5) последовательно
на
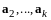 ,
получим
,
получим
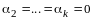 ,
следовательно, система
линейно независима.
,
следовательно, система
линейно независима.
Теорема доказана.
Опишем процесс построения ортогонального базиса в линейной оболочке любых линейно независимых векторов.
Пусть линейно независимы.
Шаг
1.
Примем
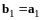 .
.
Шаг
2.
Примем
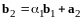 .
Отметим, что
.
Отметим, что
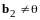 ,
так как
,
так как
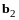 является линейной комбинацией
и
является линейной комбинацией
и
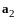 ,
причем
и
линейно независимы (линейная комбинация
векторов
и
с коэффициентами, один из которых, а
именно коэффициент при
,
заведомо отличен от нуля, не может
равняться
,
причем
и
линейно независимы (линейная комбинация
векторов
и
с коэффициентами, один из которых, а
именно коэффициент при
,
заведомо отличен от нуля, не может
равняться
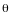 ).
).
Подберем
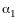 так, чтобы
так, чтобы
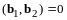 :
:
 и
и
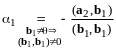 .
.
Шаг
3.
Примем
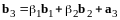 .
Отметим, что
.
Отметим, что
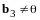 ,
так как
,
так как
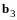 является линейной комбинацией
,
и
является линейной комбинацией
,
и
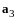 ,
а эти векторы линейно независимы.
Подберем
,
а эти векторы линейно независимы.
Подберем
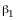 и
и
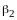 так, чтобы
так, чтобы
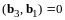 и
и
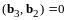 .
.
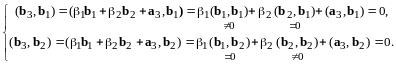
Отсюда
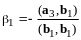 ,
,
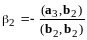 .
.
Шаг
4.
Пусть уже построена ортогональная
система ненулевых векторов
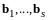 ,
причем
,
причем
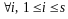 ,
,
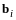 является линейной комбинацией векторов
является линейной комбинацией векторов
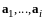 .
Положим
.
Положим
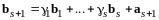 .
.
Вектор
 ,
так как является линейной комбинацией
линейно независимых векторов
,
так как является линейной комбинацией
линейно независимых векторов
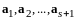 с коэффициентами, один из которых, а
именно коэффициент при
с коэффициентами, один из которых, а
именно коэффициент при
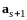 ,
заведомо отличен от нуля (поскольку
не входит в
).
,
заведомо отличен от нуля (поскольку
не входит в
).
Коэффициенты
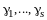 подберем так, чтобы
подберем так, чтобы
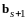 был ортогонален векторам
:
был ортогонален векторам
:
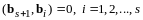 .
.
Отсюда
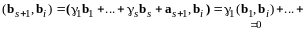
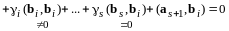
и
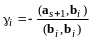 ,
,
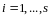 .
.
Продолжая
процесс, построим ортогональную систему
векторов
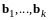 ,
причем
,
причем
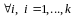 ,
,
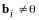 ,
откуда в силу теоремы 2 следует, что
линейно независимы. Линейная оболочка
,
откуда в силу теоремы 2 следует, что
линейно независимы. Линейная оболочка
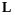 векторов
векторов
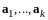 является подпространством размерности
(
является подпространством размерности
(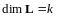 ),
а это означает, что
- базис в
(по построению - ортогональный).
),
а это означает, что
- базис в
(по построению - ортогональный).
Описанный выше процесс носит название процесса ортогонализации Шмидта.
Пример
3.
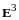 - евклидово пространство геометрических
векторов. Применяя процесс ортогонализации
Шмидта, построить ортогональный базис
в подпространстве, натянутом на векторы
- евклидово пространство геометрических
векторов. Применяя процесс ортогонализации
Шмидта, построить ортогональный базис
в подпространстве, натянутом на векторы
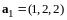 и
и
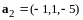 .
.
Полагаем
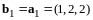 ,
.
,
.
Подбираем :

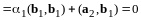 ,
,
о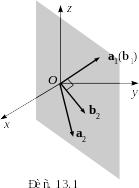 ткуда
ткуда
 .
.
Итак,
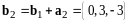 ,
и базис в линейной оболочке
,
и базис в линейной оболочке
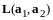 составляют векторы
составляют векторы
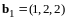 ,
,
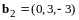 .
.
Геометрический
смысл процедуры иллюстрирует рис. 13.1.
Подпространство
,
натянутое на векторы
 ,
- плоскость, проходящая через
,
- плоскость, проходящая через
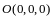 и векторы
и
,
приведенные к точке
.
В этой плоскости построен базис
,
такой, что
и векторы
и
,
приведенные к точке
.
В этой плоскости построен базис
,
такой, что
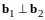 .
.
Замечание. Всякое евклидово пространство обладает ортогональными базисами.
Действительно,
пусть
- евклидово пространство,
 ,
- базис в
.
Применим к базису
процесс ортогонализации Шмидта, получим
некоторый ортогональный базис в
.
,
- базис в
.
Применим к базису
процесс ортогонализации Шмидта, получим
некоторый ортогональный базис в
.
Определение
5.
Вектор
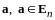 называется нормированным,
если
называется нормированным,
если
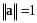 .
.
Если
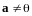 ,
то нормированием
называется переход к вектору
,
то нормированием
называется переход к вектору
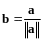 (
(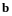 является нормированным, так как
является нормированным, так как
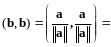
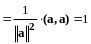 и, следовательно,
и, следовательно,
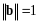 ).
).
Определение
6.
Система
векторов
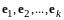 в евклидовом пространстве
называется ортонормированной системой,
если
в евклидовом пространстве
называется ортонормированной системой,
если
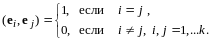
Всякое евклидово пространство обладает ортонормированными базисами.
В
самом деле, ранее было показано, что
всякое евклидово пространство обладает
ортогональными базисами. Возьмем в
произвольный ортогональный базис
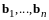 и нормируем все его векторы, т.е. перейдем
к системе векторов
и нормируем все его векторы, т.е. перейдем
к системе векторов
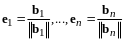 .
(13.7)
.
(13.7)
Система (13.7) - ортонормированный базис в .
Пример 4. - евклидово пространство геометрических векторов. Указать какой-нибудь ортонормированный базис в линейной оболочке векторов и .
В примере 3 был построен ортогональный базис , в .
Имеем
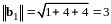 ,
,
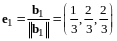 ,
,
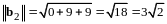 ,
,
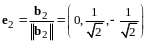 .
.
Векторы - ортонормированный базис в .
Теорема
3.
Пусть
- евклидово пространство,
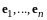 (I)
– базис в
.
Базис
является ортонормированным тогда и
только тогда, когда для любых векторов
,
,
,
скалярное произведение выражается
равенством
(I)
– базис в
.
Базис
является ортонормированным тогда и
только тогда, когда для любых векторов
,
,
,
скалярное произведение выражается
равенством
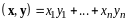 .
.
Доказательство.
Необходимость. Пусть
базис (I)
– ортонормированный, т.е.
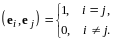
Тогда
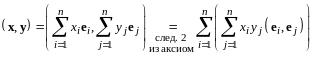 .
.
Но
во внутренней сумме всего одно слагаемое
отлично от нуля при
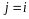 (
( ).
Таким образом,
).
Таким образом,
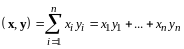 .
.
Достаточность. Пусть базис (I) таков, что , . Для векторов базиса справедливы разложения
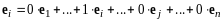 ,
,
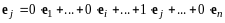 .
.
В
силу этих разложений получим
,
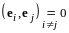 ,
– и базис (I)
– ортонормированный.
,
– и базис (I)
– ортонормированный.
13.3. Линейные операторы в евклидовом пространстве
Определение 7. Квадратная матрица называется ортогональной, если
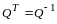 .
.
Пример 5. В линейном пространстве всех геометрических векторов плоскости матрица линейного оператора поворота на угол против часовой стрелки имеет вид
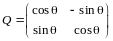 .
.
Для
нее
 ,
и, следовательно,
- ортогональная
матрица.
,
и, следовательно,
- ортогональная
матрица.
Отметим некоторые свойства ортогональной матрицы.
Утверждение 1. Квадратная матрица является ортогональной тогда и только тогда, когда ее столбцы составляют ортонормированную систему арифметических векторов.
Доказательство.
Необходимость.
Пусть
,
 ,
ортогональна.
,
ортогональна.
Имеем
 ,
,
 .
.
В
соответствии с правилом умножения
матриц
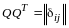 ,
,
где
,
,
где
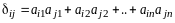 .
(13.8)
.
(13.8)
Так
как
ортогональна, то
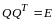 ,
и, следовательно,
,
и, следовательно,
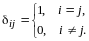 (13.9)
(13.9)
Равенства (13.8) и (13.9) означают, что строки матрицы , рассматриваемые как арифметические n-мерные векторы, составляют ортонормированную систему, необходимость тем самым доказана.
Достаточность. Пусть строки матрицы составляют ортонормированную систему арифметических векторов. Тогда в соответствии с введенными выше обозначениями (см. (13.8))
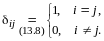
Но
это означает, что
и, следовательно,
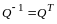 (в силу единственности обратной матрицы)
и
ортогональна.
(в силу единственности обратной матрицы)
и
ортогональна.
Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной.
Доказательство.
Пусть
(I)
и
 (II)
– два ортонормированных базиса в
.
,
,
- матрица перехода от (I)
к (II).
(II)
– два ортонормированных базиса в
.
,
,
- матрица перехода от (I)
к (II).
В соответствии с определением матрицы перехода от базиса к базису справедливо равенство
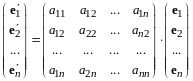 ,
,
или
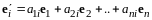 ,
.
(13.10)
,
.
(13.10)
Так
как (II)
– ортонормированный базис, то
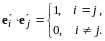
Используя (13.10), получаем
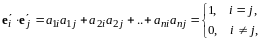
а это означает, что столбцы матрицы составляют ортонормированную систему. Привлекая утверждение I, заключаем, что - ортогональная матрица.
Определение 8. Линейный оператор в евклидовом пространстве называется ортогональным, если
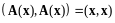
(оператор сохраняет норму любого вектора).
Пример
6.
Евклидово пространство
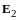 - пространство всех геометрических
векторов плоскости, скалярное произведение
введено равенством
- пространство всех геометрических
векторов плоскости, скалярное произведение
введено равенством
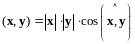 ,
- оператор поворота на угол
,
- оператор поворота на угол
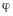 против хода часовой стрелки. Оператор
- ортогональный.
против хода часовой стрелки. Оператор
- ортогональный.
В
самом деле, оператор
- линейный, так как из геометрических
соображений ясно, что
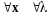 - действительного числа
- действительного числа
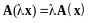 ,
,
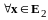
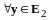
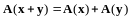 .
А так как при повороте длина любого
вектора сохраняется, то
- ортогональный оператор.
.
А так как при повороте длина любого
вектора сохраняется, то
- ортогональный оператор.
Теорема 4. Пусть - евклидово пространство, - ортогональный оператор в . Тогда
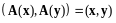
( сохраняет скалярное произведение).
Доказательство.
Пусть
,
,
рассмотрим
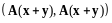 .
.
Имеем

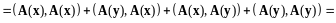
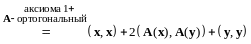 .
(13.11)
.
(13.11)
С другой стороны,
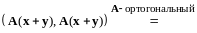
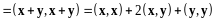 .
(13.12)
.
(13.12)
Сравнивая (13.11) и (13.12) заключаем, что .
Теорема доказана.
Теорема
5.
Пусть
- евклидово пространство,
(I)
- ортонормированный базис,
- ортогональный оператор в
.
Тогда
система
векторов
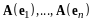 (II)
- ортонормированный базис.
(II)
- ортонормированный базис.
Доказательство. Имеем
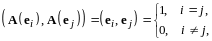
и,
следовательно,
- ортонормированная система. Но тогда
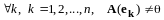 ,
и по теореме 2 система (II)
линейно независима, а так как
,
(II)
– базис, и по доказанному – ортонормированный.
,
и по теореме 2 система (II)
линейно независима, а так как
,
(II)
– базис, и по доказанному – ортонормированный.
Теорема доказана.
Теорема 6. Пусть - евклидово пространство, - ортогональный оператор в . Тогда в любом ортонормированном базисе задается ортогональной матрицей.
Доказательство. Пусть (I) – произвольный ортонормированный базис в . Тогда система векторов (II) – тоже ортонормированный базис (теорема 5).
Пусть - матрица оператора в базисе (I).
В соответствии с определением матрицы оператора (определение 3 в лекции 12) справедливо следующее равенство:

и, следовательно, матрица является матрицей перехода от базиса (I) к базису (II) (см. равенства (11.1) в лекции 11). Тогда в силу доказанного выше утверждения 2 матрица является ортогональной.
Теорема доказана.
Определение 9. Линейный оператор в евклидовом пространстве называется самосопряженным (симметрическим), если
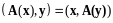 .
.
Пример
7.
Пусть
- произвольное евклидово пространство,
- тождественный оператор, т.е.
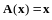 .
.
Имеем
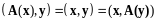 ,
следовательно,
симметрический.
,
следовательно,
симметрический.
Пример 8. Пусть - произвольное евклидово пространство, - некоторое действительное число. Положим .
Справедливо равенство
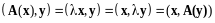 ,
,
и, следовательно, - симметрический.
Отметим некоторые свойства симметрического оператора.
Определение
10.
Матрица
,
,
называется симметрической, если
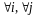
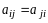 .
.
Теорема 7. Пусть - евклидово пространство, (I) - ортонормированный базис в , - симметрический оператор в . Тогда матрица оператора в (I) симметрическая.
Доказательство. Пусть , - матрица оператора в (I). В соответствии с определением матрицы оператора справедливы следующие равенства:
,
,
…………………………………….. ... (13.13)
.
Воспользовавшись соотношениями (13.13), получим
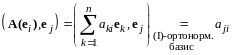 .
(13.14)
.
(13.14)
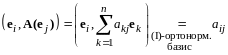 .
(13.15)
.
(13.15)
Так
как
- симметрический оператор,
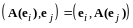 .
.
Сравнивая (13.14) и (13.15), находим, что , и матрица - симметрическая.
Теорема доказана.
Теорема 8. Если линейный оператор , определенный в евклидовом пространстве , задается хотя бы в одном ортонормированном базисе симметрической матрицей, оператор - симметрический.
Доказательство. Пусть - линейный оператор в евклидовом пространстве , (I) – произвольный ортонормированный базис в , , - матрица оператора в базисе (I) (т.е. справедливы равенства (13.13)), - симметрическая, или .
Пусть
,
.
Так как (I)
– базис, найдутся числа
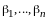 и
и
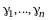 такие, что
такие, что
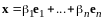 ,
,
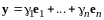 .
.
Имеем
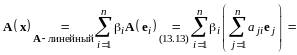
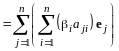 ,
(13.16)
,
(13.16)
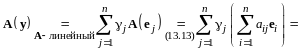
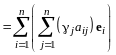 .
(13.17)
.
(13.17)
Используя равенства (13.16) и (13.17) и условие, что (I) – ортонормированный базис, получим
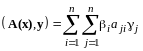 ,
,
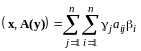 .
.
Так
как
симметрическая,
и
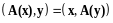 ,
а это означает, что оператор
симметрический.
,
а это означает, что оператор
симметрический.
Теорема доказана.
Приведем без доказательства еще одно свойство самосопряженного оператора.
Теорема 9. Пусть - евклидово пространство, - линейный оператор в . Оператор является симметрическим тогда и только тогда, когда в существует ортонормированный базис, составленный из собственных векторов оператора .
Пример
9.
Линейный оператор
,
определенный в евклидовом пространстве
,
задан в некотором ортонормированном
базисе матрицей
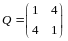 .
Выяснить,
существует ли для этого оператора базис,
в котором его матрица диагональна.
.
Выяснить,
существует ли для этого оператора базис,
в котором его матрица диагональна.
Так как - симметрическая матрица (в ортонормированном базисе), оператор симметрический (теорема 8), а тогда по теореме 9 для него существует базис, состоящий из собственных векторов. В этом базисе матрица оператора диагональна (лекция 12, § 12.3).
Лекция 14
Квадратичные формы
Определение квадратичной формы. Линейное преобразование неизвестных. Ранг формы. Основная теорема о квадратичных формах. Положительно определенные формы. Критерий Сильвестра. Приведение общего уравнения кривой второго порядка к каноническому виду |
14.1. Приведение квадратичной формы
к каноническому виду
Определение 1.
Квадратичной формой от
неизвестных
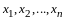 называется сумма вида
называется сумма вида
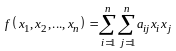 ,
(14.1)
,
(14.1)
или развернуто
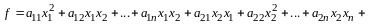
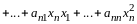 .
(14.2)
.
(14.2)
Матрица
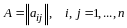 ,
называется матрицей квадратичной
формы (14.1), а ее ранг – рангом формы
(14.1).
,
называется матрицей квадратичной
формы (14.1), а ее ранг – рангом формы
(14.1).
Если ранг формы равен
,
форма называется невырожденной (в
этом случае ранг матрицы
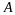 равен
и матрица
невырожденная).
равен
и матрица
невырожденная).
В (14.2)
,
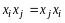 ,
,
поэтому коэффициент при слагаемом
,
,
поэтому коэффициент при слагаемом
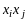 можно обозначить
можно обозначить
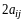 ,
т.е. допустить, что
.
,
т.е. допустить, что
.
Ввиду последнего равенства - симметрическая матрица.
Запишем квадратичную
форму (14.1) в матричном виде. Пусть
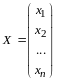 ,
тогда
,
тогда
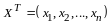 и
и
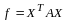 .
(14.3)
.
(14.3)
Действительно, по определению умножения матриц имеем
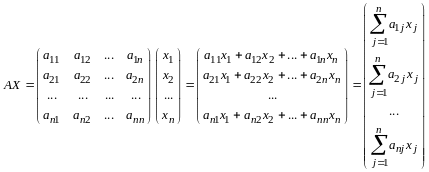 Далее
находим
Далее
находим
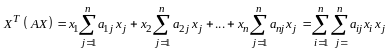
и равенство (14.3) выполняется.
Определение 2. Линейным
преобразованием неизвестных называется
такой переход от системы
неизвестных
к системе
неизвестных
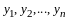 ,
при котором старые неизвестные выражаются
через новые линейно с некоторыми
коэффициентами:
,
при котором старые неизвестные выражаются
через новые линейно с некоторыми
коэффициентами:
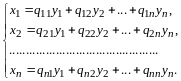 (14.4)
(14.4)
Линейное преобразование
(14.4) однозначно определяется матрицей
из коэффициентов
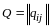 ,
,
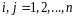 .
.
Систему равенств (14.4) можно записать в матричном виде
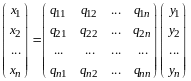 .
(14.5)
.
(14.5)
Определение 3. Линейное преобразование неизвестных с матрицей называется невырожденным, если - невырожденная матрица.
Теорема
1.
Пусть
вслед за линейным преобразованием
(14.4) с матрицей
выполняется
линейное преобразование
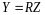 с матрицей
с матрицей
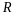 ,
,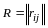 ,
.
Результирующее преобразование будет
линейным с матрицей
,
.
Результирующее преобразование будет
линейным с матрицей
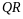 .
.
Доказательство. По условию
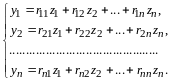 (14.6)
(14.6)
Подставив
в (14.4) выражения для
 ,
,
 ,
из (14.6), получим линейные выражения для
через
,
из (14.6), получим линейные выражения для
через
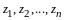 , т.е. результат последовательного
выполнения двух линейных преобразований
неизвестных является линейным
преобразованием.
, т.е. результат последовательного
выполнения двух линейных преобразований
неизвестных является линейным
преобразованием.
Далее
имеем
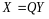 ,
,
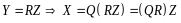 .
Таким образом, результирующее
преобразование имеет матрицей
.
Таким образом, результирующее
преобразование имеет матрицей
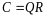 .
.
Пример 1. Вслед за линейным преобразованием
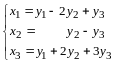
выполняется линейное преобразование
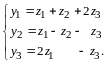
Найти матрицу результирующего
преобразования и выписать выражения
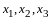 через
через
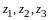 .
.
Решение. Имеем , , где
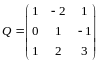 ,
,
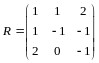 .
.
По теореме 1 матрица результирующего преобразования
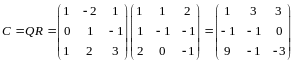 ,
,
и, таким образом,
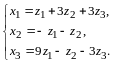
Утверждение 1. Для любых двух матриц А и В
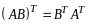 .
.
Доказательство. Пусть
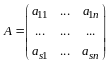 ,
,
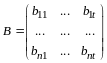 .
.
Обозначим
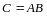 ,
,
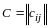 ,
,
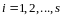 ,
,
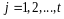 .
По
определению произведения матриц
.
По
определению произведения матриц
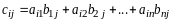 .
.
Обозначим
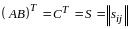 .
По определению транспонированной
матрицы
.
По определению транспонированной
матрицы
 .
.
Обозначим
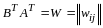 .
Элемент
.
Элемент
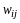 равен сумме произведений элементов
равен сумме произведений элементов
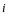 -ой
строки матрицы
-ой
строки матрицы
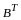 на соответствующие элементы
на соответствующие элементы
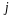 -го
столбца
-го
столбца
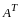 =
сумме произведений элементов
-го
столбца
на соответствующие элементы
-й
строки
,
и приходим к равенству
=
сумме произведений элементов
-го
столбца
на соответствующие элементы
-й
строки
,
и приходим к равенству
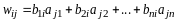 .
.
Таким
образом,
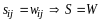 ,
т.е.
.
,
т.е.
.
Теорема
2.
Квадратичная
форма от n
неизвестных с матрицей
после
выполнения линейного преобразования
неизвестных с матрицей
превращается в квадратичную форму от
новых неизвестных с матрицей
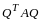 .
.
Доказательство. Пусть
(14.7)
и
,
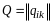 ,
,
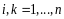 .
.
В
соответствии с утверждением 1
 .
Подставим
.
Подставим
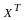 и
и
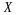 в (14.7):
в (14.7):
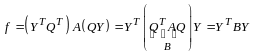 .
.
Матрица симметрическая, так как
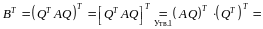
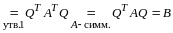 .
.
Таким
образом,
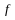 преобразовалась в квадратичную форму
от неизвестных
с матрицей
преобразовалась в квадратичную форму
от неизвестных
с матрицей
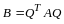 .
.
Докажем два вспомогательных утверждения.
Утверждение 2. Ранг произведения матриц не выше ранга сомножителей.
Доказательство. Достаточно провести доказательство для двух сомножителей.
Пусть
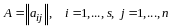 ,
,
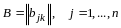 ,
,
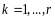 ,
,
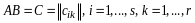 .
.
По определению произведения двух матриц
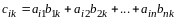 ,
,
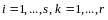 ,
(14.8)
,
(14.8)
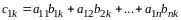 ,
,
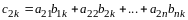 ,
,
……………………………….
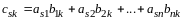 ,
,
или
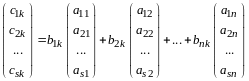 ,
,
т.е.
k-й
столбец матрицы
является линейной комбинацией столбцов
матрицы
с коэффициентами
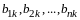 и система столбцов матрицы
линейно выражается через систему
столбцов матрицы
,
следовательно,
и система столбцов матрицы
линейно выражается через систему
столбцов матрицы
,
следовательно,
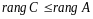 .
.
По определению произведения матриц .
Аналогично,
фиксируя в (14.8)
и придавая
значения
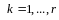 ,
получаем, что
-я
строка
является линейной комбинацией строк
матрицы
и
,
получаем, что
-я
строка
является линейной комбинацией строк
матрицы
и
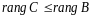 .
.
Утверждение 2 доказано.
Утверждение 3. Ранг произведения произвольной матрицы на невырожденную квадратную матрицу слева или справа равен рангу .
Доказательство.
Пусть
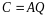 .
В соответствии с утверждением 2
.
.
В соответствии с утверждением 2
.
Умножим
последнее равенство на
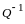 справа:
справа:
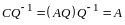 и
опять воспользуемся леммой 2:
и
опять воспользуемся леммой 2:
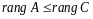 .
Отсюда
.
Отсюда
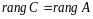 .
.
Следствие из теоремы 2. Ранг квадратичной формы не изменяется при выполнении невырожденного линейного преобразования неизвестных.
Доказательство. Пусть - матрица квадратичной формы , - матрица некоторого невырожденного линейного преобразования неизвестных, - матрица квадратичной формы после выполнения преобразования .
По
теореме 2
,
а в силу утверждения 3
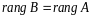 (
(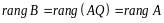 ).
).
Определение 4. Каноническим видом квадратичной формы называют сумму квадратов неизвестных с некоторыми коэффициентами.
Замечание. Число отличных от нуля коэффициентов в каноническом виде квадратичной формы равно рангу формы.
В самом деле, пусть квадратичная форма
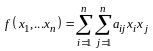 (14.9)
(14.9)
приведена некоторым невырожденным линейным преобразованием неизвестных к каноническому виду
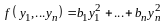 ,
(14.10)
,
(14.10)
где
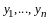 - новые неизвестные.
- новые неизвестные.
Пусть
-
матрица квадратичной формы (14.9),
 ,
,
,
,
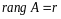 ,
- матрица квадратичной формы (14.10).
,
- матрица квадратичной формы (14.10).
Матрица
имеет следующий вид:
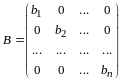 .
.
Согласно следствию из
теоремы 2
 .
Утверждение, что
.
Утверждение, что
 ,
означает, что в матрице
на диагонали ровно
,
означает, что в матрице
на диагонали ровно
 элементов отличны от нуля, тогда в
каноническом виде (14.10) ровно
слагаемых с коэффициентами, отличными
от нуля.
элементов отличны от нуля, тогда в
каноническом виде (14.10) ровно
слагаемых с коэффициентами, отличными
от нуля.
Теорема 3 (основная теорема о квадратичных формах). Всякая квадратичная форма может быть приведена некоторым невырожденным линейным преобразованием к каноническому виду.
Доказательство. Доказательство проведем индукцией по числу неизвестных.
При
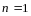 имеем
имеем
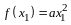 ,
т.е.
- канонического вида.
,
т.е.
- канонического вида.
Пусть
утверждение теоремы справедливо для
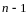 :
всякую квадратичную форму от
неизвестного можно привести к каноническому
виду некоторым невырожденным линейным
преобразованием и пусть
:
всякую квадратичную форму от
неизвестного можно привести к каноническому
виду некоторым невырожденным линейным
преобразованием и пусть
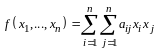 -
-
квадратичная форма от неизвестных .
Случай
1.
В форме
присутствует квадрат хотя бы одного
неизвестного. Не ограничивая общности
рассуждений, можно считать, что
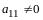 (в противном случае можно заново
перенумеровать неизвестные). Тогда
можно записать в виде
(в противном случае можно заново
перенумеровать неизвестные). Тогда
можно записать в виде
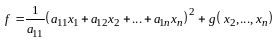 .
(14.11)
.
(14.11)
Действительно,
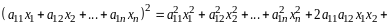
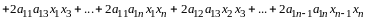 ,
,
и
в первое слагаемое в (14.11) вошли все члены
формы
,
содержащие неизвестное
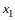 ;
для того, чтобы (14.11) было справедливо,
пришлось добавить, а затем вычесть
несколько слагаемых, не содержащих
,
поэтому в (14.11)
;
для того, чтобы (14.11) было справедливо,
пришлось добавить, а затем вычесть
несколько слагаемых, не содержащих
,
поэтому в (14.11)
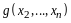 - некоторая квадратичная форма от
неизвестных
- некоторая квадратичная форма от
неизвестных
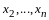 .
.
От
неизвестных
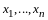 перейдем к
по формулам
перейдем к
по формулам
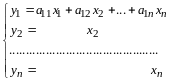 (14.12)
(14.12)
или
в матричной записи:
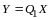 ,
где
,
где
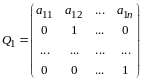 .
.
Матрица
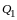 невырожденная, так как
невырожденная, так как
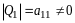 ,
следовательно,
,
следовательно,
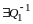 и
и
 .
.
Невырожденное линейное преобразование неизвестных приводит форму к виду
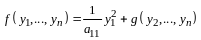 .
(14.13)
.
(14.13)
Квадратичная
форма
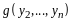 - форма от
- форма от
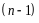 -го
неизвестного и по предположению индукции
найдется невырожденное линейное
преобразование неизвестных
-го
неизвестного и по предположению индукции
найдется невырожденное линейное
преобразование неизвестных
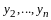 ,
приводящее ее к каноническому виду
,
приводящее ее к каноническому виду
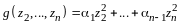 .
Пусть это преобразование с матрицей
,
.
Пусть это преобразование с матрицей
,
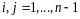 :
:
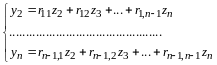
(
- невырожденная матрица и
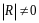 ).
).
Рассмотрим теперь линейное преобразование неизвестных :
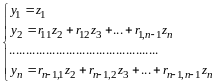 (14.14)
(14.14)
или
в матричной записи
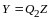 ,
где
,
где
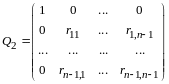 .
.
Линейное
преобразование (14.14) невырожденное, так
как
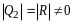 и приводит квадратичную форму (14.13) к
виду
и приводит квадратичную форму (14.13) к
виду
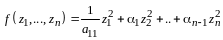 (14.15)
(14.15)
Последовательное
выполнение линейных преобразований
(14.12) и (14.14) является линейным преобразованием
и имеет матрицей
 (теорема 1). Оно будет невырожденным, так
как
(теорема 1). Оно будет невырожденным, так
как
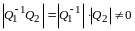 .
Линейное преобразование
.
Линейное преобразование
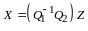 приводит квадратичную форму
приводит квадратичную форму
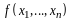 к каноническому виду (14.15).
к каноническому виду (14.15).
Утверждение теоремы в случае 1 доказано.
Случай
2.
Квадратичная форма
не содержит ни одного квадрата неизвестного
(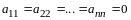 ).
).
Совершим
невырожденное линейное преобразование,
приводящее к появлению квадратов
неизвестных. Пусть, например,
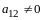 :
:
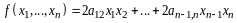 .
(14.16)
.
(14.16)
Положим
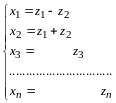
или
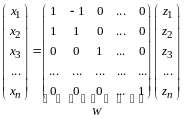 .
.
Линейное
преобразование
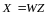 невырожденное, так как
невырожденное, так как
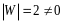 ,
оно приведет квадратичную форму (14.16) к
виду
,
оно приведет квадратичную форму (14.16) к
виду
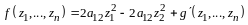 ,
,
появились
квадраты неизвестных
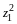 и
и
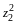 ,
свели к уже рассмотренному случаю 1.
Теорема 3 полностью доказана.
,
свели к уже рассмотренному случаю 1.
Теорема 3 полностью доказана.
Пример 2. Квадратичную форму
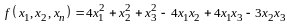
привести к каноническому виду посредством невырожденного линейного преобразования.
Решение. Соберем все слагаемые, содержащие неизвестное , и дополним их до полного квадрата
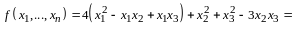
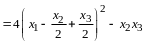 .
.
(Так как
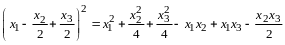 .)
.)
Положим
 (14.17)
(14.17)
и
от неизвестных
 форма
примет вид
форма
примет вид
 .
.
Далее
положим
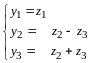 (14.18)
(14.18)
и от неизвестных форма примет уже канонический вид
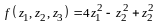 .
(14.19)
.
(14.19)
Разрешим равенства (14.17) относительно :
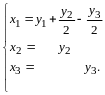
Последовательное
выполнение линейных преобразований
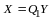 и
,
где
и
,
где
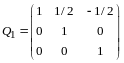 ,
,
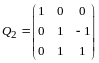 ,
,
имеет матрицей
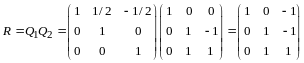 .
.
Линейное
преобразование неизвестных
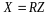 приводит
квадратичную форму
к каноническому виду (14.19).
приводит
квадратичную форму
к каноническому виду (14.19).
14.2. Положительно определенные квадратичные формы
Определение 5.
Нормальным видом квадратичной формы
называется сумма квадратов неизвестных
с коэффициентами «+!» или «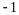 ».
».
Теорема 4. Всякую квадратичную форму можно привести некоторым невырожденным линейным преобразованием неизвестных к нормальному виду.
Доказательство.
Пусть
-
квадратичная форма ранга
.
Следовательно,
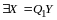 - линейное преобразование неизвестных,
приводящее
к виду
- линейное преобразование неизвестных,
приводящее
к виду
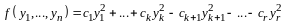 ,
(14.20)
,
(14.20)
где
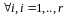 ,
,
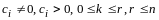 (теорема 3 и следствие из теоремы 2).
(теорема 3 и следствие из теоремы 2).
Положим
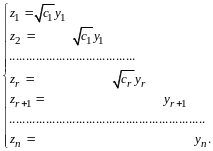 (14.21)
(14.21)
Равенства (14.21) можно записать в виде следующего матричного равенства:
 ,
,
где
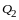 -
невырожденная матрица (так как
-
невырожденная матрица (так как
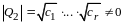 ),
следовательно, существует
),
следовательно, существует
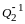 и равенство
и равенство
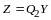 можно разрешить относительно
можно разрешить относительно
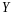 :
:
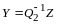 .
.
Последовательное
выполнение линейных преобразований
и
является линейным преобразованием с
матрицей
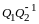 (теорема 1); линейное преобразование
(теорема 1); линейное преобразование
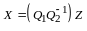 приводит квадратичную форму
к нормальному виду
приводит квадратичную форму
к нормальному виду
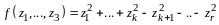 .
.
Теорема 4 доказана.
Определение 6.
Квадратичная форма от n
неизвестных называется положительно
определенной, если она приводится к
нормальному виду, содержащему n
квадратов неизвестных с коэффициентами
«+1»:
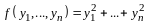
Теорема 5. Квадратичная форма является положительно определенной тогда и только тогда, когда при любых значениях неизвестных, хотя бы одно из которых отлично от нуля, эта форма принимает положительные значения.
Доказательство. Пусть положительно определена, т.е. приводится некоторым невырожденным линейным преобразованием к виду
.
Так
как
- невырожденная матрица,
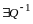 и
и
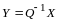 .
Пусть
.
Пусть
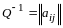 ,
,
тогда
,
,
тогда
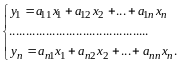 (14.22)
(14.22)
Пусть
-
набор неизвестных, среди которых хотя
бы одно отлично от нуля. Следовательно,
в равенствах (14.22) среди соответствующих
значений
найдется
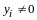 .
Действительно, допустим,
.
Действительно, допустим,

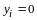 .
Тогда система линейных алгебраических
уравнений
.
Тогда система линейных алгебраических
уравнений
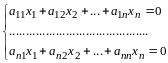
с
определителем
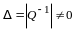 имеет единственное решение
имеет единственное решение
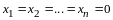 ,
а по условию хотя бы одно из неизвестных
,
а по условию хотя бы одно из неизвестных
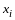 ,
,
отлично от нуля, получили противоречие
и, следовательно, среди
,
,
отлично от нуля, получили противоречие
и, следовательно, среди
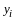 ,
,
есть
.
Тогда
,
,
есть
.
Тогда
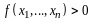 (так как
(так как
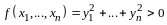 ).
).
Обратно.
Пусть
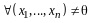 .
Допустим, что
не является положительно определенной,
- это означает, что в нормальном виде, к
которому приводится квадратичная форма
некоторым невырожденным линейным
преобразованием
,
либо отсутствует квадрат хотя бы одного
неизвестного, либо входит с коэффициентом
.
Пусть это неизвестное
.
Допустим, что
не является положительно определенной,
- это означает, что в нормальном виде, к
которому приводится квадратичная форма
некоторым невырожденным линейным
преобразованием
,
либо отсутствует квадрат хотя бы одного
неизвестного, либо входит с коэффициентом
.
Пусть это неизвестное
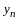 .
Тогда
.
Тогда
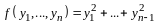 ,
либо
,
либо
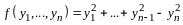 .
.
Рассмотрим следующий набор неизвестных :
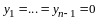 ,
,
 .
(14.23)
.
(14.23)
Пусть неизвестные , , связаны с , , равенствами (14.22). Набор неизвестных , соответствующий (14.23), найдем из системы уравнений
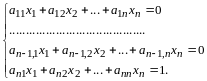 (14.24)
(14.24)
Пусть
- решение системы (14.24), следовательно,
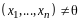 ,
так как если
,
не удовлетворяется, например, последнее
уравнение в (14.24).
,
так как если
,
не удовлетворяется, например, последнее
уравнение в (14.24).
Имеем
и, таким образом,
 ,
получили противоречие, и, значит,
нормальный вид квадратичной формы
содержит
квадратов неизвестных с коэффициентами
+1 и
является положительно определенной
формой.
,
получили противоречие, и, значит,
нормальный вид квадратичной формы
содержит
квадратов неизвестных с коэффициентами
+1 и
является положительно определенной
формой.
Теорема 5 доказана.
Определение 7. Пусть
,
,
.
Миноры
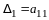 ,
,
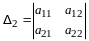 ,
,
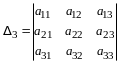 ,
…,
,
…,
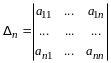 называются главными минорами квадратичной
формы
.
называются главными минорами квадратичной
формы
.
Сформулируем без доказательства следующее утверждение.
Теорема 6 (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все ее главные миноры строго положительны.
Пример
3. Определить,
является ли положительно определенной
квадратичная форма
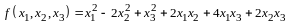 .
.
Решение. Составим матрицу квадратичной формы
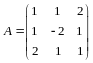
Главные миноры формы
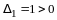 ,
,
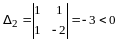 ,
,
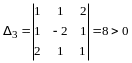 ,
согласно критерию Сильвестра форма не
является положительно определенной.
,
согласно критерию Сильвестра форма не
является положительно определенной.
14.3. Приведение общего уравнения кривой второго порядка к каноническому виду
Пусть на плоскости задана
декартова система координат (декартов
базис
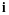 ,
,
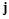 и точка О – начало координат).
Рассмотрим общее уравнение 2-го порядка:
и точка О – начало координат).
Рассмотрим общее уравнение 2-го порядка:
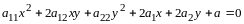 .
(14.25)
.
(14.25)
Обозначим через
 сумму старших слагаемых:
сумму старших слагаемых:
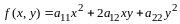
и рассмотрим квадратичную форму
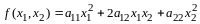 .
.
Ее матрица
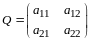 симметрическая.
симметрическая.
Пусть
- произвольное евклидово пространство,
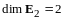 ,
- линейный оператор в
с матрицей
в базисе
,
,
следовательно,
- самосопряженный оператор в
.
Тогда существует ортонормированный
базис, состоящий из собственных векторов
оператора
(см.
лекцию 13, § 13.3, теорема 9), в этом базисе
матрица оператора
диагональная и имеет вид
,
- линейный оператор в
с матрицей
в базисе
,
,
следовательно,
- самосопряженный оператор в
.
Тогда существует ортонормированный
базис, состоящий из собственных векторов
оператора
(см.
лекцию 13, § 13.3, теорема 9), в этом базисе
матрица оператора
диагональная и имеет вид
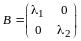 ,
где
,
где
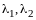 - собственные значения (см. § 12.3).
- собственные значения (см. § 12.3).
Если матрица перехода
от базиса
,
к базису
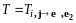 ,
то
,
то
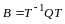 (см.
§ 12.2).
(см.
§ 12.2).
Рассмотрим теперь
линейное преобразование неизвестных
с матрицей
:
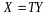 .
Квадратичная форма от новых неизвестных
.
Квадратичная форма от новых неизвестных
 имеет вид
имеет вид
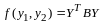 ,
где
,
где
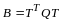 .
.
Итак, если
- ортонормированный базис из собственных
векторов оператора
,
матрица
как матрица перехода от ортонормированного
базиса к ортонормированному ортогональна
(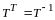 )
, следовательно, матрица квадратичной
формы от неизвестных
диагональная и
)
, следовательно, матрица квадратичной
формы от неизвестных
диагональная и
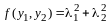 .
.
Такой способ приведения квадратичной формы к каноническому виду называется методом собственных векторов.
Пример
4. Привести
квадратичную форму
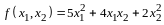 к каноническому виду методом собственных
векторов.
к каноническому виду методом собственных
векторов.
Матрица
квадратичной формы имеет вид
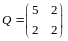 .
Рассмотрим в произвольном евклидовом
пространстве
,
,
линейный оператор
с матрицей
в некотором ортонормированном базисе
.
Найдем его собственные векторы.
.
Рассмотрим в произвольном евклидовом
пространстве
,
,
линейный оператор
с матрицей
в некотором ортонормированном базисе
.
Найдем его собственные векторы.
Характеристическое
уравнение
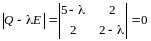 ,
,
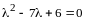 ,
его корни
,
его корни
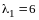 ,
,
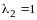 .
.
Имеем для
:
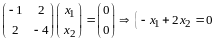 и
и
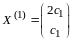 ,
,
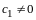 ;
;
для
:
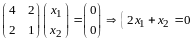 и
и
 ,
,
 .
.
Положим
 ,
,
 и получим
и получим
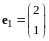 ,
,
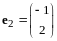 .
.
В базисе
 ,
,
 матрица оператора
диагональная:
матрица оператора
диагональная:
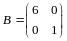 .
Нормируем векторы
и
:
.
Нормируем векторы
и
:
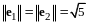 и
и
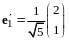 ,
,
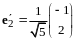 .
.
Матрица перехода от
базиса
,
к базису
 ,
,
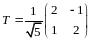 .
Вернемся к квадратичной форме. Положим
,
т.е.
.
Вернемся к квадратичной форме. Положим
,
т.е.
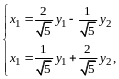 (14.26)
(14.26)
Тогда
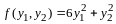 .
.
Замечание. Формулы (14.26) – формулы поворота осей координат на угол против хода часовой стрелки. Угол определяется соотношениями
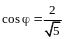 ,
,
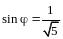 (
(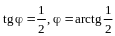 ).
).
В общем случае преобразование поворота
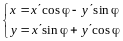 (14.27)
(14.27)
приведет линию (14.25) к виду
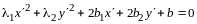 .
(14.28)
.
(14.28)
Эта процедура называется
приведением линии 2-го порядка к главным
осям (из дальнейшего изложения будет
ясно, что, если (14.25) – эллипс или гипербола,
новые оси
 и
и
 параллельны главным осям кривой).
параллельны главным осям кривой).
Коэффициенты
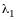 и
и
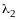 в уравнении (14.28) – характеристические
числа матрицы
и могут быть найдены как корни уравнения
в уравнении (14.28) – характеристические
числа матрицы
и могут быть найдены как корни уравнения
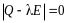 , или
, или
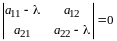 .
(14.29)
.
(14.29)
Обозначим
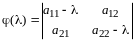 ,
,
 .
.
Имеем
 (действительно, из (14.29) находим
(действительно, из (14.29) находим
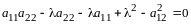 ,
или
,
или
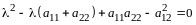 ,
и по теореме Виета
,
и по теореме Виета
 ).
).
Случай
1.
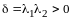 (кривая эллиптического типа).
(кривая эллиптического типа).
Преобразуем (14.28) следующим образом:
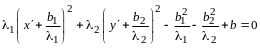 ,
,
или, обозначив
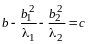 ,
придем к равенству
,
придем к равенству
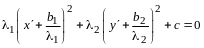 .
.
Положим
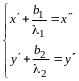 (14.30)
(14.30)
и в новой системе координат
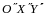 имеем
имеем
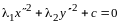 .
(14.31)
.
(14.31)
Формулы (14.30) – формулы
параллельного переноса начала координат
в точку
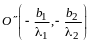 .
.
Случай
1. а) Знак
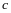 противоположен знаку
(и, следовательно, знаку
).
Тогда (14.31) определяет эллипс:
противоположен знаку
(и, следовательно, знаку
).
Тогда (14.31) определяет эллипс:
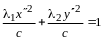 ;
;
б)
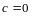 ,
уравнение (14.31) определяет одну точку:
,
уравнение (14.31) определяет одну точку:
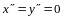 ;
;
в) Знаки и совпадают, нет точек (мнимый эллипс).
Случай
2.
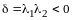 (кривая гиперболического типа).
(кривая гиперболического типа).
В этом случае знаки и противоположны.
а)
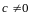 ,
уравнение (14.31) определяет гиперболу:
,
уравнение (14.31) определяет гиперболу:
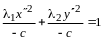 ;
;
б) , уравнение (14.31) принимает вид:
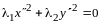 .
.
Пусть
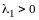 ,
тогда
,
тогда
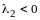 и уравнение (14.31) можно переписать в
следующем виде:
и уравнение (14.31) можно переписать в
следующем виде:
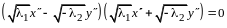 .
(14.32)
.
(14.32)
Уравнение (14.32) определяет
пару пересекающихся прямых:
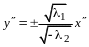 .
.
Случай
3.
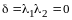 (кривая параболического типа).
(кривая параболического типа).
Пусть для определенности
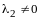 (тогда
(тогда
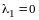 ).
).
Уравнение (14.25) преобразованием (14.27) приводится к виду
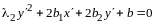 .
(14.33)
.
(14.33)
Пусть
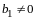 ,
тогда (14.33) можно переписать следующим
образом:
,
тогда (14.33) можно переписать следующим
образом:
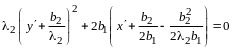 .
.
Получим
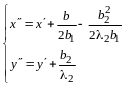 и
и
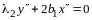 .
(14.34)
.
(14.34)
Уравнение (14.34) определяет параболу.
Если же
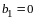 ,
то уравнение (14.33) перепишем в виде
,
то уравнение (14.33) перепишем в виде
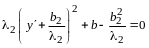 .
.
Обозначив
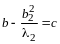 и положив
и положив
 ,
придем к уравнению
,
придем к уравнению
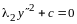 .
(14.35)
.
(14.35)
а)
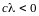 ,
уравнение (14.35) определяет пару параллельных
прямых:
,
уравнение (14.35) определяет пару параллельных
прямых:
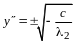 .
.
б)
,
уравнение (14.35) определяет пару совпадающих
прямых:
 .
.
в)
 ,
нет точек (пара мнимых прямых).
,
нет точек (пара мнимых прямых).
Сведем полученные результаты в таблицу:
Кривая эллиптического типа |
и разных знаков |
Эллипс |
|
и одного знака |
Мнимый эллипс |
||
|
Точка |
||
Кривая гиперболического типа |
|
Гипербола |
|
|
Пара пересекающихся прямых |
||
Кривая параболического типа |
|
и одного знака |
Пара мнимых параллельных прямых |
и разных знаков |
Пара параллельных прямых |
||
|
Пара совпадающих прямых |
||
|
|
Парабола |
|
Пример 5. Определить вид и расположение кривой 2-го порядка
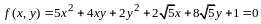 .
(14.36)
.
(14.36)
Слагаемые 2-го порядка в (14.36) составляют квадратичную форму
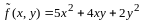 ,
,
которую преобразование неизвестных по формулам
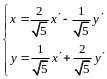 (14.37)
(14.37)
приводит к сумме квадратов
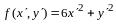 (пример 4).
(пример 4).
Тогда уравнение кривой (14.36) преобразованием (14.37) приводится к виду
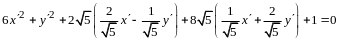 .
.
Здесь
,
и, следовательно,
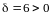 ,
кривая эллиптического типа.
,
кривая эллиптического типа.
Как в случае 1, соберем
слагаемые, содержащие неизвестное
 и дополним их до полного квадрата,
аналогично поступим со слагаемыми,
содержащими
и дополним их до полного квадрата,
аналогично поступим со слагаемыми,
содержащими
 :
:
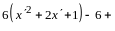
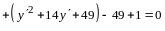 ,
или
,
или
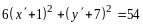
Положим
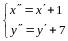 и получим
и получим
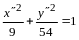
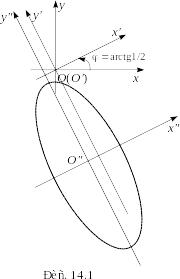 .
(14.38)
.
(14.38)
Уравнение (14.38) – уравнение
эллипса с полуосями
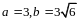 и центром в точке
и центром в точке
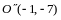 .
Рис. 14.1 - схематический рисунок кривой.
.
Рис. 14.1 - схематический рисунок кривой.