Лекция 6

Матрицы

Определение и некоторые свойства определителей порядка n. Сложение матриц, умножение матрицы на число, умножение матриц. Свойства этих операций

6.1. Основные понятия

Определение 1. Матрицей называется прямоугольная таблица чисел.

Для обозначения матрицы используются круглые скобки или сдвоенные вертикальные линии:

.

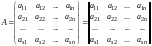Числа, составляющие матрицу, называются ее элементами, элемент 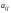матрицы расположен в ее -й строке и -м столбце.

Числа и (число строк и столбцов матрицы) называются ее порядками.

Говорят также, что - матрица размером .

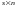Если 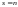, матрица называется квадратной.

Для краткой записи используется также обозначение 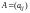(или 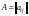) и далее указывается, в каких пределах изменяются и , например, , , 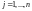. (Запись читается так: матрица с элементами , изменяется от до , - от до .)

Среди квадратных матриц отметим диагональные матрицы, у которых все элементы с неравными индексами ( ) равны нулю:

.

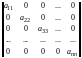Будем говорить, что элементы расположены на главной диагонали.

Диагональная матрица вида

называется единичной матрицей.

В дальнейшем будут встречаться матрицы вида

и ,

которые называются треугольными матрицами, а также матрицы, состоящие из одного столбца:

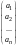
и одной строки:

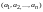
(матрица-столбец и матрица-строка).

Матрица, все элементы которой равны нулю, называется нулевой.

6.2. Определители порядка n

Пусть дана квадратная матрица порядка :

. (6.1)

Составим всевозможные произведения элементов матрицы, расположенных в разных строках и разных столбцах, т.е. произведения вида

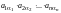. (6.2)

Число произведений вида (6.2) равно (примем этот факт без доказательства).

Будем считать все эти произведения членами определителя порядка , соответствующего матрице (6.1).

Вторые индексы множителей в (6.2) составляют перестановку первых натуральных чисел .

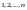Говорят, что числа и в перестановке составляют инверсию, если 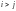, а в перестановке расположено раньше .

Пример 1. В перестановке шести чисел, 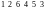, числа и , и , и , и , и составляют инверсии.

Перестановка называется четной, если число инверсий в ней четно, и нечетной, если число инверсий в ней нечетно.

Пример 2. Перестановка - нечетная, а перестановка 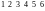- четная ( инверсий).

Определение 2. Определителем порядка , соответствующим матрице (6.1), называется алгебраическая сумма членов, составленная следующим образом: членами определителя служат всевозможные произведения элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем слагаемое берется со знаком "+", если множество вторых индексов является четной перестановкой чисел , и со знаком "–", если нечетной.

Обозначать определитель матрицы (6.1) принято так:

.

Замечание. Определение 2 для 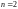и 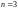приводит к уже знакомым нам определителям 2-го и 3-го порядка:

,

.

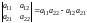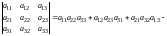
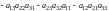Транспонированием вокруг главной диагонали матрицы называется переход к матрице 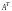, для которой строки матрицы являются столбцами, а столбцы - строками:

.

Будем говорить, что определитель получен транспонированием определителя .

Свойства определителя порядка п:

1. 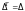(определитель не меняется при транспонировании вокруг главной диагонали).

2. Если одна из строк определителя состоит из нулей, определитель равен нулю.

3. От перестановки двух строк определитель меняет лишь знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на число 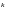, определитель умножится на .

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы -й строки определителя представлены в виде суммы 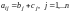, то определитель равен сумме двух определителей, у которых все строки, кроме -й, такие же, как в исходном определителе, а -я строка в одном определителе состоит из 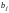, а в другом - из .

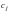Определение 3. -я строка определителя называется линейной комбинацией остальных его строк, если 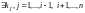такие, что, умножая -ю строку на 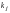, а затем складывая все строки, кроме -й, получаем -ю строку.

8. Если одна из строк определителя является линейной комбинацией остальных его строк, определитель равен нулю.

9. Определитель не изменится, если к элементам одной его строки прибавить соответствующие элементы другой, умноженные на одно и то же число.

Замечание. Мы сформулировали свойства определителя для строк. В силу свойства 1 ( ) они справедливы и для столбцов.

Все приведенные свойства были доказаны на практических занятиях для ; для произвольного примем их без доказательства.

Если в определителе порядка выбрать элемент и вычеркнуть столбец и строку, на пересечении которых расположен , оставшиеся строки и столбцы образуют определитель порядка 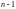, который называется минором определителя , соответствующим элементу .

Пример 3. В определителе

минором элемента 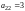является определитель .

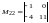Определение 4. Алгебраическим дополнением 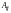элемента определителя называется его минор, умноженный на 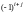, где - номер строки, - номер столбца, в которых расположен выбранный элемент .

Пример 4. В определителе

алгебраическое дополнение .

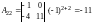Теорема 1 (о разложении по строке). Определитель равен сумме произведений всех элементов любой строки на их алгебраические дополнения.

Теорема 1 позволяет свести вычисление определителя порядка к вычислению определителей порядка .

Пример 5. Вычислить определитель четвертого порядка:

.

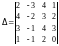Воспользуемся теоремой 1 и разложим определитель по 4-й строке:

.

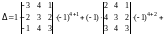
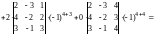
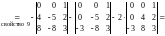
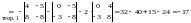Замечание. Можно вначале упростить определитель, воспользовавшись свойством 9, а затем использовать теорему 1. Тогда вычисление определителя порядка сведется к вычислению всего одного определителя порядка .

Пример 6. Вычислить

.

Прибавим первый столбец ко второму и первый столбец, умноженный на (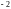 ), к третьему, в результате получим

.

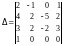Теперь применим теорему 1 и разложим по последней строке:

,

вычисление определителя 4-го порядка свелось к вычислению всего одного определителя 3-го порядка.

Далее аналогично к первому столбцу прибавим третий и полученный определитель разложим по первой строке:

,

вычисление определителя третьего порядка свелось к вычислению всего одного определителя второго порядка.

Пример 7. Вычислить определитель порядка :

.

Первую строку прибавим ко второй, третьей и т.д. -й строке. Придем к определителю

.

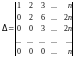Получен определитель треугольного вида.

Применим раз теорему 1 (разложим по первому столбцу) и получим

.

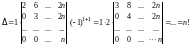Замечание. Определитель треугольного вида равен произведению элементов главной диагонали.

6.3. Основные операции над матрицами

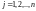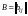Определение 5. Две матрицы , , , и , , , будем называть равными, если .

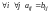Краткая запись: .

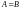Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.

Определение 6. Суммой двух матриц , , , и , , , называется такая матрица 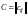, , , что .

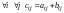Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.

Пример 8. Найти сумму матриц

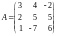и .

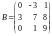В соответствии с определением 6 найдем

.

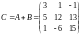Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.

Определение 7. Произведением матрицы , , , на вещественное число называется такая матрица , , , для которой .

Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.

Пример 9. Найти линейную комбинацию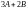 матриц

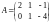и .

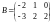Пользуясь определением 7, получаем

, ,

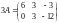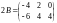далее привлекаем определение суммы матриц (определение 6):

.
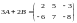