
Свойства операций сложения матриц и умножения на число:
1. Сложение
коммутативно:
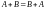 .
.
2. Сложение
ассоциативно: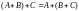 .
.
3. Существует
нулевая матрица
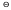 ,
удовлетворяющая условию
,
удовлетворяющая условию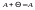 для всех А.
для всех А.
4. Для любой матрицы
А существует противоположная матрица
В, удовлетворяющая условию
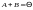 .
.
Для любых матриц
А и В и любых действительных
чисел
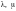 имеют место равенства:
имеют место равенства:
5.
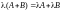 .
.
6.
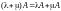 .
.
7.
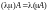 .
.
8.
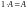 .
.
Проверим свойство
1. Обозначим
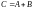 ,
,
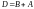 .
Пусть
,
.
Пусть
,
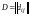 ,
.
Имеем
,
.
Имеем
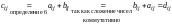 ,
,
и так как равенство
доказано для произвольного элемента,
в соответствии с определением 5
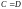 .
Свойство 1 доказано.
.
Свойство 1 доказано.
Аналогично доказывается свойство 2.
В качестве матрицы
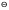 возьмем матрицу порядка
,
все элементы которой равны нулю.
возьмем матрицу порядка
,
все элементы которой равны нулю.
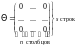
Сложив с любой матрицей по правилу, данному в определении 6, мы матрицу не изменим, и свойство 3 справедливо.
Проверим свойство
4. Пусть
 .
Положим
.
Положим
 .
Тогда
,
следовательно, свойство 4 справедливо.
.
Тогда
,
следовательно, свойство 4 справедливо.
Проверку свойств 5 - 8 опустим.
Определение 8.
Произведением матрицы
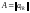 ,
,
,
,
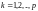 ,
на матрицу
,
на матрицу
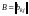 ,
,
,
называется матрица
,
,
,
с элементами
,
,
,
называется матрица
,
,
,
с элементами
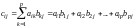 .
.
Краткая запись:
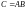 .
.
Пример 10. Найти произведение матриц
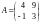 и
и
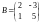 .
.
В соответствии с определением 8 найдем
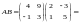
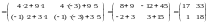 .
.
Пример 11. Перемножить матрицы
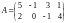 и
и
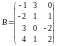 .
.
Имеем
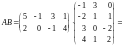
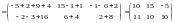 .
.
Замечание
1. Число элементов в строке
матрицы
равно числу элементов в столбце матрицы
 (число столбцов матрицы
равно числу строк матрицы
).
(число столбцов матрицы
равно числу строк матрицы
).
Замечание
2. В матрице
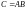 строк столько же, сколько в матрице
,
а столбцов столько же, сколько в
.
строк столько же, сколько в матрице
,
а столбцов столько же, сколько в
.
Замечание
3. Вообще говоря,
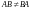 (умножение матриц некоммутативно).
(умножение матриц некоммутативно).
Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.
Пример 12. Перемножим в обратном порядке матрицы и из примера 10.
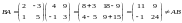 ,
,
таким образом, в общем случае .
Отметим, что в
частном случае равенство
 возможно.
возможно.
Матрицы и , для которых выполняется равенство , называются перестановочными, или коммутирующими.
Свойства умножения матриц:
Умножение дистрибутивно:
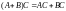 ,
,
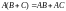 .
.
2. Умножение
ассоциативно:
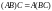 .
.
Докажем свойство
1. Пусть
,
,
,
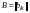 ,
,
,
,
,
,
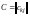 ,
,
.
,
,
.
Обозначим
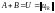 ,
,
,
,
,
,
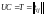 ,
,
,
,
,
,
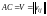 ,
,
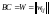 .
.
Имеем
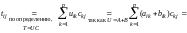
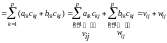 ,
,
и, таким образом,
в соответствии с определением 6
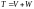 ,
или, возвращаясь к старым обозначениям,
.
Свойство 1 доказано.
,
или, возвращаясь к старым обозначениям,
.
Свойство 1 доказано.
Так как умножение матриц некоммутативно, следовало бы доказать и правую дистрибутивность: . Опустим доказательство, так как оно аналогично приведенному доказательству левой дистрибутивности.
Докажем свойство
2. Пусть
,
,
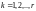 ,
,
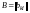 ,
,
,
,
 ,
,
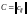 ,
,
.
,
,
.
Обозначим
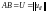 ,
,
,
,
,
,
,
,
,
,
,
,
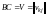 ,
,
,
,
,
,
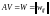 ,
,
.
,
,
.
Имеем
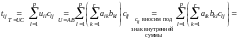
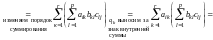
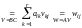 ,
,
таким образом,
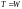 .
.
Вернемся к старым обозначениям и получим: , т.е. свойство 2 доказано.
Для квадратных матриц справедливо следующее утверждение, которое приведем без доказательства.
Теорема 2. Для любых двух квадратных матриц и
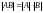 .
.
Приведем пример, иллюстрирующий утверждение теоремы 2.
Пример 13. Даны матрицы
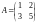 и
и
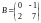 .
.
Вычислить
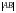 .
.
Воспользуемся
теоремой 2:
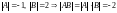 .
.
Найдем произведение
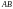 непосредственно:
непосредственно:
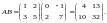
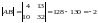 .
Следовательно, результаты совпадают.
.
Следовательно, результаты совпадают.
Лекция 7
Обратная матрица. Ранг матрицы
Построение обратной матрицы методом присоединенной. Ранг матрицы. Нахождение ранга матрицы методами окаймляющих миноров и элементарных преобразований |
7.1. Обратная матрица
Далее будут рассматриваться квадратные матрицы.
Единичная матрица
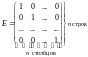
в умножении квадратных матриц порядка играет роль, аналогичную роли числа единица в умножении чисел:
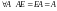 .
(7.1)
.
(7.1)
Действительно, пусть
.
Непосредственная
проверка дает:
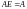 .
Аналогично
.
Аналогично
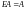 ,
и равенство (7.1) справедливо.
,
и равенство (7.1) справедливо.
Утверждение
1. Матрица
 - единственная матрица, обладающая
свойством (7.1).
- единственная матрица, обладающая
свойством (7.1).
Доказательство.
Пусть
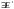 такая, что
такая, что
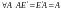 .
(7.2)
.
(7.2)
Рассмотрим
произведение
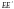 :
:
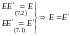 .
.
Определение 1.
Пусть
- произвольная квадратная матрица.
Матрица
называется правой обратной для
,
если
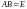 .
Матрица
.
Матрица
 называется левой обратной для
,
если
называется левой обратной для
,
если
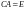 .
.
Определение 2.
Квадратная матрица
называется вырожденной (особенной),
если
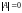 ,
и невырожденной (неособенной), если
,
и невырожденной (неособенной), если
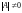 .
.
Утверждение 2. Вырожденная матрица не имеет ни правой, ни левой обратной.
Доказательство. Пусть - вырожденная. Допустим, - правая обратная для , т.е. .
Тогда
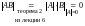 ,
но
,
но
 ,
что является противоречием, следовательно,
не имеет правой обратной.
,
что является противоречием, следовательно,
не имеет правой обратной.
Аналогично доказывается, что не имеет и левой обратной.
Утверждение 3. Пусть - произвольный определитель порядка . Сумма произведений всех элементов любого столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.
Доказательство. Пусть
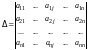 .
.
В силу теоремы о разложении по строке (лекция 6, теорема 1) имеем
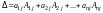 ,
,
где
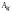 - алгебраическое дополнение к элементу
- алгебраическое дополнение к элементу
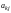 .
.
Пусть
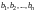 - произвольные вещественные числа.
Рассмотрим сумму
- произвольные вещественные числа.
Рассмотрим сумму
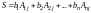 .
.
Привлекая ту же теорему о разложении по строке, можем записать
 .
.
Возьмем в качестве
чисел
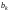 ,
,
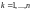 ,
элементы
-го
столбца определителя
,
,
тогда
,
элементы
-го
столбца определителя
,
,
тогда
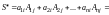

Утверждение 3 доказано.
Перейдем к построению обратной матрицы методом присоединенной. Пусть - невырожденная матрица порядка :
.
Матрица
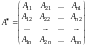
называется
присоединенной для
.
Элементами матрицы
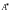 являются алгебраические дополнения к
элементам матрицы
,
причем алгебраические дополнения к
элементам i-й строки
матрицы
помещены в i-й столбец
.
являются алгебраические дополнения к
элементам матрицы
,
причем алгебраические дополнения к
элементам i-й строки
матрицы
помещены в i-й столбец
.
Обозначим
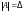 .
.
Матрица
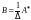 является правой и левой обратной для
.
является правой и левой обратной для
.
Действительно,
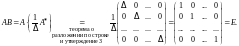
Следовательно,
матрица
- правая обратная для
.
Аналогично
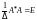 ,
и матрица
является и левой обратной для
.
Она называется обратной для
и обозначается
,
и матрица
является и левой обратной для
.
Она называется обратной для
и обозначается
 .
.
Итак,
 .
.
Утверждение 4. Матрица - единственная обратная для .
Действительно,
допустим,
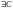 такая, что
такая, что
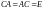 .
.
Рассмотрим
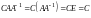 .
С другой стороны,
.
С другой стороны,
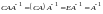 ,
следовательно,
,
следовательно,
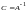 .
.
Пример
1. Найти
для матрицы
 .
.
Решение.
Имеем
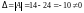 ,
следовательно,
существует.
,
следовательно,
существует.
Найдем алгебраические дополнения к элементам матрицы и составим присоединенную матрицу:
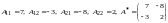 .
.
Откуда
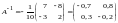 .
.
Пример 2. Решить матричное уравнение
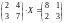 .
.
Решение.
Обозначим
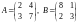 .
Тогда исходное уравнение примет вид
.
Тогда исходное уравнение примет вид
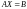 .
(7.3)
.
(7.3)
Имеем
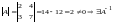 .
.
Домножим обе части уравнения (7.3) слева на матрицу и получим
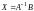 .
.
Итак,
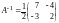 ,
,
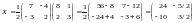 .
.
7.2. Ранг матрицы
Пусть - прямоугольная матрица размера :
.
Назовем арифметическими
-мерными
векторами упорядоченные наборы
чисел, строки матрицы
,
и обозначим их через
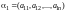 ,
,
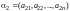 ,…,
,…,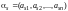 .
.
Нулевым арифметическим
вектором назовем
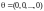 .
.
Будем говорить,
что система векторов
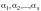 линейно зависима, если
линейно зависима, если
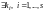 ,
не все равные нулю, что
,
не все равные нулю, что
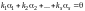 .
.
Система векторов называется линейно независимой, если она не является линейно зависимой.
Пример 3. В матрице
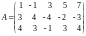
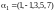 ,
,
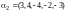 ,
,
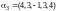 .
.
Имеем
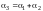 ,
следовательно,
,
следовательно,
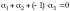 и система строк матрицы
линейно зависима.
и система строк матрицы
линейно зависима.
Заметим, что и столбцы матрицы можно рассматривать как арифметические -мерные векторы.
Определение 3.
Пусть
- прямоугольная матрица размера
.
Выберем в
произвольные
строк и
столбцов.
Элементы, стоящие на пересечении
выбранных строк и столбцов, образуют
определитель
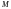 порядка
,
который называется минором порядка
матрицы
.
порядка
,
который называется минором порядка
матрицы
.
Определение 4. Наивысший порядок отличных от нуля миноров матрицы называется рангом матрицы .
Обозначение ранга
:
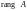 .
.
Пример 4. Найти ранг матрицы :
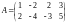 .
.
Решение.
Заметим, что миноры первого порядка -
это элементы матрицы. Выпишем их все (в
данном случае, миноров первого порядка
восемь):
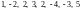 .
.
Уже на этом шаге
можно утверждать, что
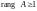 ,
так как среди миноров 1-го порядка есть
отличные от нуля.
,
так как среди миноров 1-го порядка есть
отличные от нуля.
Выпишем все миноры 2-го порядка:
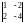 ,
,
 ,
,
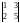 ,
,
 ,
,
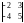 ,
,
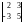
и отметим, что,
например,
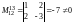 и по определению 4
и по определению 4
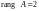 (миноров третьего порядка из элементов
матрицы
составить нельзя, так как
содержит всего две строки).
(миноров третьего порядка из элементов
матрицы
составить нельзя, так как
содержит всего две строки).
Пусть матрица
имеет размер
и
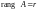 .
Это означает, что хотя бы один минор
порядка
.
Это означает, что хотя бы один минор
порядка
 отличен от нуля, а все миноры порядка
отличен от нуля, а все миноры порядка
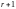 и выше равны нулю. Минор
называется базисным, а столбцы
матрицы, его содержащие, - базисными
столбцами матрицы
(строки, содержащие минор
,
называются базисными строками).
и выше равны нулю. Минор
называется базисным, а столбцы
матрицы, его содержащие, - базисными
столбцами матрицы
(строки, содержащие минор
,
называются базисными строками).
Теорема 1 (о базисном миноре). Столбцы, содержащие базисный минор, линейно независимы. Любой столбец матрицы является линейной комбинацией базисных столбцов одного и того же базисного минора.
Доказательство. Пусть и отличен от нуля минор , расположенный в первых строках и первых столбцах матрицы , т.е. в левом верхнем углу:
 .
.
Докажем сначала, что арифметические векторы
 ,
,
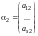 ,
,
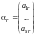
составляют линейно независимую систему.
Допустим, что
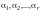 линейно зависимы, тогда
линейно зависимы, тогда
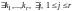 ,
,
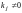 ,
что
,
что
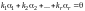 ,
т.е. выполняется система тождеств:
,
т.е. выполняется система тождеств:
 (7.4)
(7.4)
Первые равенств системы (7.4) можно переписать в виде
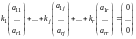 .
.
Учитывая, что , получим
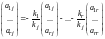 ;
;
-й
столбец определителя
оказался линейной комбинацией остальных.
Тогда
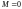 - противоречие, и, следовательно, векторы
линейно независимы.
- противоречие, и, следовательно, векторы
линейно независимы.
Докажем теперь, что любой столбец матрицы является линейной комбинацией первых столбцов.
Рассмотрим вспомогательный определитель
 ,
,
полученный
"окаймлением" минора
элементами
-й
строки и
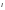 -го
столбца,
-го
столбца,
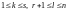 .
Утверждается, что
.
Утверждается, что
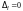 .
.
Действительно, возможны два случая.
Случай 1:
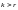 .
Тогда
.
Тогда
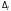 - минор матрицы
порядка
и по условию
(наивысший порядок отличных от нуля
миноров равен
,
следовательно, все миноры порядка
равны нулю).
- минор матрицы
порядка
и по условию
(наивысший порядок отличных от нуля
миноров равен
,
следовательно, все миноры порядка
равны нулю).
Случай 2:
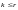 .
Тогда
содержит две одинаковые строки,
следовательно,
.
.
Тогда
содержит две одинаковые строки,
следовательно,
.
Итак, всегда . Разложим по последней строке.
Отметим, что если - алгебраическое дополнение к элементу из последней строки определителя , то
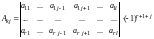 ,
,
и
не зависит от
(
был номером строки в матрице
,
а в
эти элементы занимают
-ю
строку). Поэтому алгебраические дополнения
к элементам
в
,
 ,
можем обозначить
,
можем обозначить
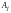 .
.
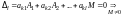
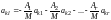 .
.
Полагая
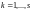 ,
получим
равенств:
,
получим
равенств:
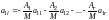 ,
,
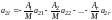 ,
,
…………………………………………
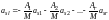 ,
,
или в матричной форме:
 ,
,
т.е.
-й
столбец матрицы
оказался линейной комбинацией первых
столбцов с коэффициентами
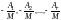 .
.
Было принято, что
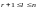 .
.
Если
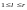 ,
то
,
то
 .
.
Таким образом, любой столбец матрицы является линейной комбинацией базисных столбцов.
Теорема доказана.
Замечание. Аналогичное утверждение справедливо и для строк: строки, содержащие базисный минор, линейно независимы, через них линейно выражаются все остальные строки матрицы.
Теорема 2. Если в матрице некоторый минор порядка отличен от нуля, а все окаймляющие его миноры равны нулю, то .
Доказательство этого утверждения опустим.
Пример 5. Найти ранг матрицы :
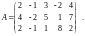
Решение.
Имеем
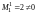 (следовательно,
).
(следовательно,
).
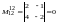 ;
;
 (
( );
);
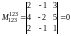 ;
;
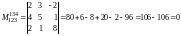 ;
;
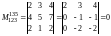 .
.
Таким образом,
известен минор второго порядка, отличный
от нуля (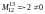 ),
а все миноры третьего порядка, окаймляющие
его, равны нулю, следовательно,
.
),
а все миноры третьего порядка, окаймляющие
его, равны нулю, следовательно,
.
Базисный минор
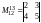 .
Через первый и третий столбцы линейно
выражаются остальные столбцы матрицы.
.
Через первый и третий столбцы линейно
выражаются остальные столбцы матрицы.
Изложенный способ нахождения ранга матрицы называется методом окаймляющих миноров.
