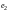Метод элементарных преобразований
Определение 5. Элементарными преобразованиями матрицы называются следующие:
1) перестановка двух строк (столбцов) матрицы;
2) умножение всех
элементов строки (столбца) на вещественное
число
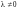 ;
;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Справедливо следующее утверждение, которое приводится без доказательства.
Теорема 3. Элементарные преобразования не изменяют ранга матрицы.
Определение 6.
Матрица
размером
имеет диагональную форму, если
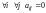 ,
кроме
,
кроме
 ,
,
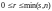 ,
т.е.
,
т.е.
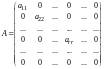 .
.
Отметим, что , так как минор порядка , расположенный в левом верхнем углу (в первых строках и первых столбцах), отличен от нуля, а все миноры, окаймляющие его, равны нулю (они содержат столбец из нулей).
Утверждение. Всякую матрицу элементарными преобразованиями можно привести к диагональной форме.
Действительно, пусть
.
Если , то по определению 6 имеет диагональную форму.
Если
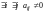 ,
то, переставляя строки и столбцы, можно
добиться того, что
,
то, переставляя строки и столбцы, можно
добиться того, что
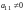 .
Умножим все элементы первой строки на
.
Умножим все элементы первой строки на
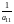 :
:
 .
.
Первую строку,
умноженную на
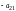 ,
прибавим ко второй, умноженную на
,
прибавим ко второй, умноженную на
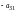 - к третьей,…, умноженную на
- к третьей,…, умноженную на
 - к
-й.
Таким образом, получим матрицу
- к
-й.
Таким образом, получим матрицу
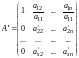 .
.
Первый столбец,
умноженный на
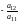 ,
прибавим ко второму,..., умноженный на
,
прибавим ко второму,..., умноженный на
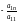 - к
-му,
получим
- к
-му,
получим
 .
.
С матрицей, оставшейся в правом нижнем углу, совершим аналогичные преобразования. После конечного числа шагов придем к матрице диагонального вида.
Пример
6. Найти ранг матрицы
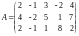 с помощью элементарных преобразований.
с помощью элементарных преобразований.
Решение.
Договоримся об обозначениях. Запись
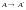 будет означать, что матрица
будет означать, что матрица
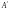 получена из матрицы
с помощью элементарных преобразований.
При этом
-ю
строку исходной матрицы
обозначим
получена из матрицы
с помощью элементарных преобразований.
При этом
-ю
строку исходной матрицы
обозначим
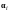 ,
а
-ю
строку преобразованной матрицы
-
,
а
-ю
строку преобразованной матрицы
-
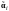 .
Для
-х
столбцов будем использовать соответственно
обозначения
.
Для
-х
столбцов будем использовать соответственно
обозначения
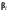 ,
,
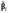 .
.
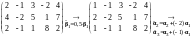
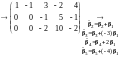
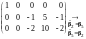
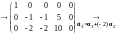
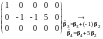
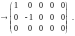
Матрица приобрела
диагональную форму,
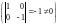 .
.
Упражнение. Найти ранг матрицы методом окаймляющих миноров и методом элементарных преобразований:
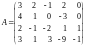 .
.
Лекция 8
Системы линейных алгебраических уравнений
-
Первоначальные понятия. Метод Гаусса
8.1. Метод Гаусса
Пусть дана система
уравнений первой степени (линейных) с
неизвестными. Неизвестные обозначим
 ,
уравнения будем считать пронумерованными:
первое, второе,…,
-е.
Коэффициент из
-го
уравнения при неизвестном
,
уравнения будем считать пронумерованными:
первое, второе,…,
-е.
Коэффициент из
-го
уравнения при неизвестном
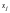 обозначим
,
свободный член -
обозначим
,
свободный член -
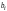 .
.
Система запишется в следующем виде:
 (8.1)
(8.1)
Определение 1.
Решением системы линейных уравнений
(8.1) называется такой набор чисел
 ,
что каждое из уравнений (8.1) обращается
в тождество после замены неизвестных
,
что каждое из уравнений (8.1) обращается
в тождество после замены неизвестных
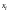 числами
числами
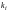 ,
,
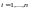 .
.
Определение 2. Система (8.1) называется несовместной, если она не имеет решений, и совместной, если она имеет решения.
Определение 3. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений более одного.
Определение 4. Две системы линейных уравнений называются эквивалентными, если они обе несовместны, или обе совместны и имеют одни и те же решения.
Наиболее удобным для практического разыскания решений системы (8.1) является метод последовательного исключения неизвестных, или метод Гаусса.
Выполним следующие преобразования системы: обе части одного уравнения умножим на некоторое число и прибавим к обеим частям другого уравнения. Покажем, что мы придем к эквивалентной системе.
Пусть обе части первого уравнения системы (8.1), умноженные на число , прибавляются к обеим частям второго уравнения. Получаем систему
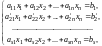 (8.2)
(8.2)
где
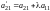 ,
…,
,
…,
 ,
,
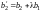 .
.
Пусть - решение системы (8.1). Это означает, что выполняются тождества:
 (8.3)
(8.3)
Равенства (8.3) означают, что набор чисел удовлетворяет первому, третьему,…, -му уравнению системы (8.2). Удовлетворяют эти числа и второму уравнению, так как, если к обеим частям второго тождества в системе (8.3) прибавить обе части первого, умноженные на , получим
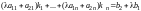 .
.
Таким образом, всякое решение системы (8.1) является решением системы (8.2).
Справедливо обратное. Пусть - решение системы (8.2), тогда
.
 (8.4)
(8.4)
Тождества (8.4)
означают, что набор чисел
удовлетворяет первому, третьему,…,
-му
уравнению системы (8.1). Если к обеим
частям второго тождества в (8.4) прибавить
обе части первого, умноженные на
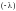 ,
получим
,
получим
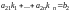 ,
,
то есть удовлетворяют также второму уравнению в (8.1), и всякое решение системы (8.2) является решением системы (8.1). Системы (8.1) и (8.2) в соответствии с определением 4 эквивалентны.
Перейдем к изложению метода Гаусса.
Дана система (8.1).
Пусть
(если это не так, возьмем в качестве
первого любое другое уравнение с
коэффициентом при
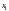 ,
отличным от нуля, и перенумеруем
уравнения; хотя бы одно такое уравнение
найдется, иначе
просто отсутствовал бы).
,
отличным от нуля, и перенумеруем
уравнения; хотя бы одно такое уравнение
найдется, иначе
просто отсутствовал бы).
Обе части первого
уравнения, умноженные на
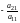 ,
прибавим к обеим частям второго уравнения,
умноженные на
,
прибавим к обеим частям второго уравнения,
умноженные на
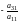 ,
- к обеим частям третьего и т.д., умноженные
на
,
- к обеим частям третьего и т.д., умноженные
на
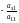 - к обеим частям
-го
уравнения. Придем к новой системе:
- к обеим частям
-го
уравнения. Придем к новой системе:
 (8.5)
(8.5)
Система (8.5) эквивалентна системе (8.1).
Первое неизвестное исключили из всех уравнений системы, начиная со второго.
Уже после первого шага может встретиться уравнение вида
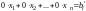 ,
,
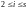 .
(8.6)
.
(8.6)
Если
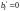 ,
этому уравнению удовлетворяет любой
набор чисел
.
В этом случае уравнение будем отбрасывать.
Если
,
этому уравнению удовлетворяет любой
набор чисел
.
В этом случае уравнение будем отбрасывать.
Если
 ,
уравнению (8.6) не удовлетворяет никакой
набор чисел
,
и система, содержащая такое уравнение
(8.6), несовместна, следовательно,
несовместна и эквивалентная ей система
(8.1). В этом случае преобразования по
методу Гаусса будем прерывать.
,
уравнению (8.6) не удовлетворяет никакой
набор чисел
,
и система, содержащая такое уравнение
(8.6), несовместна, следовательно,
несовместна и эквивалентная ей система
(8.1). В этом случае преобразования по
методу Гаусса будем прерывать.
Итак, имеем систему
(8.5). Среди коэффициентов
,
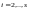 ,
,
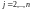 ,
есть отличные от нуля (иначе либо система
несовместна, либо уравнения можно
отбросить). Пусть для определенности
,
есть отличные от нуля (иначе либо система
несовместна, либо уравнения можно
отбросить). Пусть для определенности
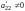 (если
(если
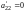 ,
но отличен от нуля коэффициент при
,
но отличен от нуля коэффициент при
 в другом уравнении, можно перенумеровать
уравнения, если
в другом уравнении, можно перенумеровать
уравнения, если
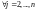
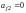 ,
можно перенумеровать неизвестные). Обе
части второго уравнения, умноженные на
,
можно перенумеровать неизвестные). Обе
части второго уравнения, умноженные на
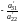 ,
прибавим к обеим частям третьего
уравнения и т.д., обе части второго
уравнения, умноженные на
,
прибавим к обеим частям третьего
уравнения и т.д., обе части второго
уравнения, умноженные на
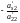 ,
- к обеим частям
-го
уравнения. Этим исключим неизвестное
из всех уравнений, кроме первого и
второго, и придем к системе
,
- к обеим частям
-го
уравнения. Этим исключим неизвестное
из всех уравнений, кроме первого и
второго, и придем к системе

Аналогичным образом продолжим процесс исключения неизвестных.
Если после нескольких шагов получим уравнение вида (8.6), в котором , можно сделать вывод о несовместности системы. Если же такое уравнение не встретится, придем к системе
 (8.7)
(8.7)
эквивалентной
системе (8.1). Здесь
,
,
…,
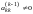 ,
,
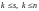 .
.
При
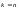 система (8.7) имеет вид
система (8.7) имеет вид
 (8.8)
(8.8)
Из последнего
уравнения найдем значение
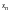 (
(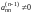 ),
подставим в
),
подставим в
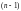 -е,
найдем
-е,
найдем
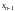 (
(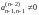 )
и т.д. до первого уравнения, из которого
определится
.
Система (8.8) в этом случае имеет единственное
решение и эквивалентная ей система
(8.1) является определенной.
)
и т.д. до первого уравнения, из которого
определится
.
Система (8.8) в этом случае имеет единственное
решение и эквивалентная ей система
(8.1) является определенной.
При
 в последнем уравнении системы (8.7)
присвоим неизвестным
в последнем уравнении системы (8.7)
присвоим неизвестным
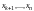 произвольные числовые значения:
произвольные числовые значения:
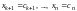 .
.
Из последнего,
-го,
уравнения системы (8.7) найдем
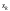 (
),
подставим в
(
),
подставим в
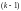 -е
уравнение, найдем
-е
уравнение, найдем
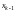 и т.д., двигаясь снизу вверх по системе
(8.7), найдем вполне определенные значения
и т.д., двигаясь снизу вверх по системе
(8.7), найдем вполне определенные значения
 .
Так как значения для неизвестных
можно выбрать бесчисленным множеством
способов, система (8.7) в случае
будет неопределенной.
.
Так как значения для неизвестных
можно выбрать бесчисленным множеством
способов, система (8.7) в случае
будет неопределенной.
Итак, метод Гаусса применим к любой системе линейных уравнений. Если в процессе преобразований встретится уравнение, в котором все коэффициенты при неизвестных равны нулю, а свободный член отличен от нуля, система несовместна. Если такое уравнение не встретится, система совместна. Она является определенной, если приводится к треугольному виду (8.8), и неопределенной, если приводится к трапецеидальному виду (8.7).
Пример. Решить систему методом Гаусса:
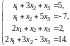
Решение.
Исключаем неизвестное
.
Первое уравнение, умноженное на
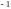 ,
прибавляем ко второму, умноженное на
,
– к третьему и четвертому, получаем
,
прибавляем ко второму, умноженное на
,
– к третьему и четвертому, получаем
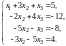
Обе части второго
уравнения умножаем на
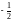 :
:
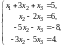 .
.
Второе уравнение, умноженное на , прибавляем к третьему, умноженное на , - к четвертому, получаем:
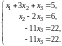
Обе части третьего уравнения, умноженные на , прибавляем к четвертому уравнению, получаем
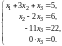
Последнее уравнение
отбрасываем, из третьего уравнения
находим
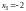 ,
подставляем во второе
,
подставляем во второе
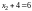 и находим
и находим
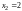 .
Затем
и
.
Затем
и
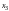 подставляем в первое уравнение
подставляем в первое уравнение
 ,
откуда
,
откуда
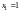 .
.
Итак, , , - решение исходной системы, найденное методом Гаусса.
Лекция 9
Исследование и решение произвольной системы линейных уравнений
Правило Крамера. Исследование произвольной системы линейных алгебраических уравнений. Системы линейных однородных уравнений. Фундаментальная система решений |
9.1. Правило Крамера
Пусть дана система линейных алгебраических уравнений с неизвестными:
 (9.1)
(9.1)
Обозначим
,
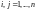 .
.
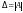 будем называть определителем системы
(9.1).
будем называть определителем системы
(9.1).
Обозначим
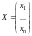 ,
,
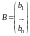 .
Система (9.1) равносильна матричному
уравнению
.
Система (9.1) равносильна матричному
уравнению
. (9.2)
Теорема 1.
Если
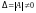 ,
то система (9.1) имеет, притом
единственное, решение.
,
то система (9.1) имеет, притом
единственное, решение.
Доказательство.
Так как
,
то
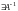 .
Умножим обе части (9.2) на
слева:
.
Умножим обе части (9.2) на
слева:
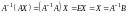 .
.
Итак, решением матричного уравнения (9.2) является матрица - матричное уравнение (9.2) имеет решение, следовательно, система (9.1) совместна.

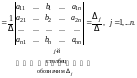 (9.3)
(9.3)
Решение системы
(9.1) дается формулами (9.3), и так как
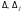 ,
,
вполне определенные числа, единственно.
,
,
вполне определенные числа, единственно.
Теорема доказана.
Правило Крамера:
если
,
то решение системы (9.1) может быть
найдено по формулам
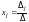 ,
,
где
,
,
где
 - определитель, который получится из
,
если столбец коэффициентов при
заменить столбцом свободных членов.
- определитель, который получится из
,
если столбец коэффициентов при
заменить столбцом свободных членов.
Пример 1. По правилу Крамера, если оно применимо, решить систему
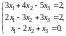
Решение. Имеем
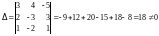 ,
,
следовательно, правило Крамера применимо.
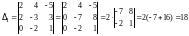 ,
,
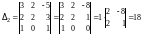 ,
,
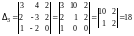 .
.
По формулам (9.3) находим
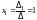 ,
,
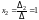 ,
,
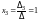 .
.
9.2. Исследование произвольной системы
линейных уравнений
Пусть дана система уравнений с неизвестными:
 (9.4)
(9.4)
Обозначим матрицу
из коэффициентов
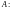
.
Матрица
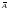 содержит матрицу
и еще столбец свободных членов, она
называется расширенной матрицей
по отношению к
:
содержит матрицу
и еще столбец свободных членов, она
называется расширенной матрицей
по отношению к
:
 .
.
Теорема 2 (Кронекера
- Капелли). Система совместна тогда
и только тогда, когда
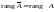 .
.
Доказательство.
Необходимость. Пусть система (9.4)
совместна и
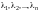 - решение (9.4), следовательно, справедливы
тождества
- решение (9.4), следовательно, справедливы
тождества
 (9.5)
(9.5)
В матрице
к последнему столбцу прибавим первый,
умноженный на
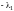 ,
второй, умноженный на
,
второй, умноженный на
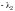 ,…,
-й,
умноженный на
,…,
-й,
умноженный на
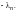 Получим, учитывая (9.5),
Получим, учитывая (9.5),
~ .
.
Поскольку выполнялись
элементарные преобразования, то
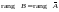 ,
но
,
но
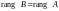 (добавление столбца из нулей не может
изменить ранга), отсюда
(добавление столбца из нулей не может
изменить ранга), отсюда
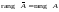 .
.
Достаточность.
Пусть
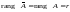 .
Это означает, что существует минор
.
Это означает, что существует минор
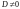 порядка
,
а все миноры порядка
,
окаймляющие
порядка
,
а все миноры порядка
,
окаймляющие
 ,
равны нулю.
,
равны нулю.
Пусть расположен в левом верхнем углу матрицы (это предположение не ограничивает общности рассуждений, так как можно переставить уравнения и перенумеровать неизвестные и тем самым добиться того, что будет расположен в первых строках и первых столбцах матрицы ):
 .
.
Тогда первые
строк матрицы линейно независимы, а
остальные
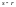 строк являются их линейной комбинацией
(теорема о базисном миноре), следовательно,
через первые
уравнений линейно выражаются остальные
уравнений. Таким образом, вся система
(9.4) эквивалентна первым
уравнениям:
строк являются их линейной комбинацией
(теорема о базисном миноре), следовательно,
через первые
уравнений линейно выражаются остальные
уравнений. Таким образом, вся система
(9.4) эквивалентна первым
уравнениям:
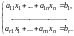 (9.6)
(9.6)
Случай
1:
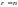 .
Система (9.6) имеет единственное решение
(определитель системы (9.6)
,
- применяем теорему 1). Его можно найти,
например, по правилу Крамера.
.
Система (9.6) имеет единственное решение
(определитель системы (9.6)
,
- применяем теорему 1). Его можно найти,
например, по правилу Крамера.
Случай
2:
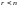 .
Перепишем (9.6) в виде
.
Перепишем (9.6) в виде
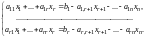 (9.7)
(9.7)
Неизвестные
 назовем главными,
назовем главными,
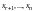 - свободными.
- свободными.
Присвоим свободным
неизвестным произвольные числовые
значения, положим
 .
Тогда согласно теореме 1 из системы
(9.7) определится единственный набор
.
Тогда согласно теореме 1 из системы
(9.7) определится единственный набор
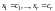 главных неизвестных. Таким образом,
набор
чисел
,
является решением системы (9.4).
главных неизвестных. Таким образом,
набор
чисел
,
является решением системы (9.4).
Значения свободных неизвестных можно выбрать бесчисленным множеством способов, поэтому система (9.4) имеет бесчисленное множество решений.
И в случае 1, и в случае 2 система оказалась совместной. Достаточность доказана.
Определение 1.
Формула, выражающая решение системы
(9.4) в виде вектор-функции
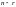 свободных неизвестных, называется
общим решением системы (9.4):
свободных неизвестных, называется
общим решением системы (9.4):
 .
.
Пример 2. Исследовать совместность системы и, если система совместна, найти общее решение и одно частное:
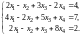
Решение. Найдем ранг матриц и :
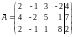 ~
~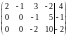 ~
~
~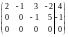 .
.
Итак,
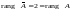 (минор второго порядка
(минор второго порядка
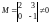 ,
все миноры, его окаймляющие, равны нулю
и в
,
и в
).
Следовательно, согласно теореме 2 система
совместна.
,
все миноры, его окаймляющие, равны нулю
и в
,
и в
).
Следовательно, согласно теореме 2 система
совместна.
Так как
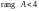 ,
система имеет бесчисленное множество
решений.
,
система имеет бесчисленное множество
решений.
Вся система эквивалентна системе первых двух уравнений:
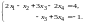
В качестве главных
неизвестных возьмем
и
(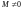 ),
свободных -
и
),
свободных -
и
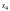 и перепишем систему в виде
и перепишем систему в виде
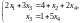 -
-
"укороченная" система.
Отсюда
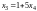 и
и
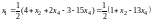 .
.
Общее решение
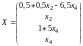 .
.
Частное решение
получим, присвоив конкретные числовые
значения свободным неизвестным, например,
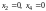 ,
тогда
,
тогда
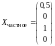 .
.
9.3. Системы линейных однородных
алгебраических уравнений
Пусть дана система линейных однородных уравнений
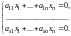 (9.8)
(9.8)
Система (9.8) всегда
совместна (решение
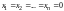 всегда присутствует среди решений).
всегда присутствует среди решений).
Если
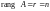 ,
то это решение - единственное, если
,
система (9.8) имеет бесчисленное множество
решений (и, следовательно, есть решения,
отличные от
).
,
то это решение - единственное, если
,
система (9.8) имеет бесчисленное множество
решений (и, следовательно, есть решения,
отличные от
).
Теорема 3. Любая линейная комбинация решений системы однородных линейных уравнений (9.8) является решением системы (9.8).
Доказательство.
Пусть
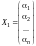 и
и
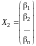 - произвольные решения системы (9.8).
- произвольные решения системы (9.8).
Пусть
- некоторое число,
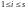 .
Подставим
.
Подставим
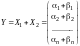
в -е уравнение системы (9.8):
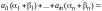
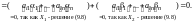
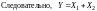 удовлетворяет
-му
уравнению системы (9.8) при произвольном
,
,
т.е.
удовлетворяет
-му
уравнению системы (9.8) при произвольном
,
,
т.е.
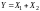 является решением (9.8).
является решением (9.8).
Пусть
- произвольное вещественное число,
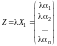 .
.
Подставим
 в
-е
уравнение системы (9.8),
:
в
-е
уравнение системы (9.8),
:

 - решение (9.8).
- решение (9.8).
Итак, сумма любых двух решений системы (9.8) и произведение любого решения на число являются решениями системы (9.8), следовательно, любая линейная комбинация решений системы (9.8) является решением.
Определение 2.
Пусть дана система линейных однородных
уравнений с n
неизвестными
и матрицей
,
.
Пусть неизвестные
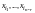 являются свободными.
являются свободными.
Обозначим через
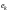 ,
,
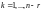 ,
то единственное решение системы, которое
получится, если неизвестному
,
то единственное решение системы, которое
получится, если неизвестному
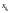 присвоить значение
,
а остальным свободным неизвестным -
значение
.
присвоить значение
,
а остальным свободным неизвестным -
значение
.
Система решений
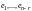 называется фундаментальной системой
решений данной системы линейных
однородных уравнений.
называется фундаментальной системой
решений данной системы линейных
однородных уравнений.
Справедливо следующее утверждение, которое приведем без доказательства.
Теорема 4. Пусть дана система линейных однородных уравнений с матрицей , , и - фундаментальная система решений. Тогда всякое решение системы является линейной комбинацией решений .
Пример 3. Найти общее решение и фундаментальную систему решений системы
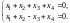 (9.9)
(9.9)
Решение. Первое уравнение, умноженное на , прибавим ко второму:
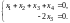
Отсюда
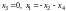 .
.
Общее решение
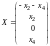 ,
,
свободными являются неизвестные и , главными - и .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы
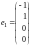 и
и
 составляют фундаментальную систему
решений системы (9.9)
составляют фундаментальную систему
решений системы (9.9)
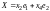 .
.
Последнее равенство можно проверить непосредственно.
Лекция 10
Линейные пространства
-
Аксиоматическое определение линейного
пространства. Базис и размерность
линейного пространства
10.1. Аксиоматическое определение
линейного пространства
Определение 1.
Совокупность
 элементов
элементов
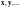 произвольной природы называется линейным
пространством, если для любых элементов
произвольной природы называется линейным
пространством, если для любых элементов
 и
и
 из
установлено понятие суммы
из
установлено понятие суммы
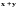 ,
а для любого элемента
из
и любого действительного числа
установлено понятие произведения
элемента
на число
,
обозначаемое
,
а для любого элемента
из
и любого действительного числа
установлено понятие произведения
элемента
на число
,
обозначаемое
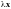 .
При этом для введенных операций выполнены
следующие восемь аксиом:
.
При этом для введенных операций выполнены
следующие восемь аксиом:
1. Сложение коммутативно:
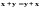 .
.
2. Сложение ассоциативно: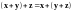 .
.
3. Существует нулевой
вектор
 ,
удовлетворяющий условию
,
удовлетворяющий условию
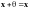 для всех
.
для всех
.
4. Для любого вектора
существует
противоположный вектор
,
удовлетворяющий условию
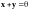 .
.
Для любых векторов
,
и любых действительных чисел
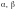 имеют место равенства:
имеют место равенства:
5.
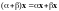 .
.
6.
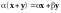 .
.
7.
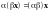 .
.
8.
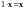 .
.
Элементы линейного пространства принято называть векторами.
Пример
1. Совокупность
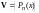 всех многочленов степени
всех многочленов степени
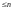 составляет линейное пространство.
составляет линейное пространство.
Решение. Проверим выполнение всех аксиом.
В самом деле, пусть
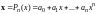 ;
;
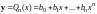 .
.
По правилу сложения двух многочленов имеем
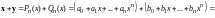
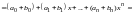
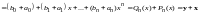 ,
,
следовательно, аксиома 1 выполняется.
Аксиома 2 проверяется аналогично.
В качестве нулевого
вектора берем многочлен, тождественно
равный нулю:
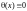 .
.
Для любого многочлена
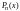 имеет место аксиома 3:
имеет место аксиома 3:
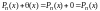 .
.
Проверим выполнение аксиомы 4.
Пусть
- произвольный многочлен из
.
В качестве противоположного элемента
возьмем многочлен
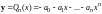 .
По свойству сложения многочленов имеем
.
По свойству сложения многочленов имеем
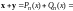
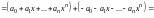
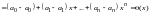 .
.
Таким образом, аксиома 4 верна.
Аксиомы 5 - 8 проверяются аналогично.
Так как все аксиомы линейного пространства выполняются для множества многочленов степени , то является линейным пространством.
Пример 2. Совокупность всех квадратных матриц порядка 2 составляет линейное пространство.
Решение. Проверим выполнение аксиом.
Пусть
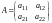 ,
,
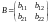 .
.
По правилу сложения матриц
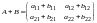 .
.
Но элементы матриц -
вещественные числа, следовательно,
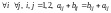 и
и
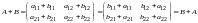 ,
,
аксиома 1 выполняется.
Пусть
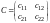 .
.
По правилу сложения матриц
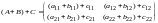 ,
,
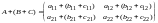 .
.
Так как элементы матриц
- вещественные числа
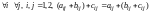 ,
откуда
,
откуда
,
аксиома 2 выполняется.
В качестве нулевого
вектора выступает матрица
 .
.
Действительно, для любой матрицы имеем:
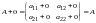 ,
,
аксиома 3 выполняется.
Для произвольной матрицы
в качестве противоположного элемента
возьмем матрицу
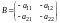 .
.