Примеры моделирования клеточных автоматов

В статье [8] рассматривается моделирование с использованием клеточных автоматов, для решения вопросов связанных с Эффективными Базовыми Операциями (Effects-Based Operations).

По мнению автора клеточные автоматы являются дискретными динамическими системами и их эволюция полностью определяется состоянием его атомных элементов и их локальными взаимодействиями. Поэтому их можно рассматривать, как дискретные идеализированные уравнения в частных производных. Отличительной чертой для этого подхода является в расположении моделей атомных элементов и установка правил их взаимодействия. Эта простота на атомном уровне, тем не менее организует сложное глобальное поведения развития при взаимодействии многочисленных элементов.

Существуют некоторые классические и базовые установленные правила клеточных автоматов [Wolfram (1994), Hegselmann and Flache (1998), Casti (1992), Toffoli & Margolus (1987)]:

- автомат состоит из постоянной N-мерной решётки ячеек.

- каждая ячейка или клетка в автомате, может находится в одном из конечных определённых состояний.

- автомат развивается с течением определённого количества временных этапов.

- состояние всех клеток в автомате обновляется одновременно на каждом шаге.

- клетки изменяют своё состояние в соответствии с локальными правилами, другими словами состояния перехода каждой ячейки определяется из состояния самой ячейки и её соседей.

Рисунок 1.3 - Правило четырёх соседей фон Неймана, здесь клетка С имеет четыре соседа (E, N, W и S), состояние которых и будет определять её дальнейшую судьбу.

Рисунок 1.4 - Правило восьми соседей Мура, в данном случае клетка С имеет уже восемь соседей (N, NE, E, SE, S, SW, W, NW).

Рисунок 1.5 - Двумерный клеточный автомат, в котором клетки ограничены в квадратной сетке размером 25х25, различное состояние каждой клетки определяется её цветом, который закодирован определённым тоном и оттенком.

В данной двумерной плоской структуре решетки, имеется одна проблема, связана она с тем, что на левом крае решётки, клетки не имеют западных соседей, из-за этого на восточной стороне так же уменьшается количество соседей у граничных клеток. Подобное положение ячеек у северной и южной стороны.

Исправляется этот недочёт "приклеиванием" левого края решётки к правому, а верхний край приклеиваются к нижней части. Это преобразует плоскую структуру, к структуре решётки формы тора. В таком виде у каждой ячейки имеется полноценное количество соседей.

Рисунок 1.6 - Двумерный клеточный автомат, в котором левая часть "приклеена" к правой, а верхняя к нижней.

Если представить, что определяет правило перехода для каждой ячейки, а C(t) представляет собой состояние ячейки C на шаге времени t, с аналогичными обозначениями для других клеток, то состояние ячейки С при следующем шаге t+1, для правил окрестности фон Неймана, будет определяться выражением:

.

Это правило применяется одновременно и несколько раз для каждой ячейки в автомате, на каждом этапе эволюции. Это правило может быть очень простым или сложным.

Интересным фактом является то, что клеточный автомат управляемый довольно простыми локальными правилами в результате довольно часто демонстрирует очень сложное глобальное поведение.

Так же в [8] статье рассматривается моделирование клеточных автоматов, как оппонента систем Pol-Mil-Sec.

Самовоспроизведения в тривиальном смысле — без использования конфигураций, включающих в себя машину Тьюринга, — добиться легко. Удивительно простой пример «тривиальной» самовоспроизводящейся системы предложил около 10 лет назад Эдвард Фредкин. В этой системе ячейки могут находиться лишь в двух состояниях, каждая из них, как и в примере фон Неймана, имеет четырёх соседей, а правила перехода сводятся к следующим. Каждая клетка, имеющая в момент времени t четное число (0, 2, 4, ...) живых соседей, в момент времени t + 1 становится пустой (то есть переходит в нулевое состояние или, если она уже находилась в нулевом состоянии, остаётся в нём). Каждая клетка, имеющая в момент времени t нечетное число (1, 3, ...) соседей, в момент времени t + 1 становится живой (то есть переходит в ненулевое состояние или сохраняет его, если она уже в нём находилась). Через 2ⁿ ходов (число n зависит от выбора конфигурации) любая конфигурация живых клеток в таком пространстве воспроизведет себя четыре раза: одна копия расположится справа, другая — слева, третья — сверху, четвёртая — снизу от того (уже пустого) места, где находилась начальная конфигурация. Новая конфигурация через 2ⁿ шагов снова размножится (с коэффициентом воспроизводства, равным 4) и т. д. Число копий увеличивается в  геометрической прогрессии 1, 4, 16, 64... На рисунке 1.1 показаны полтора цикла размножения тримино в форме прямого угла.

Рисунок 1.1 - эволюция тримино в форме прямого угла в шести шагах.

Терри Виноград в 1967 году обобщил правила Фредкина на любое число соседей, произвольную схему примыкания клеток и размерность (результаты Винограда относятся к клеткам, число состояний которых просто).

Существует множество автоматов такого рода, отличающихся друг от друга схемой примыкания соседних клеток. числом состояний и правилами перехода, в 1967 С. Улам исследовал и описал несколько подобных примеров КА. На рисунке показано сорок пятое поколение организма, родившегося из одной-единственной фишки, стоявшей в центральной клетке.

Рисунок 1.2 - Сорок пятое поколение клеточного автомата С. Улама, произошедшего из единственной фишки в центре.

Как и в игре Конуэя, клетки в игре Улама могут находиться в двух состояниях, но соседними считаются клетки, примыкающие к данной лишь по вертикали, но не по диагонали («соседи» в смысле фон Неймана). Рождение фишки происходит на клетке, имеющей одного и только одного соседа, а все клетки поколения nпогибают после рождения поколения n + 2. Иначе говоря, на любом этапе эволюции выживают лишь два последних поколения. На рисунке черными изображены новорожденные клетки (их 444). Зеленые клетки предыдущего поколения — их 404 — исчезнут на следующем ходу. Обратите внимание на характерную деталь, которую Улам назвал «обглоданной костью». Улам проводил эксперименты и с такими играми, в которых две конфигурация могли расти до тех пор, пока они не сталкивались. В следующей за столкновением «битве» одной стороне иногда удавалось одержать верх над другой, а иногда обе армии исчезали. Улам рассмотрел также игры на трёхмерных досках — кубических «паркетах», заполняющих всё пространство. Основные результаты Улама собраны в его статьях, опубликованных в сборнике «Очерки теории клеточных автоматов» (Essays on Cellular Automata, University of Illinois Press, 1970, ed. by Arthur W. Burks).

Аналогичные игры можно вести и на бесконечных досках, клетки которых имеют форму равносторонних треугольников и правильных шестиугольников. Несмотря на сильное внешнее отличие, по существу эти игры не вносят ничего нового, и с помощью подходящего определения «соседних» клеток их всегда можно свести к эквивалентным играм на обычной доске с клетками в форме квадратов. Соседними могут быть не только клетки, имеющие общие стороны или вершины. Например, в шахматах для клетки, на которой стоит конь, соседними (то есть влияющими на её состояние) считаются все клетки, на которые можно пойти конём или на которых стоят угрожающие ему фигуры. Как заметил Беркс, такие игры, как шахматы, шашки и го, допустимо рассматривать как клеточные автоматы со сложными окрестностями каждой клетки (окрестностью называется совокупность соседей) и правилами перехода. Противники, делая очередной ход, выбирают среди множества допустимых состояний то, которое должно привести их к определённому конечному состоянию  - выигрышу.

В публикации [9] рассмотрена игра клеточных автоматов «FireSquad» с точки зрения применения в качестве формальной модели синхронизации действий в распределённых программных системах. Описаны эвристики, позволяющие сократить пространство вариантов при поиске минимального локального правила.

Рассматриваются основные приемы оптимизации переборной стратегии для игры «Firing squad». Интерес представляет минимизация числа возможных состояний элементов, числа возможных ситуаций для элемента (состояние самого элемента и его соседей) и количества временных интервалов до залпа.

К примеру была поставлены задача найти локальное правило, удовлетворяющее «Fired squad» для заданного числа элементов n и числа используемых состояний

k. Пусть генерал стоит первым в строю. Локальное правило описывается функцией F(x, y, z), которая возвращает значение нового состояния элемента (0,1,..., k–1) в зависимости от текущих состояний элемента (x = 0,1,..., k–1) и состояний его соседей (y = 0,1,..., k–1 и z = 0,1,..., k–1). Известно, что F(0, 0, 0) = 0. Значение функции в других точках необходимо подобрать. В начальном состоянии необходимо определить лишь два значения функции для перехода в следующее состояние:

F(1, 0, 0) = a, F(0, 1, 0) = b.

Для следующего шага – (см. рис. 3):

рF(a, 0, b) = c, F(b, a, 0) = d, F(b, a, 0) = e.

Рисунок 1.7 - Изменение конфигурации клеточного автомата с течением времени.

И так далее. Для определения всего множества конфигураций клеточного автомата до залпа необходимо определить лишь требуемую часть значений функции. На каждом шаге необходимо определить лишь 1–4 значений (с течением времени это число уменьшается). Определив, что число шагов до залпа не должно превышать 3n, получаем снижение числа перебираемых локальных правил порядка k⁸ⁿ.

В современных распределённых программных системах требуется использование формальных подходов к выработке единого коллективного решения среди большого количества независимых программных сущностей, в данной работе эти подходы так же рассматриваются.

В своих статьях А. Колесников [10] ведёт рассказ о классической игре Дж. Конвэя - "Жизнь", её классических правилах. Рассматриваются возможности её преобразования и модернизация к более реалистичному виду. Проводится моделирование клеточных автоматов с большим числом возможных состояний. В процессе эволюции на клеточном поле формируются изменчивые замысловатые кольцевые структуры, в которых чередуются зоны с высокой и низкой заселенностью. Эти картины сильно напоминают некие микробные колонии. Виртуальные микробы копошатся, растекаются, делятся, одним словом - живут. Возможно, описанную игру следовало бы назвать "Хаос", поскольку то, что происходит на экране, пожалуй, точнее всего можно определить именно как хаос. Причем речь идет не о скучном статистическом хаосе пустого рябящего телевизионного экрана, а о хаосе в космогоническом античном смысле - о хаосе первородного кипения формотворящих сил, которые в конечном счете и породили то, что называется "Жизнь". В своей статье "Клеточные автоматы и компьютерная экология", автор рассматривает моделирование распространения загрязнения в экологической среде. Сам характер этого процесса указывает на то, что для моделирования рассеивания загрязнителя в атмосфере можно использовать подход, основанный на идеологии клеточных автоматов. В этом случае исследуемый участок представляется в виде клеточного поля. На поле помечаются клетки, в которых находятся эпицентры распространения загрязнения или заражения. Затем концентрацию загрязнителя в каждой клетке поля можно, например, приближенно оценивать по формуле:

₍₁₎

где - это массив из девяти элементов, содержащий вероятности ветров соответствующих восьми направлений и вероятность штиля. Само собой разумеется, что девять вероятностей ветров различных направлений, включая вероятность штиля, должны в сумме давать единицу.  - это вектор из девяти элементов, содержащий концентрации загрязнителя в соседних с данной восьми клетках и в ней самой.

Шаг за шагом для всех клеток поля вычисляется сумма произведений концентраций в соседних восьми ячейках на соответствующие вероятности ветров. К сумме прибавляется еще и произведение вероятности штиля на концентрацию загрязнителя в самой текущей клеточке. Для нормальной работы программы необходимо иметь две копии клеточного поля. В одной из копий следует хранить предыдущее поколение, а в другой - последующее.

При смене поколений содержимое последующего поколения становится предыдущим. Из расчетов исключаются крайние ряды ячеек. Это делается для того, чтобы избежать "пограничных" проблем при применении формулы (1). Повторяя расчеты многократно, мы можем наблюдать динамику формирования эллипсоидов рассеивания во времени. При разовом "впрыске" загрязнителя в какую-либо ячейку он быстро рассасывается по клеточному массиву. Для получения более выразительной картины рассеивания в предлагаемом на врезке фрагменте программного кода "впрыск" загрязнителя в соответствующие ячейки осуществляется в начале расчета каждого очередного поколения. Значения концентраций выбросов вводятся в ячейки в неких произвольных единицах.

Р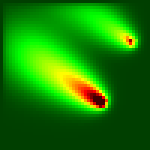 исунок 1.8 - Пример рассеивания загрязнения в среде. Моделирование проводиться с применением клеточных автоматов.

Для восприятия результатов моделирования важна раскраска клеток. В приведенном программном фрагменте использован алгоритм, переводящий значения концентраций загрязнителя в различные градации яркости цветов - от темно-красного до темно-зеленого. При этом высокие значения концентраций изображаются оттенками красного, который, по мере снижения Z, переходит в желтый, а затем постепенно затухает до темно-зеленого цвета. Конечно, для по-настоящему точных моделей процессов рассеивания атмосферных загрязнителей следует обращаться к намного более прецизионным методикам, чем та, о которой шла речь.

При помощи этой несложной программки вы можете выполнить некое небольшое занимательное мини-исследование по компьютерному моделированию экологической ситуации в вашем районе, городе или области в пределах определённых временных рамок.

DefByte I-K

DefInt L-N

Dim G As Byte

Dim a(1 To 9) As Single

Dim b(1 To 200, 1 To 200) As Single

Dim c(1 To 200, 1 To 200) As Single

Dim Color As Long

Dim Zmin As Single

Dim Zmax As Single

Dim R As Single

Dim R4 As Single

Dim Z14 As Single

Dim Z24 As Single

Dim Z34 As Single

Private Sub Form_Click()

a(1) = 0.05

a(2) = 0.05

a(3) = 0.1

a(4) = 0.1

a(5) = 0.1

a(6) = 0.1

a(7) = 0.1

a(8) = 0.15

a(9) = 0.25

z = 7

Zmin = 0

Zmax = 2

R = Zmax - Zmin

R4 = R / 4

Z14 = Zmin + R4

Z24 = Z14 + R4

Z34 = Z24 + R4

n = 50

G = 50

For f = 1 To G

b(35, 35) = z

b(45, 15) = z / 2

For i = 2 To n - 1

For j = 2 To n - 1

c(i, j) = 0

k = 0

For l = -1 To 1

For m = -1 To 1

k = k + 1

c(i, j) = c(i, j) + a(k) * b(i + l, j + m)

Next m

Next l

Next j

Next i

For i = 1 To n

For j = 1 To n

Color = SetColor(c(i, j))

Line (6 * (i - 1), 6 * (j - 1))-(6 * i - 1, 6 * j - 1), Color, BF

b(i, j) = c(i, j)

Next j

Next i

Next f

End Sub

Public Function SetColor(z As Single) As Long

Dim t As Byte

Select Case z

Case Is < Zmin

SetColor = RGB(0, 63, 0)

Case Zmin To Z14

t = 63 + 192 * (z - Zmin) / R4

SetColor = RGB(0, t, 0)

Case Z14 To Z24

t = 255 * (z - Z14) / R4

SetColor = RGB(t, 255, 0)

Case Z24 To Z34

t = 255 * (1 - (z - Z24) / R4)

SetColor = RGB(255, t, 0)

Case Z34 To Zmax

t = 63 + 192 * (1 - (z - Z34) / R4)

SetColor = RGB(t, 0, 0)

Case Is > Zmax

SetColor = RGB(63, 0, 0)

End Select

End Function

Так же затрагивается тематика возможности создания гомункулуса и других себе подобных живых существ. Определённые успехи в области моделирования необыкновенных "жизнеподобных" химических реакций в современной науке все же достигнуты. Огромный шаг в этом направлении совершил сразу после войны советский ученый Белоусов.

В процессе реакции, открытой Белоусовым, из первичного хаоса смеси реагентов рождаются макроскопические упорядоченные структуры в форме кольцевых волн. Это, конечно, пока еще не гомункулус, но существенный шаг вперед по пути моделирования химических процессов нового типа - самоорганизационных процессов. А именно они и лежат в основе возникновения и эволюции живых систем.

Автор рассматривает одну из игр, принадлежащих к играм клеточных автоматов, в котором удивительным образом соединились химия, компьютерные науки и современная теория самоорганизации. Речь идёт о так называемой перемешивающей машине. Перемешивающая машина - это своеобразное развитие знаменитой клеточной модели жизни Дж. Конвэя. Как и все клеточные автоматы, перемешивающая машина представляет собой матрицу, состоящую из множества параллельно взаимодействующих друг с другом ячеек. Именно таким образом организованные параллельные вычислительные устройства, по мнению многих теоретиков искусственного интеллекта, позволят приблизиться к решению проблемы моделирования настоящих мыслительных процессов. Правила взаимодействия ячеек в перемешивающей машине таковы, что дают возможность моделировать волновые структуры, точь в точь напоминающие те, которые можно наблюдать в уже упоминавшейся химической реакции, открытой Белоусовым.

Клеточный автомат "Перемешивающая машина" был предложен М. Герхардом и Х. Шустером. Правила взаимодействия ячеек автомата Герхарда и Шустера удобно излагать, используя эпидемическую терминологию. Отдельная клетка может находиться в некотором множестве состояний. Обозначим их целыми числами от 0 до n. Клетки, находящиеся в состоянии 0, будем называть здоровыми, а клетки, находящиеся в состоянии n, - больными. Все остальные промежуточные состояния интерпретируются как зараженность различной степени. Иными словами, клетка в рассматриваемой модели может быть либо здорова, либо заражена, либо больна. В зависимости от того, к какому из этих трех типов клетка относится в данный момент времени t, ее судьба в момент времени t+1 складывается по-разному. Если клетка здорова (то есть ее состояние x(i,j)=0), то ее состояние в момент времени t+1 будет определяться формулой:

,

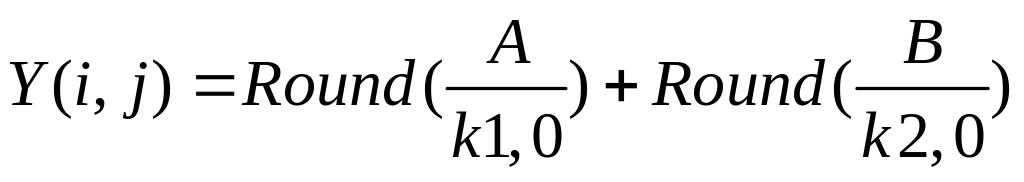Здесь A - это количество зараженных, а B - количество больных клеток в окрестности. Константы k1 и k2 представляют собой некие изначально задаваемые управляющие параметры. Функция Round возвращает округленное до указанного количества знаков значение выражения.

Если в момент времени t клетка заражена (то есть x(i,j) имеет любое значение, большее 0, но меньшее n), то в момент времени t+1 ее состояние будет определяться формулой:

,

Здесь, как и прежде, А - количество зараженных соседей в окрестности клетки, а S - это сумма состояний всех соседних клеток, включая саму X(i,j). Константа G также представляет собой некий изначально задаваемый управляющий параметр. Следует помнить, что Y(i,j) ни при каких условиях не может превышать максимального значения n. Поэтому, если в процессе вычислений значение выходит за эти рамки, его следует приравнять к n.

Наконец, если клетка в момент времени t больна (то есть, ее состояние равно n), то в следующий момент времени t+1 она всегда переходит в состояние 0, то есть выздоравливает.

Программный код, моделирующий поведение перемешивающей машины:

Dim x(210, 210) As Integer

Dim y(210, 210) As Integer

Dim c As Byte

Dim n As Byte

Dim m As Byte

Dim k1 As Single

Dim k2 As Single

Dim g As Byte

Private Sub Form_Click()

For f = 1 To 150

x(0, 0) = x(n, n): x(0, n + 1) = x(n, 1): x(n + 1, 0) = x(1, n): x(n + 1, n + 1) = x(1, 1)

For k = 1 To n

x(0, k) = x(n, k): x(k, 0) = x(k, n): x(n + 1, k) = x(1, k): x(k, n + 1) = x(k, 1)

Next k

For i = 1 To n

For j = 1 To n

Select Case x(i, j)

Case Is = 0

a = 0: b = 0

For k = i - 1 To i + 1

For l = j - 1 To j + 1

Select Case x(k, l)

Case 1 To m - 1

a = a + 1

Case Is = m

b = b + 1

End Select

Next l

Next k

y(i, j) = Round((a / k1), 0) + Round((b / k2), 0)

blue = 0: red = 0: green = 0

Case 1 To m - 1

a = 0: s = 0

For k = i - 1 To i + 1

For l = j - 1 To j + 1

If x(k, l) > 0 And x(k, l) < m Then a = a + 1

s = s + x(k, l)

Next l

Next k

y(i, j) = Round((s / a), 0) + g

If y(i, j) > m Then y(i, j) = m

Case Is = m

y(i, j) = 0

End Select

c = (x(i, j) / m) * 255

Line (4 * (i - 1), 4 * (j - 1))-(4 * i - 1, 4 * j - 1), RGB(c, c, c), BF

Next j

Next i

For i = 1 To n

For j = 1 To n

x(i, j) = y(i, j)

Next j

Next i

Next f

End Sub

Private Sub Form_Load()

Randomize

n = 25

m = 100

k1 = 5

k2 = 4

g = 28

For i = 1 To n

For j = 1 To n

x(i, j) = m * Rnd

Next j

Next i

End Sub

 

Для того, чтобы не изменять общие правила на границах поля, клеточная матрица "сворачивается" в тор. Процедура сворачивания лишает поверхность ее границ, а значит, и "пограничных" проблем. Для хранения состояний ячеек в предыдущем и последующем поколении используются два двухмерных массива - X(i,j) и Y(i,j). Результат выводится на форму в виде мозаики квадратиков, раскрашенных в градации серого цвета в соответствии с состояниями ячеек в момент времени t. При моделировании перемешивающей машины рекомендуется использовать анимационные технологии, поскольку динамика образования и движения волновых фронтов производит совершенно неповторимое впечатление именно в движении.

Как и во многих других играх клеточных автоматов, в поведении перемешивающей машины угадываются биоподобные черты. Клеточная плазма, первоначально хаотическая, начинает беспокойно пульсировать. Постепенно ее пульсации становятся все более регулярными и, наконец, в ее недрах рождаются устойчивые центры, генерирующие медленно распространяющиеся во все стороны ряды кольцевых волн.

В описанной игре воспроизводится удивительное явление самоорганизации, которому, по существу, обязан своим существованием и окружающий нас мир, и мы сами. Из хаотической смеси находящихся в случайных состояниях клеточек постепенно сами собой возникают некие макроскопические образования. Массивы клеток согласованно циклически меняют свои состояния, кооперируясь в связные коллективные структуры.

В данной книге [11] авторы описывают методы моделирования в сочетании с использованием клеточных автоматов. По их мнению данный метод довольно эффективен и может использоваться в сбалансированной и не сбалансированной статистической физике, ориентированных приложениях и комплексных системах. Основные идеи и концепция представлены на конкретных примерах, для конкретного описания данного метода. Основные обсуждаемые разделы данной книги - применение клеточных автоматов в физике, в динамических и распространяющихся системах, моделирования распространения КА с различными правилами роста клеток. Так же рассматриваются диффузионные системы, модели структур газовых автоматов и клеточные автоматы вида полоски или кольца.