I Элементы линейной алгебры

Линейная алгебра – раздел алгебры, изучающий линейные преобразования в конечномерных линейных пространствах.

1. Матрицей называется прямоугольная таблица, составленная из элементов различной природы, содержащая m строк и n столбцов.

Если m ≠ n, матрица называется прямоугольной, размерности m _x n. Если m = n, матрица наз квадратной порядка m или n.

Диагональ, проведённая из левого верхнего угла в правый нижний, называется главной диагональю матрицы, а из левого нижнего в правый верхний – побочной диагональю.

Квадратная матрица, у которой все элементы, стоящие на главной диагонали равны 1, а все остальные равны нулю, называется единичной и обозначается буквой Е.

Две матрицы одинаковой размерности называются равными, если у них равны все соответствующие элементы.

Матрица, у которой все элементы а_ij=0, называется нулевой.

Если в прямоугольной матрице поменять местами все строки и столбцы, то матрица называется транспонированной (А^Т).

Сложение и вычитание: можно только матрицы одинаковой размерности. При сложении нужно сложить соответствующие элементы, а при вычитании – вычесть.

Умножение матрицы на число: нужно все элементы матрицы умножить на это число.

Законы: Коммутативный (переместительный): А+В=В+А, А∙λ=λ∙А. Ассоциативный (сочетательный): (А+В)+С=А+(В+С). При сложении с нуль-матрицей матрица А не меняется: А+0=А.

Для любой матрицы А существует противоположная –А, такая, что А+(-А)=0. Дистрибутивный (распределительный): (А+В)∙λ=А∙λ+В∙λ.

Умножение матриц: Умножить матрицу А на В можно только в том случае, если число столбцов матрицы А равно числу строк матрицы В. Число строк новой матрицы такое же, как у первой А, а число столбцов такое же, как у второй В.

2. Определителем или детерминантом квадратной матрицы А называется число, полученное из её элементов по определённому закону: ∆ или det А=матрица=а₁₁∙а₂₂-а₂₁∙а₁₂.

Определителем квадратной матрицы третьего порядка называется число, полученное из её элементов по следующему правилу: треугольника.

Минором М_ij для элемента a_ij определителя называется новый определитель, который получается из данного путём вычёркивания той строки и столбца, на пересечении которых стоит данный элемент.

Алгебраическим дополнением элемента а_ij определителя называется минор M_ij этого элемента, взятый со знаком (-1)^i+j (т.е. с плюсом, если i+j чётное число, с минусом, если i+j нечётное).

Свойства определителя. 1) при транспонировании матрицы её определитель не меняется. 2) при перестановке двух строк (столбцов) определителя он меняет свой знак на противоположный. 3) Если в определителе имеется две одинаковые строки (столбца), он равен нулю. 4) при умножении элементов какой-то строки (столбца) на число, он умножается на это число, т.е. множитель можно вынести за определитель. 5) если в определителе элементы двух строк (столбцов) пропорциональны, то он равен нулю. 6) Если в определителе есть нулевая строка (столбец), то он равен нулю. 7) Если каждый элемент какого-то столбца (строки) определителя представляет собой сумму двух слагаемых, то определитель можно представить в виде суммы определителей. 8) Величина определителя не изменится, если к элементам какой-то строки (столбца) прибавить элементы другой строки (столбца), умноженные на общий множитель. 9) (разложение определителя по строке или столбцу) Любой определитель равен сумме произведений элементов какой-то строки (столбца) на соответствующие алгебраические дополнения. 10) Сумма произведений элементов какой-то строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю.

3. Система n линейных уравнений с n неизвестными имеет вид:

,

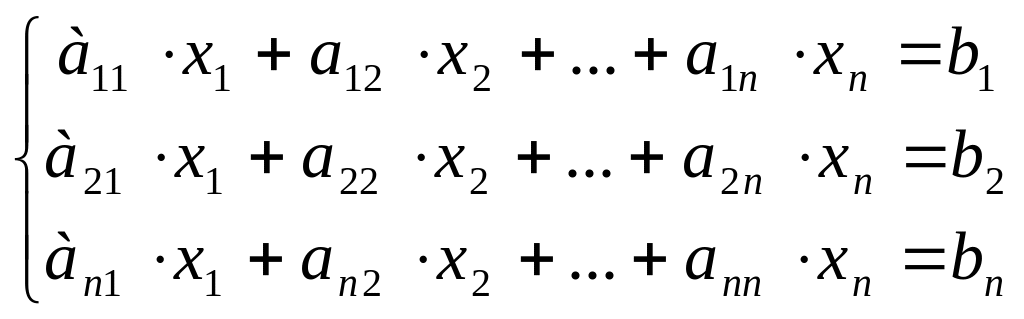Главный определитель системы:

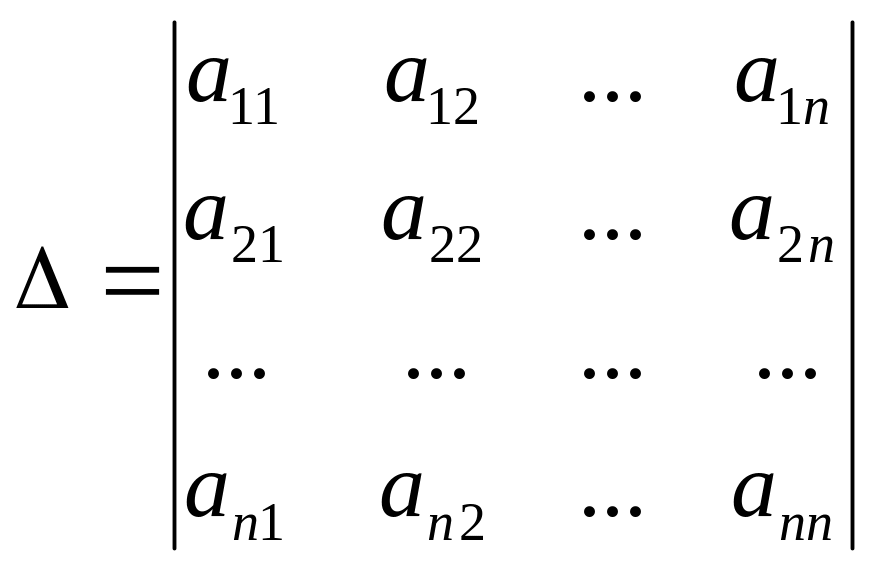
Если определитель ∆≠0, то система всегда совместна и имеет единственное решение, которое определяется по формулам: х₁=∆х₁/∆; х_n=∆x_n/∆ (формулы Крамера).

;

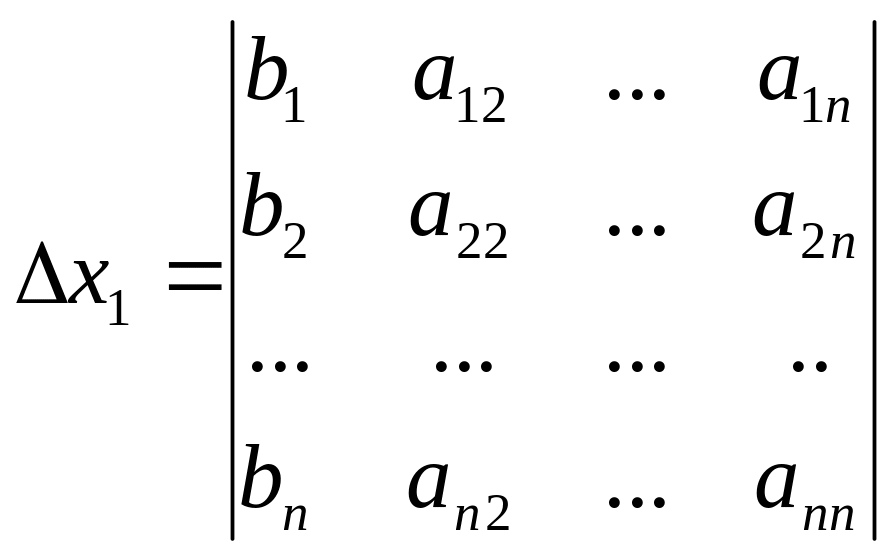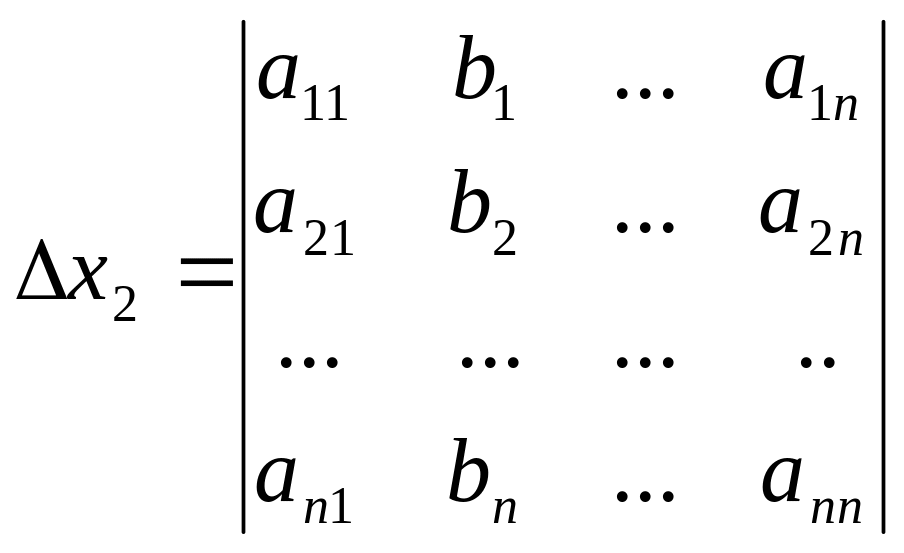
Если ∆=0, а хотя бы один ∆х_i≠0, то система несовместна, т.е. не имеет решения.

Если ∆=0 и ∆х_i=0, то система не определена (т.е. много решений), либо несовместна, поэтому нужны дополнительные исследования. Исследовать систему значит решить вопрос о количестве её решений, либо убедиться в их отсутствии.

4. Рангом матрицы А называется максимальный порядок отличного от нуля минора матрицы. Обозначается r(А). Если ранг матрицы равен r(А)=к, то это значит, что найдётся в матрице хотя бы один минор к-го порядка, отличный от нуля, а все миноры к+1,к+2 и т.д. равны 0. Если матрица не нулевая, то её ранг всегда r(а)≥1.

Свойства ранга. Ранг не меняется: 1) при перестановке любых строк (столбцов) матрицы. 2) при умножении (делении) элементов какой-то строки (столбца) на произвольный множитель. 3) если удалить из матрицы чисто нулевую строку (столбец). 4) если удалить из матрицы все одинаковые строки (столбцы), кроме одной(го). 5) Если к элементам любой строки (столбца) прибавить элементы другой строки (столбца), умнож на произвольное число, λ.

Исследование системы. Пусть имеется система линейных уравнений. Исследовать любую систему значит решить вопрос о количестве её решений, либо убедиться в их отсутствии. Если к матрице системы (А) присоединить столбец свободных членов, то получится расширенная матрица (Ā).

Теорема Кронекера-Капелли. Для совместимости системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы этой системы.

Т.е. если r(А)=r(Ā) – система совместна, если r(A)≠r(Ā) – система несовместна. Если в случае совместности системы нужно выяснить вопрос о количестве решений, то нужно ранг сравнить с числом неизвестных: а) если r(А)=r(Ā)=n, то система имеет единственное решение (n – число неизвестных в системе). б) если r(А)=r(Ā)=к<n, то система имеет множество решений.

5. Метод Гаусса иначе называется методом последовательного исключения неизвестных, суть которого состоит в том, что на 1 этапе неизвестное Х₁ исключается из всех уравнений системы, кроме первого. На 2 этапе неизвестное Х₂ исключается из всех уравнений, кроме 1-го и 2-го. На третьем этапе исключается неизвестное Х₃ из всех уравнений кроме 1-го, 2-го и 3-го, и т.д. В результате этих преобразований система линейных уравнений приводится к специальному треугольному или трапецеидальному виду. Если число уравнений меньше числа неизвестных, то система приводится к трапециидальному виду, если число уравнений равно числу неизвестных, то к треугольному. В системе: 1) можно каждую строку матрицы умножать или делить на одно и то же число. 2) можно строки и столбцы переставлять. При перестановке столбцов указывать новый порядок неизвестных. 3) можно удалять чисто нулевые строки. 4) из всех одинаковых строк удалять все, кроме одной. 5) к элементам любой строки прибавлять и вычитать элементы другой строки, умноженные на общий множитель. Исследование: Если после преобразований в матрице получилась противоречивая строка 000...0|b, то система несовместна, т.е. нет решений. Если нет противоречивой строки, то система совместна, если она приведена треугольному виду, то решение единственное, если нет, то бесчисленное.

6. Квадратная матрица называется невырожденной, если её определитель не равен нулю.

Матрица В называется обратной для матрицы А, если их произведение равно единичной матрице. Матрица, у которой существует обратная, называется обратимой. Теорема (необходимое и достаточное условие существования обратной матрицы): Для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля. Следствия: а) матрица должна быть квадратной; б) определитель её не равен нулю, т.е. невырожденность матрицы гарантирует существование обратной матрицы.

Вычисление обратной матрицы. Дана квадратная матрица. Для вычисления обратной матрицы A^-1 нужно: 1) вычислить определитель матрицы. Если он отличен от нуля продолжить вычисления, если равен нулю, то обратная не существует. 2) Найти для матрицы А присоединённую А^*. присоединённая матрица – это транспонированная матрица алгебраических дополнений для элементов матрицы А. 3) разделить полученную матрицу А^* на определитель detA.

Решение матричных уравнений: A∙X=B,

A^-1∙A^-1∙X=A^-1∙B→E∙X=A^-1∙B

Решение линейных уравнений. Дана система n линейных уравнений с n неизвестными.

а₁₁х₁+а₁₂х₂+...+а_1nx_n=b₁

а₂₁х₁+а₂₂х₂+...+а_2nx_n=b₂

Если ввести матрицы следующим образом:

,

Такая система может быть записана виде одного матричного уравнения: А∙Х=В. Формула для его нахождения Х=А^-1∙В. Если матрицы А, В, Х протранспонировать, тогда систему можно записать в виде матричного уравнения Х∙А=В. Формула для решения Х=В∙А^-1.