Математический анализ

Глава 1

1. Функции нескольких переменных

   1. Основные понятия

Пусть задано множество упорядоченных пар . Соответствие , которое каждой паре чисел ставит в соответствие одно и только одно число , называется функцией двух переменных, определенной на множестве со значениями в , и записывается в виде или . При этом и называются независимыми переменными (аргументами), а – зависимой переменной (функцией).

Множество называется областью определения функции. Множество значений, принимаемых в области определения, называется областью изменения этой функции, обозначается или .

Функцию , где можно понимать (рассматривать) как функцию точки координатной плоскости . В частности областью определения может быть вся плоскость или её часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, и обозначается . Примером замкнутой области является круг с окружностью.

Значение функции в точке обозначают или и называют частным значением функции.

Геометрический смысл: Каждой точке области в системе координат соответствует точка , где – аппликата точки . Совокупность таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию .

Пример

Функция , имеет областью определения круг и изображается сферой с центром в точке и радиусом .

Функция двух и более числа переменных может быть задана, как и функция одной переменной разными способами: таблицей, аналитически, графически.

2. Предел функции

Для функции двух и более числа переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек плоскости, координаты которых удовлетворяют неравенству , называется – окрестностью точки . Другими словами, – окрестностью точки – это все внутренние точки круга с центром и радиусом .

Пусть функция определена в некоторой окрестности точки , кроме, быть может, самой этой точки. Число называется пределом функции при (или, что то же самое, при ), если для любого существует такое, что для всех и удовлетворяющих неравенству выполняется неравенство . Записывают:

.

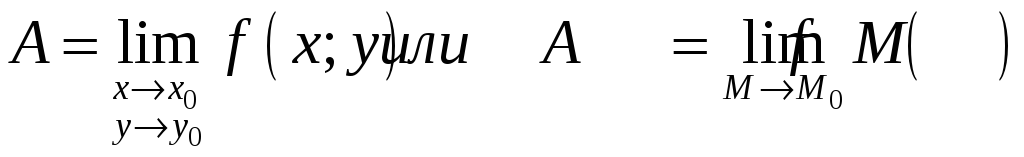Из определения следует, что если предел существует, то он не зависит от пути, по которому стремится к (число таких направлений бесконечно; для функции одной переменной по двум направлениям: слева и справа!).

Геометрически смысл предела функции двух переменных состоит в следующем. Каково бы ни было число , найдется - окрестность точки , что во всех её точках , отличных от точки , аппликаты соответствующих точек поверхности отличаются от числа по модулю меньше, чем на .

Пример

Найти предел .

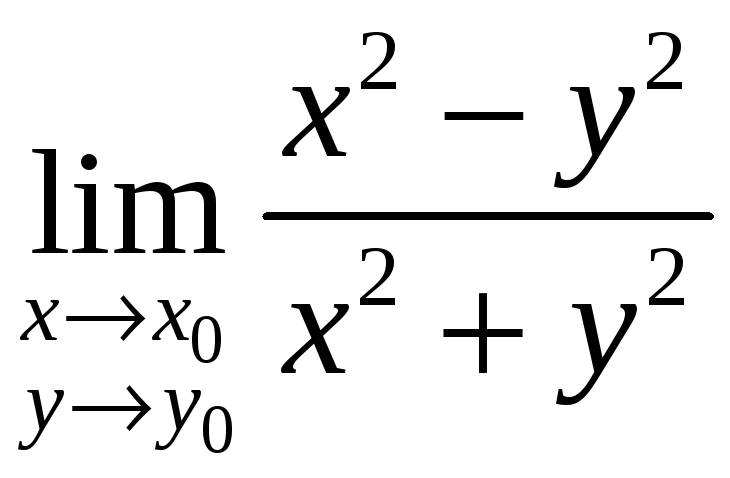Решение: Будем приближаться к по прямой , где – некоторое число. Тогда

.

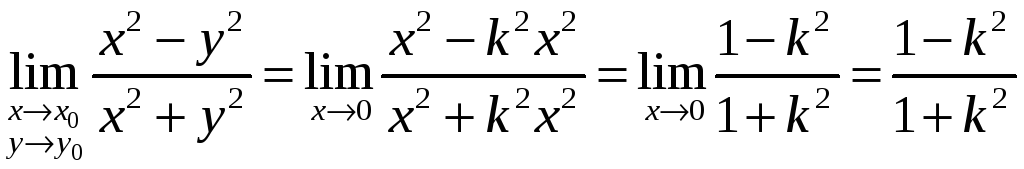Функция в точке предела не имеет, так как при разных значениях предел не одинаков (функция имеет различные значения)

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной. Это означает, что справедливы утверждения:

если функции определены на множестве и имеют в точке этого множества пределы соответственно, то и функции 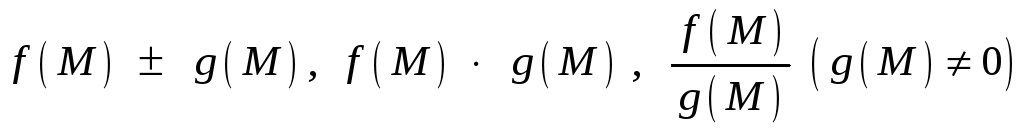имеют в точке пределы, которые соответственно равны .

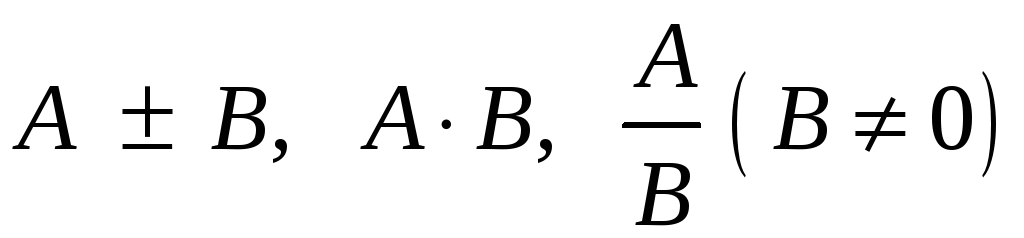1.3 Непрерывность функции двух переменных

Функция () называется непрерывной в точке , если она:

а) определена в этой точке и некоторой ее окрестности,

б) имеет предел

в) этот предел равен значению функции в точке , т.е.

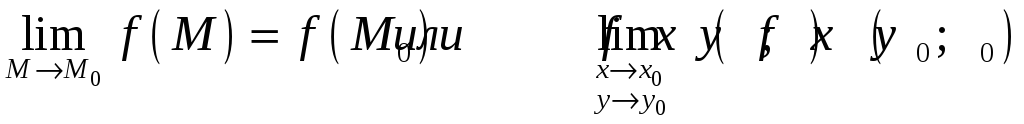
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва могут образовывать целые линии разрыва или поверхности разрыва. Так, функция имеет линию разрыва . Можно дать другое, равносильное определение непрерывности функции в точке. Обозначим , Величины и называются приращениями аргументов и , а – полным приращением функции в точке .

Функция называется непрерывной в точке , если выполняется равенство , т.е. полное приращение функции в этой точке стремится к нулю, когда приращения её аргументов и стремятся к нулю.

Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям – подобные теоремы имели место для функций одной переменной.

1.4 Свойства функций, непрерывных в ограниченной замкнутой области

Приведем свойства функций непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной). Предварительно уточним понятие области.

Областью называется множество точек плоскости, обладающих свойством открытости и связности.

Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.

Свойство связности: любые две точки этой области можно соединить непрерывной линией, целиком лежащей в этой области.

Точка называется граничной точкой области , если она не принадлежит , но в любой окрестности лежат точки этой области. Совокупность граничных точек области называется границей . Области с присоединенной к ней границей называется замкнутой областью, обозначается, обозначается . Область называется ограниченной, если все её точки принадлежат некоторому кругу радиуса . В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координатного угла, а примером ограниченной – - окрестность точки.

Теорема 1.1. Если Функция непрерывна в ограниченной замкнутой области, то она в этой области:

а) ограничена, т.е. существует число , что для всех точек в этой области выполняется неравенство ;

б) имеет точки, в которых принимает наименьшее и наибольшее значения;

г) принимает хотя бы в одной точке области любое численное значение. Заключенное между и .

Теорема дается без доказательмтва.