3.29 Сравнение нескольких дисперсий нормальных генеральных совокупностей по выборкам одинакового объема. Критерий Кочрена

Пусть генеральные совокупности Х1, Х2, .... Хi распределены нормально. Из этих совокупностей из- влечено l независимых выборок одинакового объе- ма л и по ним найдены исправленные выборочные дис- персии 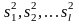, все с одинаковым числом степеней

свободы к = n — 1.

Требуется по исправленным дисперсиям при заданном уровне значимости а проверить нулевую гипотезу, со­стоящую в том, что генеральные дисперсии рассматрива­емых совокупностей равны между собой: H0=D(X1)=D(X2)=D(Xl). Другими словами, требуется проверить, значимо или незначимо различаются исправленные выборочные дис­персии.

Итак, в качестве критерия проверки нулевой гипо­тезы примем критерий Кочрена—отношение максималь­ной исправленной дисперсии к сумме всех исправленных дисперсий:

.

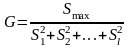Распределение этой случайной величины зависит только от числа степеней свободы к = n— 1 и количества выбо­рок I.

Критическую область строят правостороннюю, исходя из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости: P[G>Gкр(xkl)]=a

Критическую точку Gкр(akl) находят по таблице приложения 8, и тогда правосторонняя критическая об­ласть определяется неравенством G> Gкр, а область при­нятия нулевой гипотезы — неравенством G< Gкр .

Обозначим значение критерия, вычисленное по дан­ным наблюдений, через Gнабл и сформулируем правило проверки нулевой гипотезы.

Правило. Для того чтобы при заданном уровне зна­чимости а проверить гипотезу об однородности диспер­сий нормально распределенных совокупностей, надо вы­числить наблюдаемое значение критерия и по таблице найти критическую точку.

Если Gнабл< Gкр —нет оснований отвергнуть нулевую гипотезу.

Если Gнабл>Gкр — нулевую гипотезу отвергают.

Замечание. Если требуется оценить генеральную дисперсию, то при условии однородности дисперсий целесообразно принять в ка­честве ее оценки среднюю арифметическую исправленных выбороч­ных дисперсий.

3.30 Проверка гипотезы о значимости выборочного коэффициента корреляции

Пусть двумерная генеральная совокупность (X, У) распределена нормально. Из этой совокупности из­влечена выборка объема n и по ней найден выборочный коэффициент корреляции 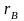, который оказался отличным от нуля. Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генераль­ной совокупности 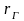также отличен от нуля. В конечном счете нас интересует именно этот коэффициент, поэтому возникает необходимость при заданном уровне значи­мости а проверить нулевую гипотезу Н0:rг = 0 о равен­стве нулю генерального коэффициента корреляции при конкурирующей гипотезе .

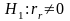Если нулевая гипотеза отвергается, то это означает, что выборочный коэффициент корреляции значимо отли­чается от нуля (кратко говоря, значим), а X и У корре­лированы, т. е. связаны линейной зависимостью. Если нулевая гипотеза будет принята, то выбо­рочный коэффициент корреляции незначим, а X и У не-коррелированы, т. е. не связаны линейной зависимостью.

В качестве критерия проверки нулевой гипотезы при­мем случайную величину

.

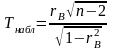Величина Т при справедливости нулевой гипотезы имеет распределение Стьюдента с к=n - 2 степенями свободы.

Обозначим значение критерия, вычисленное по дан­ным наблюдений, через Тнабл и сформулируем правило проверки нулевой гипотезы.

Правило. Для того чтобы при заданном уровне зна­чимости а проверить нулевую гипотезу Н0:rг = 0 о ра­венстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конку­рирующей гипотезе , надо вычислить наблюда­емое значение критерия:

и по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней сво­боды к = n- 2 найти критическую точку 1Ю (а; к) для двусторонней критической области.

Если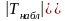 —нет оснований отвергнуть нуле­вую гипотезу.

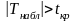Если —нулевую гипотезу отвергают.

3.31 Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.Проверка гипотезы о предполагаемом законе неизвестного распределения производиться при критерии согласия. КС-критерий проверки гипотезы о предполагаемом законе неизв-го распределения. Будем сравнивать эмпирические и теоретические частоты. Случайно ли расхождение частот? Критерий Пирсона отвечает на поставленный выше вопрос. Он не доказывает справ-сть гипотезы, а лишь устанавливает на принятом уровне значимость ее согласия или несогласия с данными наблюдений. Для того, чтобы при заданном уровне значимости проверить 0-ю гипотезу H₀: ген-я сов-сть распределена нормально, надо сначала вычислить теоретич. частоты, а затем наблюд. значения крит.: Х_набл. ² =Ε(ni-ńi)²/ni. И по таблице критических точек распределения. Если Х_набл. ² <X_кр.² - нет оснований отвергнуть нулевую гипотезу. Если Х_набл. ² >X_кр.² -нул. Гипотезу отвергают.

3.32 Выборочный коэффициент ранговой корреляции Спирмена и проверка гипотезы о его значимости.Для оценки степени связи признаков вводят коэффициент ранговой корреляции(р.к.) Спирмена. Для практических целей исп-е р.к. весьма полезно. Рассмотрим 2 крайних случая:1) Ранги по признакам А и В совпадают при всех значениях индекса i: Xi=Yi. В этом случае ухудшение качества по одному признаку влечет ухудшение качества по другому. Признаки связаны: имеет место «полная прямая зависимость».2)Ранги по признакам А и В противоположны в том смысле. что если X1=1,то Y1=n; если Х2=2, то У2=n-1….. В этом случае ухудшение кач-ва по одному признаку влечет улучшение кач-ва по другому. Призн. Связ.: имеет место «противоположная зь между призраками. О связи между качеств-ми признаками Аи В можно судить по связи м-ду случ. велич. Х и У, для оценки кот-й использ-ся коэф. Коррел. Формула: r_в = Εu_iv_i /nσ_uσ_v.Выборочный к-т р.к. Спирмена: р_в=1-[(6Εd_i²)/(n³-n)]. Св-ва коэф-та коррел. Спирмена:1) Если между качественными признаками А и В имеется «полная прямая зависимость» в том смысле, что ранги объектов совп-т при всех значениях i, то к-т Спирмена равен единице. Р_в=1. 2)Если м-ду кач-ми призн-ми А и В имеется ” противоположная зависимость в том смысле, что рангу х₁=1 соотв-т рангу у₁=n,…, х_n=n соотв. Ранг у_n=1., то к-т Спирмена равен минус единице. Р_в=-1. 3) Если между качественными признаками А и В нет ни ”полной прямой”, ни “противоположной” зависимостей, то к-т заключен м-ду -1 и +1, причем чем ближе к 0 его абсолютная величина, тем зависимость меньше. Правило: для того чтобы при уровне значимости α проверить нулевую гипот. О рав-ве 0 генерального к-та р.к.Спирмена, надо вычислить критич-ю точку: Т_кр =t_кр(α;к)√(1-р_в²)/(n-2), Где n- объем выб-ки, р_в- выб-й к-т корр.Спирмена, t_кр(α;к )-крит. Точка крит. Области, кот. Находят по таблице. Если │р_в│< Т_кр -нет оснований отвергнуть нул. Гипотезу. Ранговая корр. Связь незначима. Если│р_в│> Т_кр - нул. Гипот. Отвергают. Сущ-т значимая связь.

3.33. Связь м-ду двумя кач-ми признаками оценивают т-же, используя к-т ранговой коррел. Кендалла. Пусть ранги объектов выб-ки: по признаку А х₁, х₂,…,х_n, по призн. В у₁,у₂,…,у_n.Выборочный к-т ранговой корр. Кендалла опр-ся ф-лой: Т_В=[4R/n(n-1)]-1, где n-объем выб-ки. Св-ва: 1. В случае«полной прямой зависимости» признаков: х1=1,х2=2,…,хn=n; у1=1,у2=2,…,уn=n. 2.В случае “противоположной” зависимости х1=1,х2=2,…,хn=n; у1=n,у2=n-1,...,уn=1. Правило, позволяющее установить значимость или незначимость ранговой связи Кендалла: для того чтобы при уровне значимости α проверить нулевую гипот. О рав-ве 0 генерального к-та р.к.Кендалла, надо вычислить критич-ю точку: Ткр =Z_кр√[2(2n+5)]/ [9n(n-1)], где n - объем выб-ки, Z_кр -крит.точка крит. Области. Если │т_в│< Т_кр - нет оснований отвергнуть нул. Гипотезу. Ранговая корр. Связь незначима. Если │т_в│> Т_кр -нул. Гипот. Отвергают. Сущ-т значимая связь.

3.34. Критерий Вилкоксона служит для проверки однородности двух независимых выборок: х1,х2,…,хn и у1,у2,…,уn. Этот крит. Применим к случайным величинам, распр-я кот-х неизвестны; треб-ся лишь, чтобы величины были непрерывными.

А.Проверка нул. Гипот. В случае , если объем обеих выб-к не превосходит 25. Правило1.: Для того чтобы при заданном уровне значим. а=2Q проверить нул. Гипот. Об однородности двух незав-х выб-к объемов n₁ и n₂ ,надо:1).расположить варианты обеих выб-к в возрастающем порядке, т.е в виде одного вариационного ряда, и найти в этом ряду наблюдаемое значение критерия W_набл – сумму порядковых номеров вариант первой выб-ки; 2) найти по таблице нижнюю крит. Точку W_{нижн. Кр} n1- W_{нижн. Кр}, где Q=α/2; 3)найти верхнюю крит. Точку по ф-ле: W _{верхн. Кр} =(n1+n2+1)n1- W_{нижн. Кр} Если W_набл< W_{нижн. Кр} или W_набл > W _{верхн. Кр} -нул. Гипот. Отвергают. Если W_{нижн. Кр} <W_набл <W _{верхн. Кр} - нет оснований отвергнуть нул. Гипотезу. Правило 2: Надо анйти по табл. Нижн. Крит. Точку W_{нижн. Кр} (Q;n₁,n₂), где Q=α. Если W_набл > W_{нижн. Кр} -нет оснований отвергнуть нул. Гипот. Если W_набл > W _{верхн. Кр} -нул. Гипот. Отвергают. Правило3: Надо найти верхн. Крит. Точку: W _{верхн. Кр} (Q;n₁,n₂) =(n1+n2+1) n1- W_{нижн. Кр} n1- W_{нижн. Кр} (Q;n₁,n₂), где Q=α. Если W_набл < W _{верхн. Кр -}нет оснований отвергнуть нул. Гипот. Если W_набл > W _{верхн. Кр} -нул. Гипот. Отвергают.

Б. Проверка нул. Гипот. В случае , если объем хотя бы одной из выб-к превосходит 25.

1. Нижняя крит. Точка: W_{нижн. Кр} (Q;n₁,n₂) =[ (n1+n2+1) n1-1/2 - Z_кр √n1n2 (n1+n2+1) /12], где Q=α/2; Z_кр находят пот таблице функции Лапласа.

2. Нижняя крит. Точку находят по ф-ле, что и в пункте 1, положив Q=α; соотв-но Z_кр находят пот таблице функции Лапласа. Остальные правила сохран-ся.