27. Расчёт цилиндрических винтовых пружин малого шага.

Определим напряжения и деформации при осевом растяжении и сжатии цилиндрической пружины, навитой из прутка круглого сечения диаметра d. Конструктивно пружины растяжения и сжатия отличаются оформлением их концов, но концевые витки при расчетах пружин на прочность и жесткость во внимание не принимаются.

Цилиндрические пружины характеризуются средним диаметром витка D, числом витков n, углом подъема витков α и шагом пружины h.

Наибольшее распространение в технике имеют пружины с небольшим углом подъема винтовой линии (α<5°), называемые пружинами малого шага.

В пружинах малого шага можно пренебречь подъемом витков и считать длину витка примерно равной πD, а сам виток - расположенным в плоскости, нормальной к оси пружины. Но в таком случае, сечение прутка пружины плоскостью, содержащей ее ось, можно рассматривать как ее поперечное сечение. Указанные допущения положены в основу приближенного расчета пружин.

Разделим пружину осевым сечением на две части и отбросим, одну из них. Из условия равновесия оставшейся части следует, что внутренние касательные силы упругости в сечении пружины приводятся к перерезывающей силе Q=P и крутящему моменту Мк=PD/2.

Касательные напряжения, вызванные кручением, достигают максимума в контурных точках сечения, а напряжения от перерезывающей силы можно в первом приближении считать равномерно распределенными по плоскости сечения.

Или

Для большинства пружин отношение d/2D - величина малая по сравнению с единицей. Это говорит о том, что основным видом деформации для пружин является кручение, а срезом можно пренебречь и вычислять напряжения в пружине по формуле

Изменение продольных размеров λ удобно определить энергетическим методом, приравнивая работу А статически приложенной силы Р потенциальной энергии деформации U пружины. Работа внешних сил A=Pλ/2, а потенциальная энергия накапливается, главным образом, за счет кручения прутка и поэтому может быть вычислена по формуле. Учитывая, что крутящий Мк=PD/2 и момент инерции Ip=πd4/32 по длине прутка не изменяются, а длина прутка l = πdn, получаем

Приравнивая A и U, находим

28. Статически неопределимые задачи при кручении.

При кручении, как и при растяжении, могут встретиться статически неопределимые задачи, для решения которых к уравнениям равновесия статики должны быть добавлены уравнения совместности перемещений.

Метод решения указанных задач при кручении и при растяжении один и тот же. Рассмотрим для примера брус, заделанный обоими концами в абсолютно жесткие стены. Отбросим заделки, заменив их действие неизвестными моментом M1 и M2. Уравнение совместности деформаций получим из условия равенства нулю угла закручивания в правой заделке:

Крутящие моменты в сечениях бруса связаны следующим уравнением:

Решаем совместно указанные уравнения относительно неизвестных моментов.

Угол закручивания сечения C определяется из уравнения

29. Внутренние силовые факторы при изгибе бруса.

При заданном значении внешних нагрузок (F, М, q) величины реакций в опорах находят из условия статики равновесия системы: сумма проекций всех сил на координатные оси и сумма моментов всех сил относительно любой точки бруса равны нулю. При этом распределенную нагрузку по длине какого-либо участка бруса заменяют сосредоточенной силой, приложенной в центре тяжести эпюры, определяющей характер ее распределения (интенсивность q). Например, для схемы нагружения бруса реакции опор находят из условий:

Для определения внутренних силовых факторов используют метод сечений. С этой целью в исследуемом поперечном сечении, определяемом координатой z, брус мысленно рассекается на две части, одна из которых «отбрасывается». Действие отсеченной части заменяется внутренними силовыми факторами, которые являются равнодействующими напряжений по всему поперечному сечению:

,

,

Границами участков являются пределы действия распределенных нагрузок и точки приложения внешних сил и моментов.

30. Дифференциальные зависимости между силовыми факторами при изгибе.

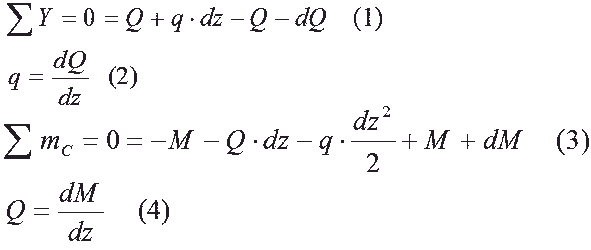
31. Правила построения эпюр поперечных сил и изгибающих моментов.

В сечениях балок, загруженных вертикальными нагрузками, возникают, как правило, два внутренних силовых фактора - поперечная сила Qy и изгибающий момент Mx .

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Правило знаков для Qy: условимся считать поперечную силу в сечении положительной, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде

Изгибающий момент Mx в сечении численно равен алгебраической сумме моментов внешних сил, приложенных по одну сторону от рассматриваемого сечения, относительно оси x , проходящей через данное сечение.

Правило знаков для Mx: условимся считать изгибающий момент в сечении положительным, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, приводит к растяжению в данном сечении нижних волокон балки и отрицательной - в противном случае.

Схематически это правило знаков можно представить в виде:

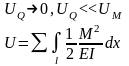
36. Потенциальная энергия деформации при изгибе.

Полная потенциальная энергия упругого деформирования состоит из потенц. энергии момента и поперечной силы: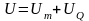

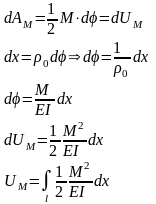
Выделим элемент тела 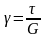- угловая деформация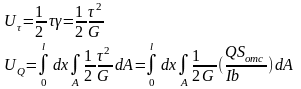

35. Напряжения при изгибе тонкостенных балок. Центр изгиба.

Центр изгиба - точка поперечного сечения бруса, такая, что брус при изгибе не испытывает кручения, если поперечная сила проходит через центр изгиба. В упругом брусе положение центр изгиба не зависит от величины силы. Определение центра изгиба важно для расчёта ряда конструкций. Например, чтобы крыло самолёта в полёте не изменяло самопроизвольно угол атаки, надо профиль крыла выбрать такой, чтобы подъёмная сила проходила через центр изгиба.

34. Расчёты на прочность при поперечном изгибе.

При попер. изгибе наиб. норм. напряжения возникают в наиб. удаленных от нейтральной оси точках сечения, а на самой этой оси норм. напряжения = 0, тогда как зона действия наиб. касательных напряжений расположена, наоборот, вблизи нейтральной оси. Кроме того, величина τmax мала по сравнению с σmax, если длина балки существенно больше высоты сечения. Все это позволяет не принимать во внимание касательные напряжения и проводить расчет на прочность только по норм. Напряжениям.

Условие прочности балки требует, чтобы максимальные нормальные напряжения не превышали допускаемых напряжений для материала балки:

Если материал одинаково работает на растяжение и сжатие, то опасной будет та точка сечения, где действует наибольшее по абсолютной величине напряжение независимо от его знака. Для хрупких материалов, имеющих существенно различные пределы прочности при растяжении 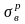и сжатии 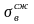, требуется проверка прочности по наибольшим растягивающим и сжимающим напряжениям:

,

Для балок из пластичных материалов, одинаково работающих на растяжение и сжатие, целесообразно выбирать сечения, симметричные относительно их нейтральных осей; при этом условии обеспечивается одинаковый запас прочности сечения по растянутым и сжатым волокнам.

33. Касательные напряжения при поперечном изгибе. Формула Журавского.

При поперечном изгибе кроме нормальных напряжений в поперечном сечении бруса возникают касательные напряжения, а согласно закону парности, такие же напряжения появляются и в продольных сечениях бруса.

Касательное напряжение в любой точке поперечного сечения определяется, как и парное напряжение, возникающее в продольном сечении, по формуле Журавского;

где Qy - поперечная сила в рассматриваемом сечении;

Sy отс- статический момент относительно нейтральной оси поперечного сечения той его части, которая расположена по одну сторону от прямой KL, проведенной параллельно нейтральной оси через исследуемую точку;

b - ширина поперечного сечения на уровне исследуемой точки;

Jz - момент инерции всего сечения относительно нейтральной оси.

В основу вывода формулы Журавского положено допущение о равномерном распределении касательных напряжений по ширине сечения.

В балке прямоугольного и круглого сечений максимальные касательные напряжения возникают в тех точках, где нормальные напряжения равны нулю (на нейтральной оси), и, наоборот, в крайних точках сечения, где нормальные напряжения максимальны, касательные напряжения равны нулю. Поэтому за опасные можно принять точки, наиболее удаленные от нейтральной оси, что подтверждается практикой эксплуатации балок, работающих на изгиб.

32. Нормальные напряжения при чистом изгибе. Рациональные формы поперечных сечений балок.

Нормальные напряжения зависят только от изгибающих моментов, поэтому вывод формулы для вычисления σ можно производить применительно к чистому изгибу, при котором во всех сечениях Q=0, Mz=const.

Для определения нормальных напряжений необходимо знать положение нейтрального слоя, то есть ρ. Для этого рассмотрим условия равновесия между нагрузочным моментом, действующим на какое-нибудь симметричное сечение F и внутренними силами σdF, распределенными по этому сечению.

Формулы для определения напряжений и кривизны балки применимы и для поперечного изгиба:

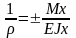
37. Перемещения при изгибе. Диф. Ур. Упругой линии и его интегрирование.

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси. Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.

Между прогибами y(x) и углами поворота сечений θ(x) существует определенная зависимость.

Угол поворота сечения θ равен углу φ наклона касательной к упругой линии.

Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента Mz и жесткости EIz

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

Это равенство называется дифференциальным уравнением упругой линии.

Интегрируя, находим сначала углы поворота сечений:

А после второго интегрирования – прогибы балки:

38. Перемещения при изгибе. Метод начальных параметров.

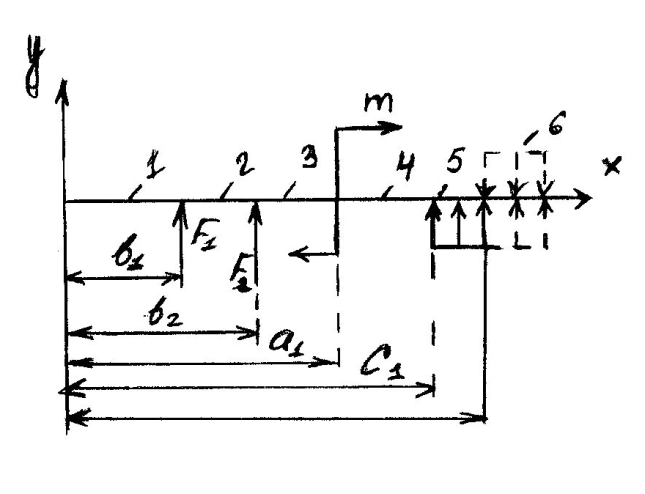
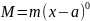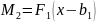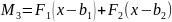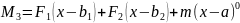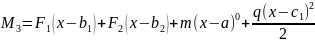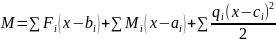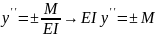В методе начальных параметров начало координат всегда располагается в левом конце балки. Если распределённая нагрузка обрывается, то ее продляют до конца балки и вводят компенсирующую нагрузку. При записи момента его привязывают к точке . , , , , , тогда . , тогда 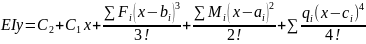; из н.у. 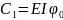, , тогда получим прогиб: 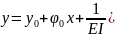) ; углы поворота: .

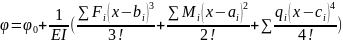39. Энергетический метод определения перемещений сечений балок. Интеграл Мора.

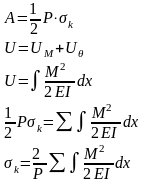
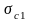– перемещение точки с под действием силы = 1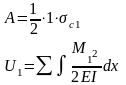

Под единичной нагрузкой балка прогнулась, приложили силу Р.

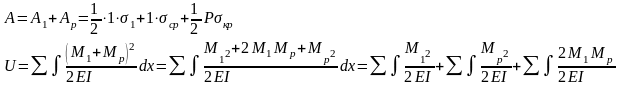
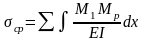- интеграл Мора

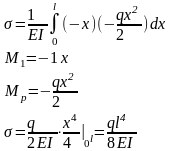
В той точке, где ищем перемещение, прикладываем единичную нагрузку, находим M₁ и M_p. Подставляем в интеграл Мора.

40. Способ Верещагина. Формула Симпсона.

Верещагин предложил простой графоаналитический прием вычисления интеграла Мора в случаях, когда эпюра Mz1 (или Mz) ограничена прямыми линиями. Это прием графоаналитического вычисления определенного интеграла от произведения двух функций f(x) и φ(x), из которых одна, например φ(x), линейная, т. е. имеет вид

Рассмотрим участок балки, в пределах которого эпюра изгибающих моментов от единичной нагрузки ограничена одной прямой линией Mz1=kx+b, а изгибающий момент от заданной нагрузки изменяется по некоторому произвольному закону Mz. Тогда в пределах этого участка

Второй интеграл представляет собой площадь ω эпюры Mz на рассматриваемом участке, а первый - статический момент этой площади относительно оси y и поэтому равен произведению площади ω на координату ее центра тяжести xc. Таким образом,

По способу Верещагина операция интегрирования заменяется перемножением площади ω одной эпюры на ординату yc второй (обязательно линейной) эпюры, взятой под центром тяжести площади ω.

Формула Симпсона относится к приёмам численного интегрирования.

Суть приёма заключается в приближении подынтегральной функции на отрезке [a,b] интерполяционным многочленом второй степени , то есть приближение графика функции на отрезке параболой.

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке [a,b]:

где f(a), f((a + b) / 2) и f(b) — значения функции в соответствующих точках (на концах отрезка и в его середине).