22. Деформации при кручении цилиндрического бруса круглого сечения.

Выделим из круглого бруса маль: элемент длиной dz. В нем, в свою очередь, двумя цилиндрическим поверхностями с радиусами р и р + dр вырежем элементарное колы (рис. 3.9, а), что позволит считать напряжения равномерно распределенными по кольцевому сечению. Предположим, что в процессе деформирования правое сечение кол! ца повернулось относительно левого на угол 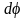. Мерой деформаци кручения является относительный угол закручивания -угол закручивания, приходящийся на единицу длины, 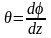, где dz — расстояние между сечениями, которые поворачиваются отнс сительно друг друга на . Величина 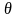играет при кручении такую ж( роль, как относительное удлинение при растяжении.

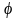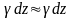Однако к деформации кручения можно подойти и с другой стороны. При закручивании рассматриваемого цилиндра образующие ас и bd перемещаются в положения ас' и bd', а радиусы Ос и Оd — в положе­ния Ос' и Оd’ . В результате этого бесконечно малый элемент боковой поверхности аbdс претерпевает чистый сдвиг. С одной стороны, cc¹ = рd , так как cc¹ — дуга окружности, с дру­гой стороны, cc' =tg , так как cc' — полный сдвиг.

Приравнивая эти значения, имеем

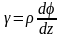
Угол гама представляет собой угол сдвига. С учетом ;

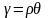
23. Потенциальная энергия деформации при кручении.

Потенциальная энергия деформации при кручении определяется подобно тому, как это делалось при растяжении и сдвиге.

Удельная потенциальная энергия деформации при чистом сдвиге определяется из уравнения

Потенциальная энергия деформации U определится из уравнения путем интегрирования по объему:

При этом учитывалось, что

В брусе постоянной жесткости GIp при действии постоянного по длине крутящего момента, имеем

24. Кручение тонкостенного бруса замкнутого профиля.

Брус считается тонкостенным, если толщина стенки существенно меньше его прочих линейных размеров.

При кручении тонкостенного бруса его поперечные сечения депланируют. Если ничто не препятствует свободной депланации сечений, кручение называется чистым или свободным. В противном случае кручение называется стесненным. При стесненном кручении, в отличие от свободного, в поперечных сечениях кроме касательных напряжений возникают также и нормальные напряжения.

Рассмотрим случай свободного кручения тонкостенного бруса замкнутого контура, при котором поперечные сечения могут свободно депланировать, но не искажаться в своей плоскости, т. е. не изменяется форма сечения в плане.

В случае кручения замкнутых тонкостенных профилей обычно считают, что толщина стенки настолько мала, что касательные напряжения по толщине стенки можно принять одинаковыми и равными напряжениям посредине толщины стенки и направленными по касательной к срединной линии толщины стенки. Составляя сумму проекций всех сил, приложенных к элементу, вырезанному из профиля, на ось профиля x, получим

Т.е. произведение касательных напряжений на толщину стенки, или поток касательных напряжений вдоль контура сечения, постоянен

25. Распределение напряжений по сечению при кручении бруса прямоугольного сечения.

Опыт показывает, что при кручении бруса любого некруглого сечения его поперечные сечения искривляются (депланируют). Это обстоятельство значительно усложняет задачу определения напряжений и деформаций, так как не позволяет принять гипотезу плоских сечений. Поэтому задачи кручения брусьев некруглых сечений могут быть решены только методами теории упругости. Точки наиболее удаленные от центра сечения, имеют наибольшие перемещения и, следовательно, в них должны действовать наибольшие напряжения. Например, в брусе прямоугольного сечения τmax должны были бы возникнуть в угловых точках. Но опыт показал, что на самом деле именно в этих точках касательные напряжения равны нулю. Если бы на площадке поперечного сечения в угловой точке действовало напряжение, то его можно было бы всегда разложить на составляющие, направленные вдоль сторон прямоугольника. Каждая из этих составляющих должна быть равна нулю, так как парные им напряжения на свободной от продольной касательной нагрузки боковой поверхности бруса равны нулю. Следовательно, и напряжение τ=0.

Решение задачи о кручении бруса прямоугольного сечения полученное в теории упругости Сен-Венаном, показывает, что касательные напряжения в контурных точках сечения возрастают от нулевых значений в углах к серединам сторон по некоторым кривым; в центре сечения напряжение равно нулю, а максимального значения напряжения достигают в серединах длинных сторон, причем

Наибольшее напряжение на короткой стороне прямоугольника

Угол закручивания определяется по формуле

Где

,

В этих формулах b - длина короткой стороны; h - длинной сторону прямоугольника; α, β, γ - числовые коэффициенты, зависящие от соотношения сторон h и b.

26. Расчёты на прочность и жёсткость при кручении.

Принципы расчетов на прочность полностью справедливы и для случая кручения бруса. При кручении расчеты на прочность также делятся на проектировочные и поверочные. В основе расчетов лежит условие прочности

где τmax - максимальное касательное напряжение в брусе, определяемое по вышеприведенным уравнениям в зависимости от формы сечения; [τ] - допускаемое касательное напряжение, равное части предельного напряжения для материала детали - предела прочности τв или предела текучести τт. Коэффициент запаса прочности устанавливается из тех же соображений, что и при растяжении. Например, для вала полого круглого поперечного сечения, с внешним диаметром D и внутренним диаметром d, имеем

где α=d/D - коэффициент полости сечения.

Условие жесткости такого вала при кручении имеет следующий вид:

где [φo] - допускаемый относительный угол закручивания.

31

32

33