
- •§1. Раскрытие неопределенностей с помощью правила Лопиталя. Формулировка правила Лопиталя.
- •Раскрытие неопределенностей или .
- •§2. Возрастание и убывание функции.
- •§3. Экстремумы функции.
- •§4. Наибольшее и наименьшее значения функции.
- •§5. Выпуклость и вогнутость графика функции. Точки перегиба.
- •§6. Асимптоты плоской кривой.
- •§7. Полное исследование функции и построение графика.
§6. Асимптоты плоской кривой.
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Для кривой, которая
является графиком функции
![]() ,
различают вертикальные, наклонные и
горизонтальные асимптоты.
,
различают вертикальные, наклонные и
горизонтальные асимптоты.
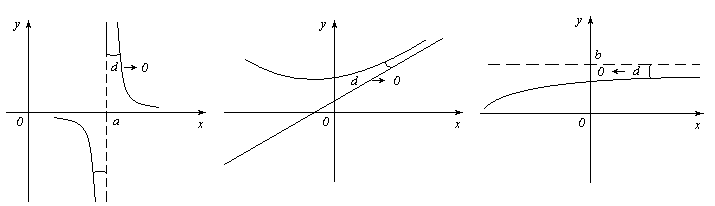
Прямая х = а
является вертикальной асимптотой
графика функции
![]() ,
если выполняется хотя бы одно из условий:
,
если выполняется хотя бы одно из условий:
![]() или
или
![]() ,
т.е.
,
т.е.
если значение х = а является точкой бесконечного разрыва функции или границей ее области определения.
Прямая
![]() является наклонной (при k = 0
горизонтальной) асимптотой
графика функции
является наклонной (при k = 0
горизонтальной) асимптотой
графика функции
![]() ,
если существуют конечные пределы
,
если существуют конечные пределы
![]() ,
и
,
и
![]() . (1)
. (1)
Если хотя бы один из
этих пределов не существует и равен
бесконечности, то кривая
![]() наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
При вычислении, пределы (1) могут быть различными при х и при х–.
Пример 1.
Найти асимптоты графика
функции
![]() .
.
Решение.
Область определения функции: х 3, поэтому х = 3 является точкой разрыва функции.
Вычисляем
![]()
![]() и заключаем, что прямая х = 3
является вертикальной асимптотой
графика.
и заключаем, что прямая х = 3
является вертикальной асимптотой
графика.
Наклонные (горизонтальные)
асимптоты ищем уравнением
![]() ,
в котором числа k и b вычисляем
по формулам (1):
,
в котором числа k и b вычисляем
по формулам (1):
![]()
![]() =
=![]() ,
,
![]()
![]()
![]() =
=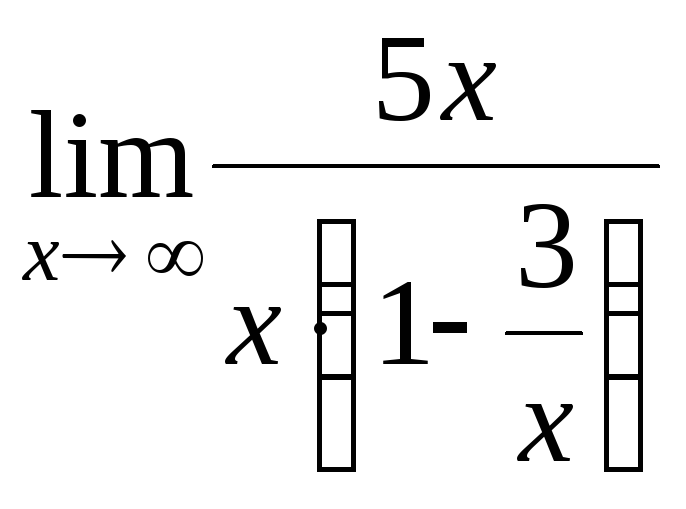
![]() .
.
Таким образом, график
функции
![]() имеет две асимптоты: вертикальную х = 3
и горизонтальную y = 5
при х.
имеет две асимптоты: вертикальную х = 3
и горизонтальную y = 5
при х.
Ответ: х = 3, y = 5.
Пример 2.
Найти асимптоты графика
функции
![]() .
.
Решение.
Область определения функции: х 1 х = 1 – точка разрыва графика.
Так как
![]()
![]() ,
то прямая х = 1 является
вертикальной асимптотой. Наклонные
(горизонтальные) асимптоты:
,
то прямая х = 1 является
вертикальной асимптотой. Наклонные
(горизонтальные) асимптоты:
![]() ,
где
,
где
![]()
![]() 3,
3,
![]()
![]()
![]()
![]() 3
3
y = 3x + 3 – наклонная асимптота.
Ответ: х = 1, y = 3x + 3.
Пример 3.
Найти асимптоты графика
функции
![]() .
.
Решение.
Область определения функции: х > 0.
На границе области определения возможна вертикальная асимптота.
Вычисляем
![]() и заключаем, что прямая х = 0
является правосторонней вертикальной
асимптотой.
и заключаем, что прямая х = 0
является правосторонней вертикальной
асимптотой.
Наклонные (горизонтальные)
асимптоты:
![]() ,
,
где
![]()
![]() =
=![]()
![]() =1,
=1,
![]()
![]()
наклонных асимптот нет.
Ответ: х = 0 при х +0.
Пример 4.
Найти асимптоты графика
функции
![]() .
.
Решение.
Область определения функции: х 1.
Т.к.
![]()
![]()
![]() ,
то прямая х = 1 является
вертикальной асимптотой графика
(двухсторонней).
,
то прямая х = 1 является
вертикальной асимптотой графика
(двухсторонней).
Наклонные асимптоты:
![]() ,
причем пределы (1) для вычисления чисел
k и b нужно
вычислять отдельно при х +
и х ,
имея в виду поведение функции
,
причем пределы (1) для вычисления чисел
k и b нужно
вычислять отдельно при х +
и х ,
имея в виду поведение функции
![]()
![]() .
.
![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
при х наклонных (горизонтальных) асимптот нет.
![]()
![]() 0,
0,
![]()
![]() 0
0
y = 0 – горизонтальная асимптота только при х .
Ответ: х = 1, y = 0 (при х ).
Дополнительные упражнения.
Найти уравнения асимптот графиков следующих функций.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
|
Ответы.
|
1.
|
2.
|
|
3.
|
4.
|
|
5.
|
6.
|
|
7.
|
|
§7. Полное исследование функции и построение графика.
Полное исследование функций и построение их графиков удобно выполнять по следующей схеме.
-
найти область определения функции;
-
выяснить, не является ли функция чётной или нечётной, периодической;
-
исследовать непрерывность, найти точки разрыва и выяснить характер разрывов;
-
найти асимптоты графика функции;
-
исследовать монотонность функции и найти ее экстремумы;
-
найти точки перегиба, установить интервалы выпуклости и вогнутости графика функции;
-
обозначить дополнительные точки графика функции, например, точки его пересечения с осями координат.
Результат каждого пункта должен сразу отражаться на графике и согласовываться с результатами исследования по предыдущим пунктам.
Пример 1.
Провести полное
исследование функции и построить график
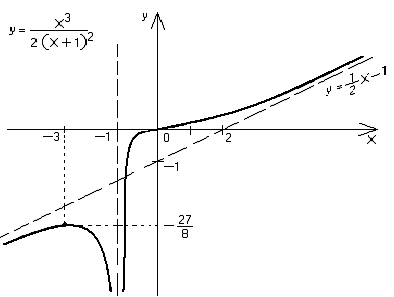
![]() .
.
Решение.
-
Функция определена в интервалах х(–1)(–1;+).
-
Функция не может быть четной или нечетной, т.к. ее область определения не является симметричной относительно 0. Следовательно, данная функция общего вида, т.е. свойством четности не обладает. Также функция не является периодической.
Напомним определения:
Функция
![]() называется четной, если выполняются
два условия:
называется четной, если выполняются
два условия:
-
ее область определения симметрична относительно нуля,
-
для всех значений х из области определения выполняется равенство
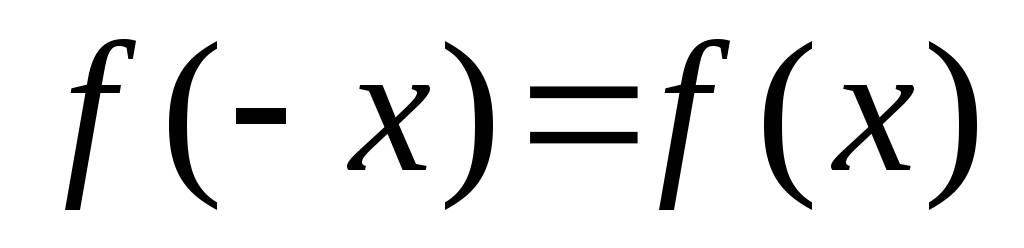 .
.
График четной функции имеет осевую симметрию относительно оси OY.
Функция
![]() называется нечетной, если
называется нечетной, если
-
ее область определения функции симметрична относительно нуля,
-
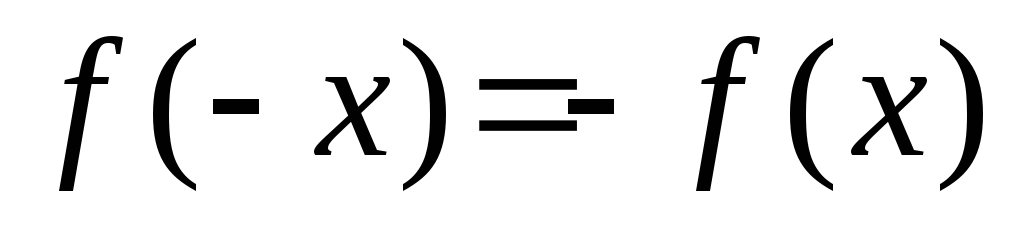 при х из области
определения.
при х из области
определения.
График нечетной функции имеет центральную симметрию относительно начала координат.
Функция называется
периодической, если существует
число Т > 0,
такое что выполняется равенство
![]() для х из области
определения.
для х из области
определения.
Число Т называется периодом функции, а ее график достаточно построить на любом промежутке длиной Т, а затем периодически продолжить на всю область определения.
-
Функция является непрерывной при всех х(––1)(–1;+).
Данная функция является
элементарной, которая образована
делением двух непрерывных основных
элементарных функций
![]() и
и
![]() .
Поэтому, по свойствам непрерывных
функций, данная функция непрерывна во
всех точках, в которых она определена.
.
Поэтому, по свойствам непрерывных
функций, данная функция непрерывна во
всех точках, в которых она определена.
Точка х = –1
является точкой разрыва, т.к. в ней данная
функция не определена. Чтобы определить
характер (тип) разрыва, вычислим
![]()
![]() .
Следовательно, при х = –1
функция имеет бесконечный разрыв (разрыв
II рода).
.
Следовательно, при х = –1
функция имеет бесконечный разрыв (разрыв
II рода).
-
Асимптоты графика функции.
Вертикальной асимптотой является прямая х = –1 (это следует из исследования разрыва функции).
Наклонные
асимптоты ищем уравнением
![]() ,
где
,
где
![]()
![]()
![]()
![]() =
=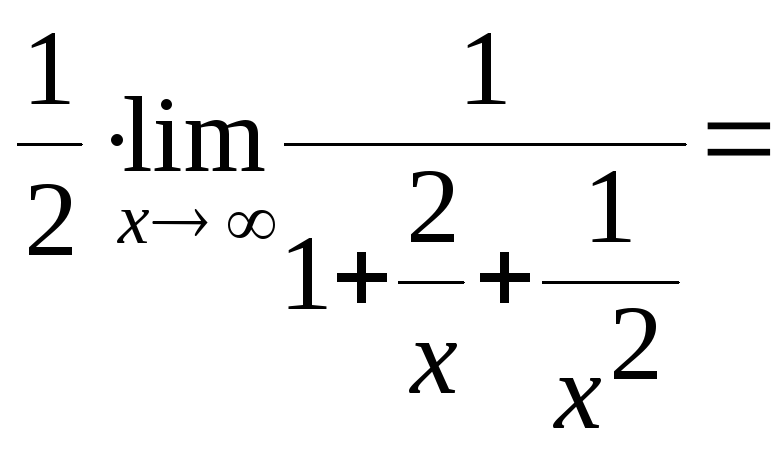
![]() ,
,
![]() =
=![]()
![]()
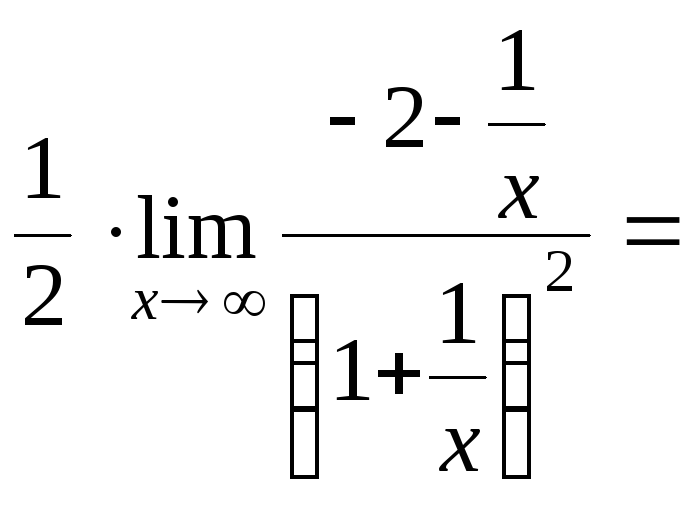
![]() =–1.
=–1.
Таким образом,
![]() – это уравнение наклонной асимптоты
(при х).
– это уравнение наклонной асимптоты
(при х).
-
Монотонность и экстремумы функции определим с помощью ее первой производной:
![]()
![]()
![]()
![]() .
.
Критические точки определяем из условий:
![]()
Достаточные условия монотонности и экстремумов:
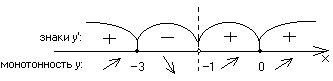
ymax=y(–3)=
![]() .
.
-
Интервалы выпуклости и вогнутости графика функции, ее точки перегиба находим с помощью второй производной:
![]()
![]()
![]()
![]()
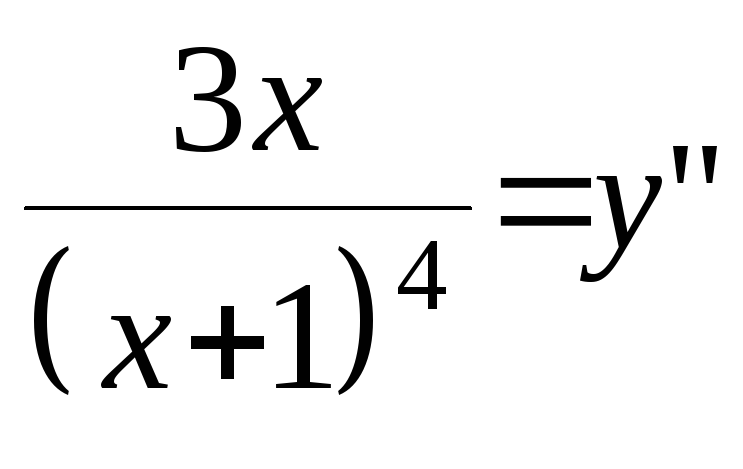 .
.
Подозрительные на перегиб точки определяем из условий:

Достаточные условия выпуклости, вогнутости и точек перегиба:

y(0)=![]() .
.
Точка О(0;0) является точкой перегиба графика.
Часто результаты исследования функции с помощью первой и второй производной оформляют в виде общей таблицы, отражающей основные свойства графика функции:
|
x |
(–3) |
–3 |
(–3;–1) |
–1 |
(–1;0) |
0 |
(0;+) |
|
|
+ |
0 |
– |
не существует |
+ |
0 |
+ |
|
|
– |
– |
– |
не существует |
– |
0 |
+ |
|
|
возрастает, выпуклость |
max |
Убывает, выпуклость |
не существует |
возрастает, выпуклость |
точка перегиба |
возрастает, вогнутость |
Все полученные результаты исследования функции отражаются ее графиком.
Пример 2.
![]() .
.
Решение.
ООФ: х(––![]() )(–
)(–![]() ;
;
![]() )(
)(![]() ;+).
;+).
Функция является нечетной, так как ее область определения симметрична относительно нуля и для хООФ выполняется равенство:
![]()
![]() .
.
Поэтому график функции имеет центральную симметрию относительно начала координат.
Функция является
непрерывной при всех х(––![]() )(–
)(–![]() ;
;
![]() )(
)(![]() ;+),
т.к. элементарная функция непрерывна
на своей ООФ. Точки х=–
;+),
т.к. элементарная функция непрерывна
на своей ООФ. Точки х=–![]() и х=
и х=![]() являются точками бесконечного разрыва,
так как
являются точками бесконечного разрыва,
так как
![]()
![]() ,
,
![]()
![]() .
.
Вертикальными
асимптотами графика являются прямые
х = –![]() и х =
и х = ![]() .
.
Наклонные асимптоты:
![]() ,
где
,
где
![]()
![]()
![]()
 1,
1,
![]() =
=![]()
![]()
![]() =
=![]()
![]() 0.
0.
![]() –
это уравнение наклонной асимптоты.
–
это уравнение наклонной асимптоты.
Интервалы возрастания и убывания функции, ее экстремумы.
![]()
![]()
![]()
![]() .
.
Необходимые условия экстремумов:
![]()
х1 = 0, х2 = 3, х3 = –3 – критические точки.
Достаточные условия монотонности и экстремумов:
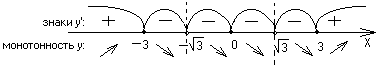
ymax=y(–3)=![]()
![]() ;
;
ymin=y(3)=![]()
![]() .
.
Интервалы выпуклости, вогнутости графика функции и точки перегибов:
![]()
![]()
![]()
![]()
![]()
![]() .
.
Точка х = 0 подозрительная на перегиб.
Достаточные условия:

Точка О(0;0) является точкой перегиба.
Общую таблицу основных свойств графика для данной функции можно составить только для х в следствие центральной симметрии графика относительно точки (0;0):
|
x |
0 |
|
|
|
3 |
(3;+) |
|
|
0 |
– |
не существует |
– |
0 |
+ |
|
|
0 |
– |
не существует |
+ |
+ |
+ |
|
|
точка перегиба |
убывает, выпуклость |
не существует |
убывает, вогнутость |
|
возрастает, вогнутость |
График функции:
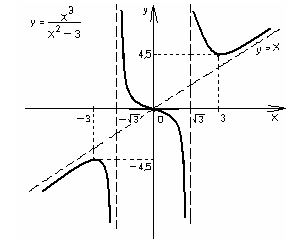
Пример 3.
![]() .
.
Решение.
ООФ: х(–+).
![]()
![]() ,
,
![]()
![]()
![]() .
.
![]()
![]() и
и
![]()
![]() функция свойством
четности не обладает, т.е. не является
ни четной, ни нечетной.
функция свойством
четности не обладает, т.е. не является
ни четной, ни нечетной.
Функция непрерывна при х(–+), точек разрыва нет.
Вертикальных асимптот нет, т.к. нет точек разрыва.
Наклонные асимптоты:
![]() ,
где
,
где
k=![]()
![]()
![]() –1,
–1,
![]() =
=![]()
![]()
![]()

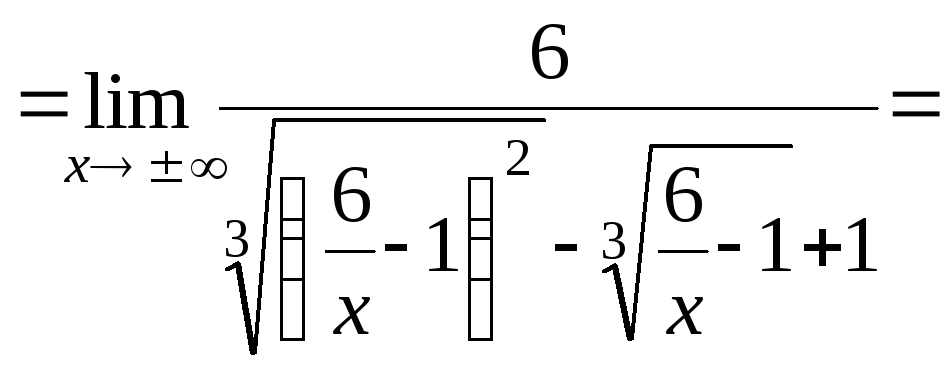
![]() 2.
2.
Следовательно,
![]() – наклонная асимптота (при х).
– наклонная асимптота (при х).
Монотонность и экстремумы.
![]()
![]()
![]()
![]() .
.
Необходимое условие экстремума:
![]()
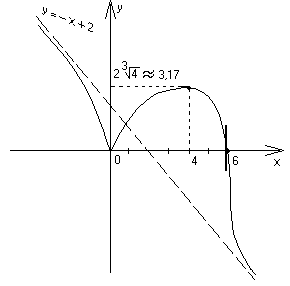
Получились три критические точки: х1 = 0, х2 = 4, х3 = 6, причем две из них х1 = 0 и х3 = 6 являются подозрительными на острый экстремум.
Достаточные условия монотонности и экстремумов:
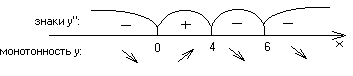
ymax=y(4)=
![]()
![]() 3,17
– гладкий максимум;
3,17
– гладкий максимум;
ymin=y(0)=
![]() 0
– острый минимум;.
0
– острый минимум;.
Выпуклость, вогнутость, точки перегиба:
![]()
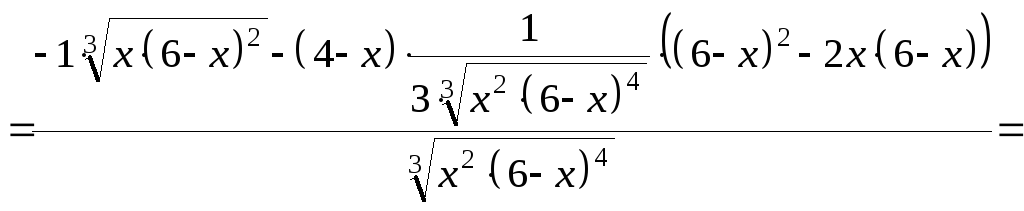

![]()
![]()
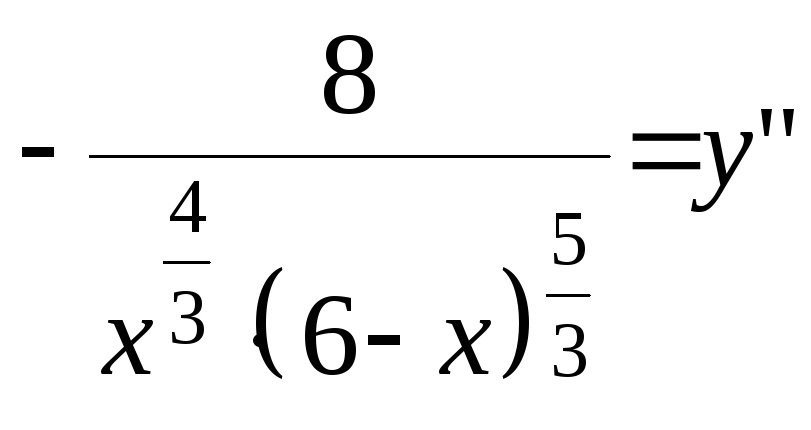 .
.
Необходимое условие для точек перегиба:
![]() Достаточные
условия:
Достаточные
условия:
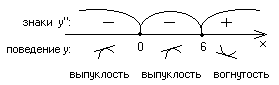
![]()
![]() в точке (6; 0) график функции имеет
перегиб.
в точке (6; 0) график функции имеет
перегиб.
Общая таблица свойств исследуемой функции:
|
x |
|
0 |
|
4 |
(4;6) |
6 |
(6;+) |
|
|
– |
не существует |
+ |
0 |
– |
0 |
– |
|
|
– |
не существует |
– |
– |
– |
не существует |
+ |
|
|
убывает, выпуклость |
острый min |
возрастает, выпуклость |
|
убывает, выпуклость |
точка перегиба |
убывает, вогнутость |
График функции:
Пример 4.
![]() .
.
Решение.
-
ООФ: х(0+).
2. Функция свойством четности не обладает, т.к. ее ООФ не является симметричной относительно нуля.
3. Функция непрерывна при х(0+), точек разрыва нет.
4. Асимптоты графика.
Возможна вертикальная асимптота на границе ООФ. Вычисляем
![]()
![]() –
–
прямая х = 0 является правосторонней вертикальной асимптотой графика.
Наклонная асимптота
(при х):
![]() ,
,
где
![]()
![]()
![]()
![]()
![]() 0,
0,
![]() =
=![]()
![]() =
=![]()
![]() 0.
0.
Следовательно,
![]() – горизонтальная асимптота (при х+).
– горизонтальная асимптота (при х+).
5. Монотонность и экстремумы.
![]()
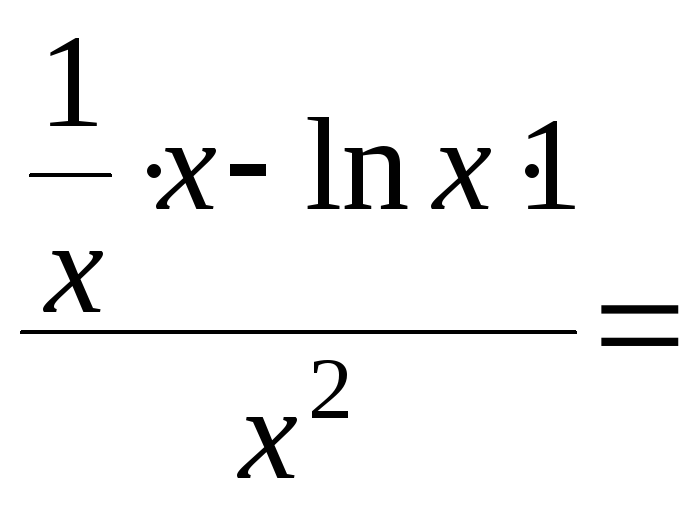
![]() – существует при хООФ.
– существует при хООФ.
Стационарная точка:
![]() (т.к.
(т.к.
![]() ).
).
Достаточное условие монотонности и экстремумов:
y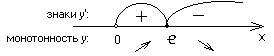 max
= y(
max
= y(![]() )
=
)
=
![]() 0,37.
0,37.
6. Выпуклость, вогнутость, точки перегиба:
![]()
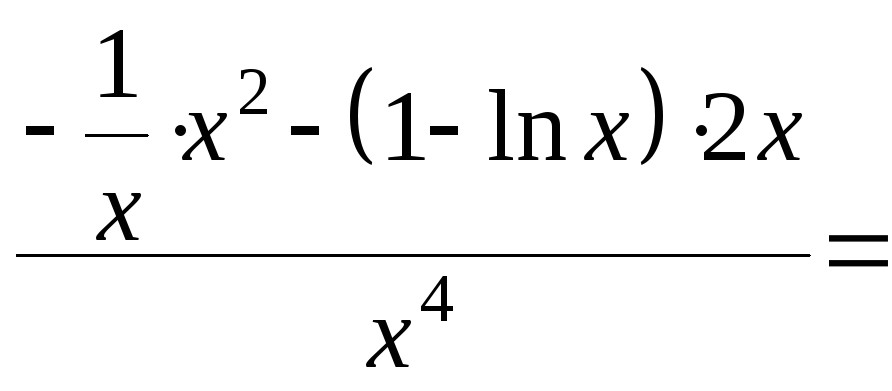
![]()
![]()
![]() – существует при хООФ.
– существует при хООФ.
![]() 0,
если –3+2
0,
если –3+2![]()
![]()
![]() – это подозрительная на перегиб точка.
– это подозрительная на перегиб точка.
Достаточные условия:
![]()

![]()
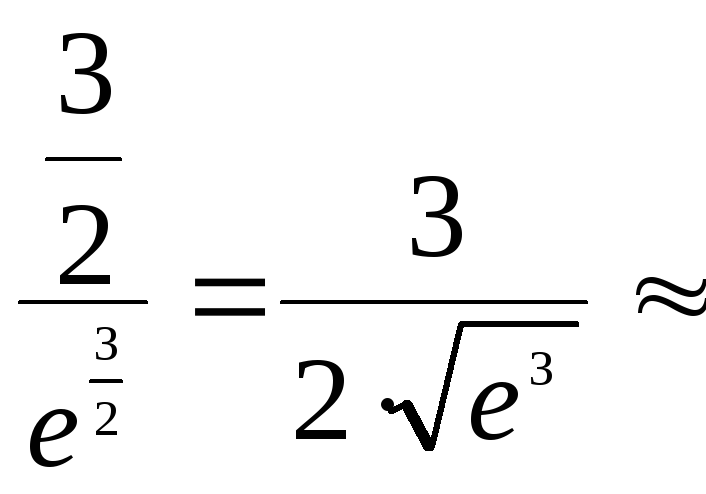 0,33.
0,33.
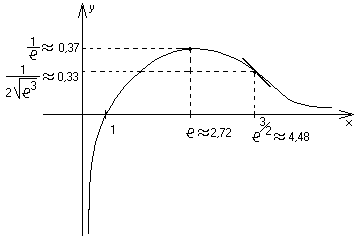
График функции
![]() :
:
Дополнительные упражнения.
Провести полное исследование функции и построить график.
|
1.
|
2.
|
|
3. |
4. |
|
5.
|
|
Ответы.
1. ООФ:
![]() ;
;
![]() ;
;
точка перегиба (0; 0).
2. ООФ:
![]() ;
асимптоты
;
асимптоты
![]() ;
;
![]() ;
;
![]()
точка перегиба (0; 0).
3. ООФ:
![]() ;
;
асимптота
![]() ;
;
![]() ;
;
![]() ;
;
точки перегиба имеют абсциссы

![]() ;
;
![]() .
.
4. ООФ:
![]() ;
асимптоты
;
асимптоты
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
5. ООФ:
![]() ;
;
асимптота
![]() ;
;
![]() ;
;
точки перегиба:
![]() и
и
![]() .
.
Список учебной литературы
-
Пискунов, Н.С. Дифференциальное и интегральное исчисления: Учеб.пособие для вузов: В 2-х т. Т.1/ Н.С. Пискунов. –М.: Интеграл-Пресс, 2001. - 416с.
-
Письменный, Д.Т. Конспект лекций по высшей математике: В 2-х ч. Ч.1/ Д.Т. Письменный. –М.: Рольф, 2001. - 288с.
-
Щипачев, В.С. Высшая математика/ В.С. Щипачев. –М.: Высш.шк., 1988. – 479с.
-
Берман, Г.Н. Сборник задач по курсу математического анализа/ Г.Н.Берман. –М.: Наука, 1985. – 416с.
-
Щипачев, В.С. Сборник задач по высшей математике/ В.С. Щипачев.
-М.: Высш.шк., 1998. – 304с.
-
Данко, П.Е. Высшая математика в упражнениях и задачах: В 2-х ч. Ч.1/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. –М.: Высш.шк., 1996. -304с.

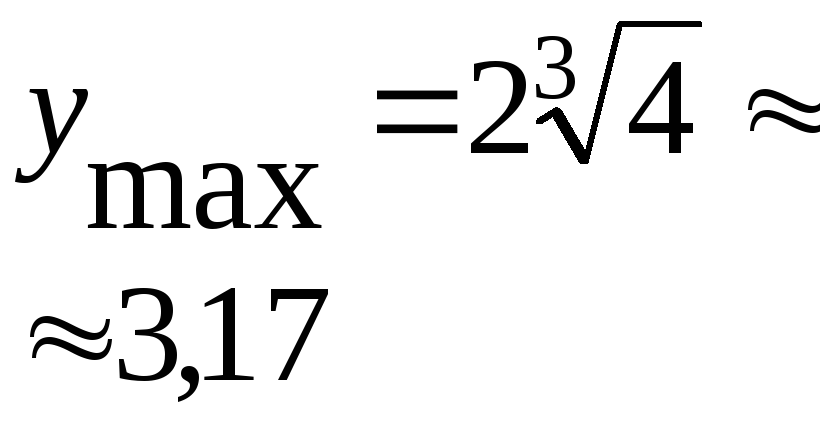 выпуклость
выпуклость