§3. Экстремумы функции.

Экстремумами функции называются ее максимумы и минимумы.

Точка х₀ называется точкой максимума функции , если существует такая двухсторонняя окрестность точки х₀ , что для всякой точки х  х₀ этой окрестности выполняется неравенство .

При этом число называется максимумом функции . Аналогично, если для всякой точки х  х₀ из некоторой окрестности точки х₀ выполняется неравенство , то х₀ называется точкой минимума, а число – минимумом функции .

Понятие экстремума связано с наличием окрестности точки х₀ из области определения функции. Поэтому функция может иметь экстремум лишь во внутренних точках области определения.

Необходимое условие экстремума.

Если непрерывная функция имеет экстремум в точке х₀, то ее производная в этой точке равна нулю или не существует.

Необходимое условие экстремум не является достаточным, т.е. точки, в которых или же не существует, не обязательно являются точками экстремумов функции.

Точки, в которых необходимое условие экстремумов выполняется, называются критическими, или подозрительными на экстремум.

Критические точки входят в область определения функции вместе с некоторой своей окрестностью, в которой функция является непрерывной и дифференцируемой (за исключением, быть может, самой критической точки, где может не существовать). Критические точки, в которых , называются еще стационарными, в них возможен только гладкий экстремум функции . Критические точки, в которых не существуют, являются подозрительными на острый экстремум функции . Наличие или отсутствие экстремума функции в ее критической точке проверяется чаще всего по следующим двум признакам:

Первый достаточный признак экстремума.

Если при переходе через критическую точку х₀ (слева направо) производная изменяет свой знак, то в точке х₀ есть экстремум причем, это максимум, если знак меняется с плюса на минус, и это минимум, если знак меняется с минуса на плюс. Если при переходе через критическую точку х₀ производная не изменяет свой знак, то в точке х₀ нет экстремума функции .

Второй достаточный признак экстремума.

Пусть х₀ – стационарная точка Первый достаточный признак экстремума функции , т.е. и существует вторая производная , непрерывная в точке х₀.

Если >0, то х₀ – точка минимума функции ;

если <0, то х₀ – точка максимума функции ;

если =0, то вопрос об экстремуме в точке х₀ остается открытым.

Пример 1.

Найти экстремумы функции .

Решение.

Находим .

Так как функция и ее производная определены и непрерывны при х(;+), то критическими точками являются только точки, в которых , т.е. х₁=0, х_2,3=2. Эти точки разбивают область определения функции на интервалы знакопостоянства ее производной (следовательно, на интервалы монотонности функции):

Н а основании первого достаточного признака экстремумов делаем вывод, что данная функция имеет три точки экстремумов:

x = –2 и х = 2 – точки минимумов, х = 0 – точка максимума.

В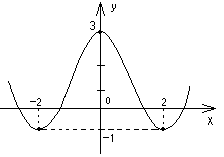ычисляя значение функции в точках экстремумов, находим экстремумы функции и строим схематически график:

y_min = y(–2) = –1;

y_max = y(0) = 3;

y_min = y(2) = –1;

В данной задаче все критические точки являются стационарными ,поэтому можно проверять в них и второе достаточное условие экстремумов. Для этого находим

Так как то х = –2 – точка минимума,

так как то х = 0 – точка максимума,

так как то х = 2 – точка минимума.

Ответ: ; ; .

Пример 2.

Найти экстремумы функции .

Решение.

Область определения функции х(–;+).

Вычисляем производную .

Находим точки, в которых выполняется необходимое условие экстремумов:

, если  х = –1;

не существует, елси  х = 0.

Получились две критические точки, причем, вторая из них (х = 0) является подозрительной на острый экстремум.

Проверяем достаточное условие монотонности функции и экстремумов (первое):

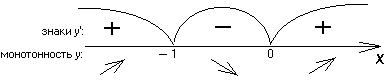
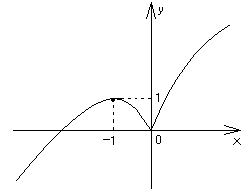
x = –1 – точка max;

х = 0 – точка min (острого);

;

.

Ответ: ; .

Пример 3.

Исследовать функцию на монотонность и экстремумы .

Решение.

Область определения функции: х  1.

Находим производную

Необходимое условие экстремумов:

  х₁ = 0, х₂ = 2 – это стационарные точки

не существует  (х–1)² = 0  х = 1 – не является критической точкой, так как не входит в область определения функции.

Достаточное условие монотонности и экстремумов:

– точка max, – точка min.

Вычисляем значения функции в точках экстремумов:

;

.

Строим схематический чертеж по результатам исследования:

Ответ:

возрастает при х(;0) и (2;+),

убывает при х(0;1) и (1;2).

Пример 4.

Найти экстремумы функции .

Решение.

Область определения функции: х > 0.

Находим производную .

Необходимое условие экстремумов:

   ;

не существует – таких х нет на области определения функции.

Таким образом, – единственная точка, подозрительная на экстремум. Проверим в ней второе достаточное условие экстремума:

=   – это точка min функции.

==.

Ответ: =.

Дополнительные упражнения.

1. ;	2. ;
3. ;	4. ;
5. ;	6. ;
7. ;	8. ;
9. ;	10. ;
11. ;	12. .

Ответы.

1. ;	2. ;
3. ;	4. ;
5. ;	6. ;
7. ;	8. Экстремумов нет;
9.	10. ;
11.	12. .