Метод линейной корреляции(метод Пирсона).

Статический анализ точности технологического процесса производиться после того, как станок проработал некоторое время, необходимое для стабилизации температуры технологической системы. Это время колеблется от 60 до 120 минут. В результате погрешности обработки, вызываемые температурными деформациями элементов системы превратятся из функциональных в постоянные. Статистический анализ посредством больших выборов заключается в следующем: со станка берётся текущая выборка, состоящая из деталей, приготовленных подряд, одна за другой, при неизменной настройке и других неизменных условиях.

Объём выборки устанавливается в зависимости от желаемой точности надёжности меры рассеивания σ, суммарной погрешности обработки. Для практического использования можно принять точность оценки σ по выбранному S(дисперсия), равную с вероятностью α=0,95. Тогда объём выборки достаточно сделать равной n=50. Все детали должны быть измерены шкальным измерительным инструментом с ценой деления шкалы равной (1/6…1/10)2δ, где 2δ – допуски на измеряемый размер.

На основании результатов измерений детали выборки составляется таблица распределения размеров выборки.

Таблица 1.

№		№		№		№		№
1	56	11	40	21	34	31	27	41	13
2	15	12	51	22	33	32	31	42	14
3	30	13	59	23	12	33	20	43	28
4	56	14	45	24	25	34	34	44	39
5	35	15	36	25	33	35	17	45	35
6	51	16	43	26	16	36	35	46	62
7	27	17	56	27	21	37	24	47	36
8	48	18	40	28	27	38	9	48	26
9	46	19	31	29	25	39	30	49	33
10	62	20	26	30	20	40	17	50	20

Далее производим группировку исходных данных. С этой целью определяем размах варьированных значений.

;

R- радиус значений;

- максимальное значение;

- минимальное значение;

мкм;

Размах разбивается на n интервалов группировки. Для партии из N=50…100 объектов исследования, число интервалов принимается равным от [6;9]. Примем n=6.

Ширина интервала принимается одинаковой, мкм. Тогда границы интервалов могут быть записаны:

………………..

Для компенсации погрешности измерения необходимо, чтобы величина была выше шкалы цены деления средства измерения, в котором проводилось измерение объекта. Для вычислений частот и частности значений случайной величины в интервале построим вспомогательную таблицу.

Таблица 2. Вычисление частот и частностей.

№ инт.	Интервал				Середина		Частота		Частность
	свыше			до(вкл)			усл. об.	циф. зн.
1	8			17	12,5			9	0,18
2	17			26	21,5			9	0,18
3	26			35	30,5			16	0,32
4	35			44	39,5			6	0,12
5	44			53	48,5			4	0,08
6	53			62	57,5			6	0,12

Σ

50

1

По данным табл.2 построим гистограмму распределения случайной величины отражающей дифференциальный закон распределения случайной величины. Масштаб гистограммы выбирают так, чтобы её высота относилась к основанию как 5/8.

Рис.1 Гистограмма.

8

26

35

44

53

17

62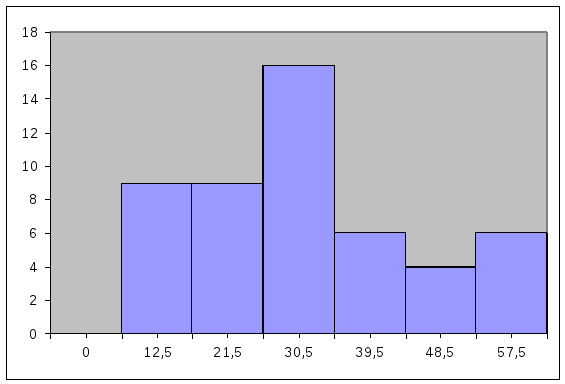

Строим полигон распределения случайной величины.

Рис.2. Полигон.

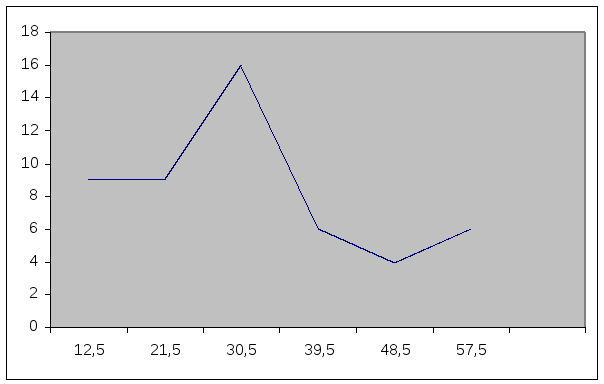
Полигоном распределения называют эмпирическое распределение случайной величины. Для вычисления параметров строим вспомогательную таблицу 3. Обозначим через середины интервалов, примем .

Таблица 3. Вычисление параметров эмпирического распределения.

№ инт.
1	12,5	9	-3	-27	81	-243	729
2	21,5	9	-2	-18	36	-72	144
3	30,5	16	-1	-16	16	-16	16
4	39,5	6	0	0	0	0	0
5	48,5	4	1	4	4	4	4
6	57,5	6	2	12	24	48	96
	Σ	50	-3	-45	161	-279	989

Вычисляем начальные моменты:

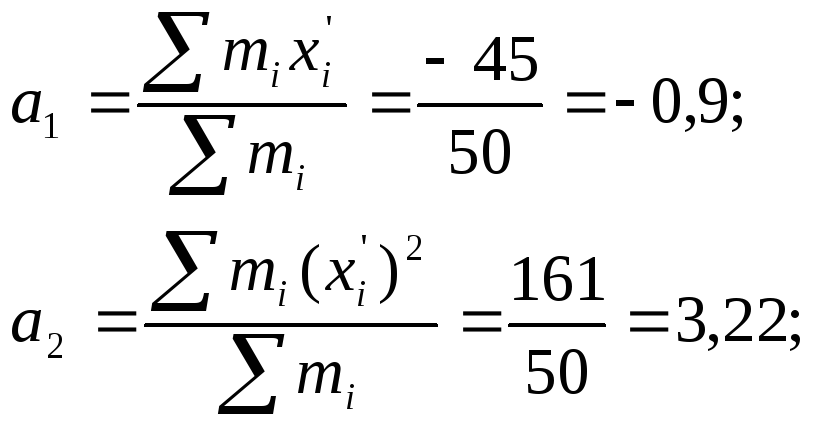
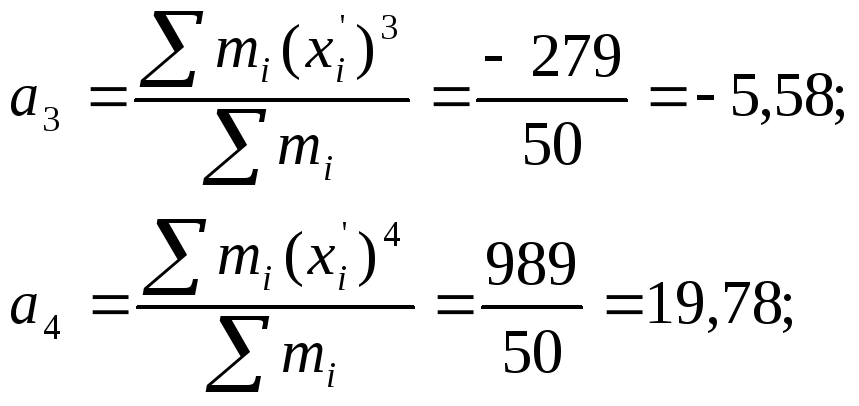
Вычисляем центральные моменты:

Вычисляем среднее значение и среднеквадратичное отклонение:

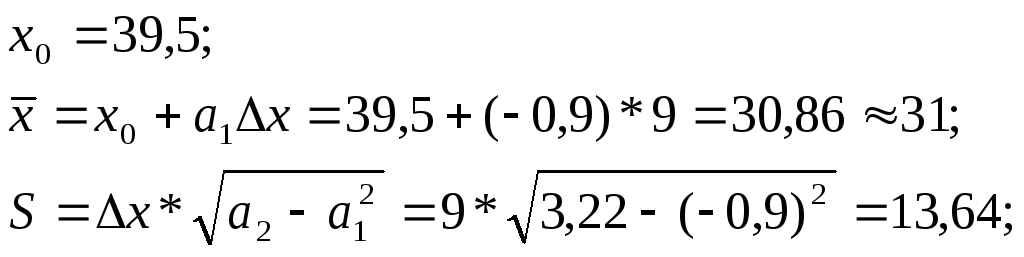
Вычисляем показатель асимметрии кривой распределения:

эмпирическая кривая сдвинута влево относительно кривой нормального кривой нормального распределения.

Вычисляем показатель крутизны(эксцесса):

эмпирическая кривая ниже кривой нормального распределения.

Построим графики эмпирической и выровненной кривой распределения. Вычисления произведём с помощью вспомогательной таблицы по нормальным законам распределения случайной величины.

Таблица 4. Вычисления параметров выровненной кривой распределения.

№ инт.	Середина
1	12,5	9	-18,5	-1,36	0,1582	0,1044	5,22
2	21,5	9	-9,5	-0,67	0,3187	0,2103	10,515
3	30,5	16	-0,5	-0,04	0,3986	0,2630	13,15
4	39,5	6	8,5	0,62	0,3292	0,2172	10,86
5	48,5	4	17,5	1,28	0,1758	0,1160	5,8
6	57,5	6	26,5	1,94	0,0608	0,0401	2,005
-	-	-	-	-	-	Σ	47,55

По данным таблицы 4 строим выровненную и эмпирическую кривые распределения.

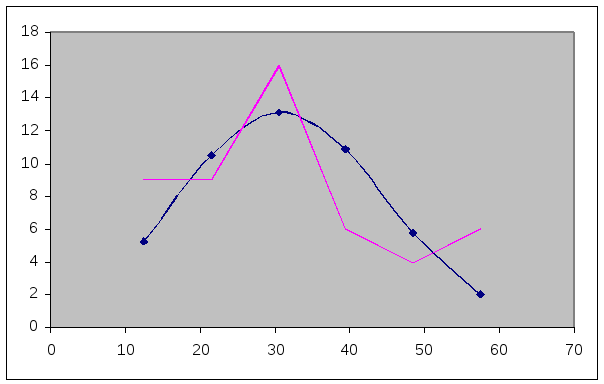
Проверим правильность выдвинутой гипотезы в виде закона распределения случайной величины с помощью критерия согласия Пирсена . При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом(нормальным законом распределения в данном случае) принимается сумма квадратов отклонений частностей от теоретической вероятности от теоретической вероятности попадания отдельного результата измерений в j-ый интервал, причём каждое слагаемое принимается с весовым коэффициентом.

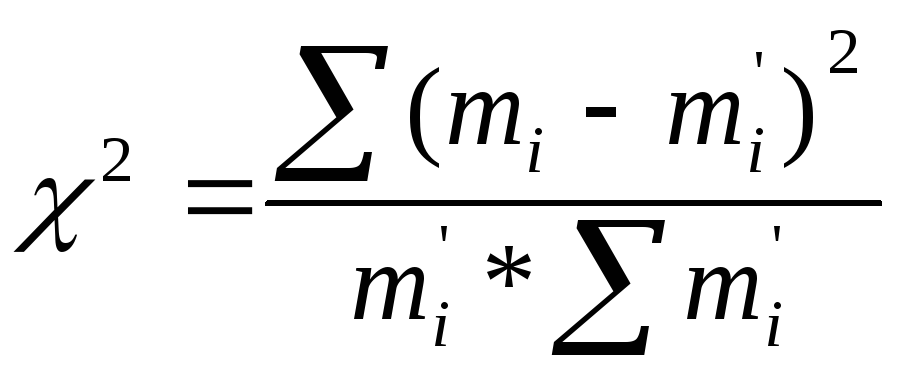
Выполним вычисления с помощью специальной таблицы. Если в некоторые интервалы попадает менее 5 значений, то они объединяются с соседними.

Таблица 5. Вычисления коэффициента согласия Пирсена .

№ инт.
1	9		5,22		3,78	14,288	2,737
2	9		10,515		-1,515	2,295	0,2183
3	16		13,15		2,85	8,123	0,6177
4	6		10,86		-4,86	23,620	2,175
5	4	10	5,8	7,805	2,195	4,818	0,617
6	6		2,005
-	-		-		-	Σ	6,365

Определяем :

После нахождения следует определить число степеней свободы:

,

где n – число сравниваемых частот(объединённые частоты на концах принимаются за одну частоту);

r – число параметров теоретической функции распределения(нормальный закон распределения двухпараметрический).

По таблице определяем:

Так как , то кривые согласуются и принятый закон соответствует нормальному.