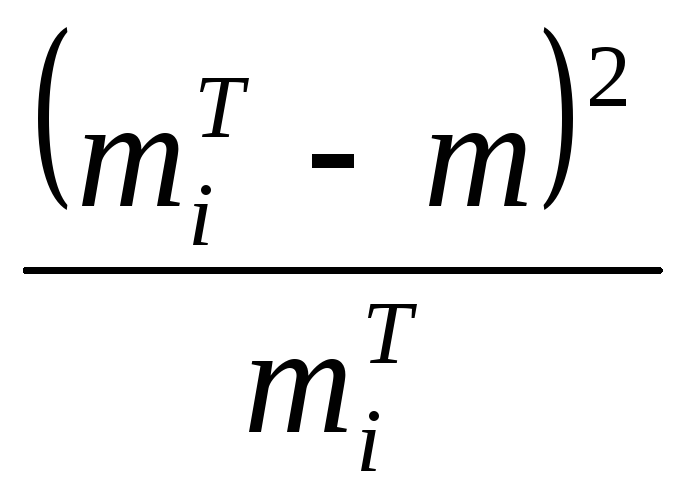9. Вибірковий метод
Def. 9.1 Генеральною сукупністю називається множина усіх об’єктів, що містить ознаку, яка досліджується. Кількість елементів Г.С. називається її обсягом.
Суцільне дослідження генеральної сукупності не завжди можливе або бажане. У таких випадках з генеральної сукупності відбирають деяку кількість об’єктів, досліджують їх та переносять встановлені отримані дані на генеральну сукупність.
Def. 9.2 Вибірковою сукупністю (вибіркою) називається підмножина генеральної сукупності, яку відбирають для дослідження. Кількість елементів вибірки називається її обсягом.
Головна вимога до В – вона повинна бути репрезентативною, тобто за змістом і структурою відображати Г.С.
Приклади.
Існує два принципово різних метода відбору: випадковий та невипадковий. До останніх відносяться: типічний, механічний, серійний та їх комбінації.
Випадковий відбір може реалізовуватися у двох варіантах: відібраний об’єкт повертається або не повертається у Г.С.
Приклади.
Відповідно, вибірки називаються «власно-випадкова повторна» та «власно-випадкова безповторна». У подальшому: повторна та безповторна.
Як буде показано далі, безповторна краща.
Оцінка параметрів Г.С.
Точкова оцінка
Нехай постає задача дослідити
кількісну ознаку у Г.С. Припустимо, що
з теоретичних міркувань нам відомо, за
яким законом ця ознака розподілена.
(нормальний, показників, рівномірний,
тощо). Кожний з них визначається деякою
кількістю параметрів (нормальній та
рівномірний – двома, показниковий –
одним) Нехай треба оцінити значення
деякого параметра
у Г.С.
Для цього робиться
різних вибірок, у яких шуканий параметр
приймає значення
.
Оскільки вибірки випадкові, то і обчислені
значення є випадковими, їх можна вважати
значеннями ВВ
.
Саме ця ВВ і називається оцінкою параметра
у Г.С. Наприклад, середнє вибіркове
може розглядатися як оцінка
.Така
оцінка називається точковою.
Вимоги до точкової оцінки: незсуненість, ефективність та слушність (несмещеная, еффективная, состоятельная).
Def. 9.3 Оцінка
називається незсуненною, якщо
.
Зауваження :ВВ та число.
Def. 9.4 Оцінка
називається ефективною, якщо вона має
найменшу дисперсію порівняно з будь-якою
іншою оцінкою, яка будується на вибірках
такого ж обсягу.
Def. 9.5 Оцінка
називається слушною, якщо при нескінченному
зростанні кількості вибірок (
),
вона за імовірністю збігається до
.
Детально розглядати не будемо, зауважимо лише те, що вибіркова середня (8.1) (8.2).є незсуненою оцінкою середньої генеральної, а вибіркова дисперсія (8.3) (8.4) є зсунотою оцінкою генеральної дисперсії.
Інтервальна оцінка
Більш вживаною є інтервальна оцінка. Вона встановлює інтервал, якому з певною імовірністю належить параметр, що оцінюється.
,
де
-
границі інтервалу,
- довірчий інтервал,
- довірча імовірність, або надійність
оцінки.
Ми будемо використовувати інтервальні оцінки лише двох параметрів: середнього значення кількісної ознаки та долі (частки) якісної ознаки у Г.С., спираючись на відповідні показники у вибірці. Тому довірчі інтервали будуть симетричними відносно показників вибірки:
де .
.-.гранична
помилка.
З урахуванням властивостей модуля можна записати:
для першого співвідношення
-
для другого -
для третього -
При цьому для кількісної ознаки використовують Теорему Чебишева з уточнення Ляпунова, а для якісної – Бернуллі, такох з уточненням Ляпунова.
Для вибіркового метода ці теореми набувають вигляду:
(9.1)
,
де (9.2)
,
- середньоквадратична похибка вибірки.
Ця величина є точковою оцінкою дисперсії
Г.С., яка, як зазначалося раніше, є зсуненою
і залежить від типу вибірки (повторна
чи безповторна), обсягу Г.С. -
обсягу вибірки -
.
Обчислюється так:
при оцінці середньої (кількісна ознака)
вибірка повторна:
(9.3)
вибірка безповторна:
(9.4)
при оцінці долі (якісна ознака)
вибірка повторна:
(9.5)
вибірка безповторна:
(9.6)
Якщо нам невідомо, то добуток
замінюється верхнєю межею: 0.25.
Таким чином дані формули
містять три незалежні параметри:
.
Задаючи дві з них, ми можемо обчислити
третю, що визначає три типи задач
вибіркового метода.
Як встановити повторна чи ні.
Приклади. 1. При автоматичному виготовленні пиріжків з капустою з метою встановлення іх якості зроблена вібірка обсягом 100 пиріжків. Якісними серед них виявилося 79. В якому проміжку з ймовірністю 0,95 слід очикувати долю якісних виробів в партії у 10000 пирожків?
2. Середня вага становить 127 г., а дисперсія ваги – 140. Яка ймовірність того, що в усій партії середня вага пирожків лежатиме в діапазоні 125-129 г.
3 За технологією ймовірність виготовлення якісного пиріжка 0,9. Скільки треба з’їсти пиріжків, щоб з йомовірністю 0,95 можна було стверджувати, що в усій партії доля якіснтх виробів належила проміжку 0,85-0,95.
1.
2.
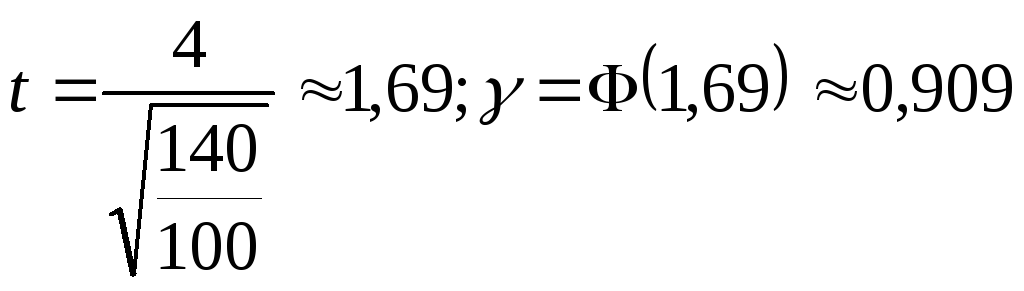
3.
10. Порівняння теоретичного та емпіричного законів розподілу.
Критерій Пірсона
Результати спостереження деякого параметра системи (не тільки економічної) можуть бути представлені у вигляді варіаційного ряду (дискретного або інтервального). При подальшому дослідженні, наприклад при прогнозуванні) працювати з таблицею незручно, потрібно мати аналітичний опис поведінки. Зокрема, якщо параметр, що досліджується знаходиться під впливом багатьох чинників, его можна вважати випадковою величиною. Тоді нам необхідні аналітично виражені закони розподілу ВВ: диференціальний, якщо ВВ можна вважати неперервною та інтегральний, у випадку будь-якої ВВ.
Постає задача визначити за яким з теоретичних законів розподілен даний параметр, або близько до якого.
Def. 10.1 Закон, що визначається варіаційним рядом називається емпіричним.
Def. 10.2 Гіпотезою називається будь-яке твердження стосовно емпіричного закону.
Наприклад: математичне сподівання дорівнює 7, дисперсія дорівнює 34, закон розподілу нормальний и таке інше. Оскільки вони стосуються статистичних характеристик та перевіряються статистичними методами, то називається статистичними. Розрізняються прості та складені гіпотези.
Приклади.
Нехай висловлена гіпотеза
.
Поряд з гіпотезою, яку ми перевіряємо,
формулюється так звана конкуруюча
(альтернативні) гіпотеза. Її позначають
.
Приклади.
Гіпотеза відносно закону розподілу є, зрозуміло, складеною. Гіпотезу можна прийняти або відхилити.
У процесі перевірки гіпотези можливі 4 ситуації:
Правильна гіпотеза прийнята; Хибна гіпотеза відхилена;
Правильна гіпотеза відхилена; Хибна гіпотеза прийнята.
Останні два випадки є помилками.
Якщо правильна гіпотеза відхилена, то таку помилку називається помилкою першого роду.
Якщо хибну гіпотезу приймають, то таку помилку називається помилкою другого роду.
Наслідки помилок.
Для перевірки
використовують спеціально відібрану
випадкову величину, закон розподілу
якої відомо. Фішер, Стьюдент, Пірсон .
Статистичним критерієм (у
подальшому просто критерієм) називається
ВВ яку використовують для перевірки
.
Позначимо її
.
Спектр цієї ВВ розбивається на дві
множини: одна з них містить значення
критерію, при яких
приймається, а інша – при яких відхиляється.
Def. 10.3 Критичною областю називається множина значень критерію, при яких гіпотеза відхиляється.
Розрізняють двосторонні та односторонні (лівосторонні, правосторонні) критичні області.
Монотонність критерію.
Побудова правосторонньої критичної області.
Задається достатньо маленьке
число
.Вважаючи,
що гіпотеза
виконується, знаходять
із співвідношення:
.
(10.1)
Величина
називається рівнем значимості. Виходячи
з (10.1),
– це імовірність помилки першого роду.
На основі варіаційного ряду
обчислюється
.
Якщо
,
то гіпотеза відкидається. Якщо ж
,
то нема підстав відкидати
,
гіпотеза приймається. Прийняття гіпотези
ще не означає її доведення, потрібні
додаткові дослідження. В той же час
відхилення гіпотези є категоричним.
При побудові таблиць. Частота у інтервалі повинна бути більше 5. Якщо ні, то інтервали об’єднуються. Теоретичні частоти обчислюються як добуток теоретичної імовірності влучення у інтервал на обсяг вибірки.
Для нормального закону:
,
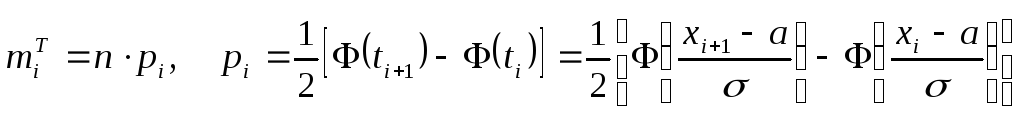а для показникового:
Після таблиці – чому
.
Нехай кількість інтервалів
.
Тоді ВВ, які утворюють
також
,
але вони не є незалежними, оскільки ми
їх вже використовували при обчисленні
параметрів, тобто наклали зв’язки
«связи». Так, для гіпотези про нормальній
закон розподілу, це були -
,
три, для гіпотези показникового закону
– дві:
.
Отже кількість степенів свободи,
,
буде: для нормального закону
,
а для показникового -
.
Варіант №1
1. Початковий інтервальний варіаційний ряд:
|
|
0 - 11 |
11 - 22 |
22 - 33 |
33 - 44 |
44 - 55 |
55 - 66 |
66 - 77 |
77 - 88 |
88 - 99 |
|
|
2 |
5 |
12 |
14 |
7 |
9 |
4 |
1 |
1 |
2. Гістограма:
3. Обчислення числових параметрів емпіричного закону розподілу:
|
|
|
|
|
|
|
|
|
Табл. 1 |
|
|
||
|
|
0 - 11 |
11 - 22 |
22 - 33 |
33 - 44 |
44 - 55 |
55 - 66 |
66 - 77 |
77 - 88 |
88 - 99 |
Сума |
||
|
|
2 |
5 |
12 |
14 |
7 |
9 |
4 |
1 |
1 |
55 |
||
|
|
5,50 |
16,50 |
27,50 |
38,50 |
49,50 |
60,50 |
71,50 |
82,50 |
93,50 |
445,50 |
||
|
|
11,00 |
82,50 |
330,00 |
539,00 |
346,50 |
544,50 |
286,00 |
82,50 |
93,50 |
2315,50 |
||
|
|
60,5 |
1361,25 |
9075 |
20751,5 |
17151,75 |
32942,25 |
20449 |
6806,25 |
8742,25 |
117339,75 |
||
|
|
-98055,8 |
-83886 |
-37346 |
-653,18 |
2836,568 |
56065,54 |
101648,7 |
65939,264 |
135796,744 |
142346,16 |
||
|
|
3588842 |
2147484 |
545246 |
2351,46 |
20990,6 |
1031606 |
2988473 |
2663946,27 |
6979952,64 |
19968891,54 |
||
|
|
|
|
42,1 |
|
|
361,04 |
|
19,00 |
|
|
||
|
|
|
|
|
|
|
0,377268 |
|
-0,21 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
=
=
=
=
=
Вигляд гістограми, значення
та
дозволяють висунути гіпотезу що
емпіричний закон розподілу близький
до нормального.
Перевірку цієї гіпотези
проведемо за допомогою критерію Пірсона.
Для цього порівняємо емпіричний закон
з теоретичним, який має такі характеристики:
.
Табл.. 2
|
|
|
|
|
|
|
|
|
|
|
|
|
(-∞; 22) |
-∞ |
22 |
-∞ |
-1,06 |
-1 |
-0,7109 |
0,1446 |
7,9503 |
7 |
0,1136 |
|
(22; 33) |
22 |
33 |
-1,06 |
-0,48 |
-0,7109 |
-0,3688 |
0,1711 |
9,4078 |
12 |
0,7143 |
|
(33; 44) |
33 |
44 |
-0,48 |
0,10 |
-0,3688 |
0,0797 |
0,2243 |
12,3338 |
14 |
0,2251 |
|
(44; 55) |
44 |
55 |
0,10 |
0,68 |
0,0797 |
0,5035 |
0,2119 |
11,6545 |
7 |
1,8589 |
|
(55; 66) |
55 |
66 |
0,68 |
1,26 |
0,5035 |
0,7923 |
0,1444 |
7,9420 |
9 |
0,1409 |
|
(66; +∞) |
66 |
∞ |
1,26 |
∞ |
0,7923 |
1 |
0,1039 |
5,7118 |
6 |
0,0145 |
|
Сума |
|
|
|
|
|
|
1,0000 |
55,0000 |
|
3,0673 |
Таким чином,
.
Кількість степенів свободи:
.
Критичні
точки розподілу
(рівень значимості,
).
|
Число
степенів свободи,
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
7,8 |
9,5 |
11,1 |
12,6 |
14,1 |
15,5 |
16,9 |
18,3 |
.
Оскільки
,
то гіпотеза приймається.
Варіант №2
1. Початковий інтервальний варіаційний ряд:
|
|
0 - 11 |
11 - 22 |
22 - 33 |
33 - 44 |
44 - 55 |
55 - 66 |
66 - 77 |
77 - 88 |
88 - 99 |
|
|
22 |
18 |
12 |
11 |
7 |
9 |
4 |
1 |
1 |
2. Гістограма:
Обчислимо параметри емпіричного закону розподілу:
|
|
|
|
|
|
|
|
|
Табл. 3 |
|
|
|
|
0 - 11 |
11 - 22 |
22 - 33 |
33 - 44 |
44 - 55 |
55 - 66 |
66 - 77 |
77 - 88 |
88 - 99 |
Сума |
|
|
22 |
18 |
12 |
11 |
7 |
9 |
4 |
1 |
1 |
85 |
|
|
5,50 |
16,50 |
27,50 |
38,50 |
49,50 |
60,50 |
71,50 |
82,50 |
93,50 |
445,50 |
|
|
121,00 |
297,00 |
330,00 |
423,50 |
346,50 |
544,50 |
286,00 |
82,50 |
93,50 |
2524,50 |
|
|
665,5 |
4900,5 |
9075 |
16304,75 |
17151,75 |
32942,25 |
20449 |
6806,25 |
8742,25 |
117037,3 |
|
|
|
|
|
|
|
|
|
|
|
|
Вигляд гістограми та близькість
значень
дозволяє висунути гіпотезу що емпіричний
закон розподілу близький до показникового.
Перевірку цієї гіпотези
проведемо за допомогою критерію Пірсона.
Для цього порівняємо емпіричний закон
з теоретичним. Єдиний параметр, яким
визначається цей закон,
,
знайдемо як середнє значення:
,
звідки
.
|
|
|
|
|
|
|
|
|
|
|
|
|
(0; 11) |
0 |
11 |
0 |
-0,43 |
1,0000 |
0,6489 |
0,3511 |
29,8413 |
22 |
2,0604 |
|
(11; 22) |
11 |
22 |
-0,43 |
-0,86 |
0,6489 |
0,4211 |
0,2278 |
19,3648 |
18 |
0,0962 |
|
(22; 33) |
22 |
33 |
-0,86 |
-1,30 |
0,4211 |
0,2733 |
0,1478 |
12,5663 |
12 |
0,0255 |
|
(33; 44) |
33 |
44 |
-1,30 |
-1,73 |
0,2733 |
0,1773 |
0,0959 |
8,1546 |
11 |
0,9928 |
|
(44; 55) |
44 |
55 |
-1,73 |
-2,16 |
0,1773 |
0,1151 |
0,0623 |
5,2917 |
7 |
0,5515 |
|
(55; 66) |
55 |
66 |
-2,16 |
-2,59 |
0,1151 |
0,0747 |
0,0404 |
3,4339 |
9 |
9,0220 |
|
(66; ∞) |
66 |
∞ |
-2,59 |
- ∞ |
0,0747 |
0,0000 |
0,0747 |
6,3473 |
6 |
0,0190 |
|
Сума |
|
|
|
|
|
|
1,0000 |
85,0000 |
85 |
12,7675 |
Таким чином,
.
Кількість степенів свободи:
.
.
кільки
,
то гіпотеза відхиляється.