7. Закон великих чисел
Теорема 7.1. Нерівність Маркова.
Якщо
ВВ, спектр якої – множина невід’ємних
чисел та вона має скінчене математичне
сподівання, то для будь-якого доданого
виконується нерівність:
(7.1)
Доведення. Твердження теореми виконується як для ДВВ, так і для НВВ. Проведемо його для НВВ.
За означенням
,
а оскільки ВВ приймає лише невід’ємних
значень, то, по перше
,
по друге
.
Нехай
,
тоді
Оскільки
,
то
і за властивістю визначеного інтегралу:
.
Остаточно,
.
Враховуючи, що
,
маємо:
(7.2)
Події
протилежні, отже
.
Крім того, у НВВ
,
тому
.
З урахуванням (7.2), отримаємо (7.1).
Теорема 7.2. Нерівність Чебишева.
Якщо ВВ
має скінчені математичне сподівання
та дисперсію, для будь-якого
виконується нерівність:
(7.3)
Доведення. Нерівність
еквівалентна нерівності
,
отже:
.
Розглянемо ВВ
.
Вона приймає лише невід’ємних значень
і, враховуючи, що
,
то до неї можна застосувати нерівність
Маркова.
.
Оскільки за означенням,
,
то отримаємо твердження теореми (7.3).
Частинні випадки нерівності Чебишева.
1. Стосовно частоти при НПВ:
,
отже:
(7.4.)
Приклади.
2. Стосовно частості
:
,
отже:
(7.5)
Def. 7.1. Послідовність ВВ
називається збіжною за імовірністю до
величини
,
якщо для будь-якого
.
Позначається це:
.
Теорема 7.3. Теорема Бернуллі.
При НПВ частість за імовірністю збігається до імовірності:
(7.6)
Доведення. Переходячи у (7.5) до границь, отримаємо
,
але враховуючи, що
,
отримаємо (7.6).
Теорема 7.4. Теорема Чебишева.
Якщо
попарно незалежні ВВ, дисперсії яких
обмежені, то при
середнє арифметичне ВВ збігається за
імовірністю до середнього арифметичного
їх математичних сподівань.
Доведення. Нехай
.
Розглянемо ВВ
.
Її числові характеристики:
Підставляючи ці значення у нерівність Чебишева (7.3), отримаємо:
.
Переходячи до границь, отримаємо:
,
але,
,
отже:
.
Ця рівність і визначає збіжність за
імовірністю.
Уточнення Ляпунова:
Теорема Чебишева:
(7.7)
Теорема Бернуллі:
(7.8)
Елементи математичної статистики
8. Статистичні сукупності та їх характеристики
Def. 8.1. Статистичною сукупністю називається множина однорідних об’єктів, які містять однакову ознаку, що досліджується. Приклади.
Ознака, що досліджується може бути кількісною або якісною.
У більшості випадків, якісна ознака є альтернативною, тобто деяка характеристика може бути у об’єкту дослідження або ні. Приклади.
Тоді можна ввести числову характеристику, яка прийме значення 1, якщо об’єкт містить дану якість і 0, якщо не містить.
Розглянемо сукупність, у якій
досліджується кількісна ознака
.
Позначимо кількість об’єктів
.
Розглянемо випадок, коли кількісна
ознака може приймати окремі значення,
тобто є дискретною.
Def. 8.2. Варіантами називається значення кількісної ознаки, які спостерігалися у сукупності.
Будемо позначати їх
.
Зауваження:
.
Def. 8.3. Частотою варіанти
називається кількість об’єктів
статистичної сукупності, у яких
спостерігалось це значення ознаки.
Позначимо її
.
Зрозуміло, що
.
Def. 8.4. Частістю (відносною
частотою) називається відношення частоти
варіанти до загальної кількості елементів
сукупності. Позначимо її
.
Def. 8.5. Дискретним варіаційним рядом називається відображення варіант на відповідні частоти або частості. Як правило, варіанти записуються у перший рядок в порядку зростання, а відповідні частоти (частості) – у другому. Такий ряд називається ранжируваним.
|
|
-1 |
2 |
3 |
5 |
7 |
10 |
11 |
15 |
|
|
5 |
8 |
14 |
16 |
10 |
14 |
18 |
15 |
|
|
0,05 |
0,08 |
0,14 |
0,16 |
0,1 |
0,14 |
0,18 |
0,15 |
Якщо кількісна ознака може
приймати будь-яке значення із деякої
множини, тобто є неперервною, то будується
інтервальний варіаційний ряд. Довжини
інтервалів позначимо
.
|
|
1 - 4 |
4 -8 |
8 - 14 |
14 - 16 |
16 - 22 |
22 - 25 |
|
|
2 |
7 |
12 |
14 |
11 |
4 |
На практиці інтервальний варіаційний ряд замінюють дискретним варіаційним рядом, приймаючі в якості варіант середини відповідних інтервалів.
|
|
2,5 |
6,0 |
11,0 |
15,0 |
19,0 |
23,5 |
|
|
2 |
7 |
12 |
14 |
11 |
4 |
|
|
0,04 |
0,14 |
0,24 |
0,28 |
0,22 |
0,08 |
Def. 8.6. Полігоном варіаційного ряду називається множина точок координатної площини абсцисами яких є варіанти, а ординатами відповідні частоти або частості частоти або частості. Приклади.
Def. 8.7. Гістограмою інтервального
варіаційного ряду називається фігура
на координатній площині, яка складається
з відрізків, що паралельні вісі абсцис,
довжини яких дорівнюють інтервалам
ряду і розташованими на відстані
від вісі абсцис. Приклади.
|
|
1 - 4 |
4 -8 |
8 - 14 |
14 - 16 |
16 - 22 |
22 - 25 |
|
|
2 |
7 |
12 |
26 |
11 |
4 |
|
|
0,67 |
1,75 |
2,0 |
13,0 |
1,83 |
1.33 |
Def. 8.8. Варіаційним розмахом
називається різниця між найбільшою та
найменшою варіантами:
.
Застосовується і для дискретних і для
інтервальних варіаційних рядів. У
нашому прикладі:
Def. 8.9. Модою дискретного
варіаційного ряду називається варіанта,
якій відповідає найбільша частота.
Позначається
.
У нашому прикладі:
Def. 8.10. Медіаною дискретного
варіаційного ряду називається варіанта,
яка є серединою ранжируваного ряду,
тобто сума частот менших варіант дорівнює
сумі частот більших варіант. Позначається
.
У нашому прикладі:
(приблизно).
Існує декілька числових
характеристик варіаційного ряду, які
називається середніми (арифметичне,
геометричне, гармонічне, тощо). За нашими
позначеннями, середнє арифметичне.
дорівнює:
.
Якщо усі варіанти додатні,
то середнє геометричне дорівнює:
.
Середнє значення дискретного варіаційного ряду обчислюється за формулами:
,
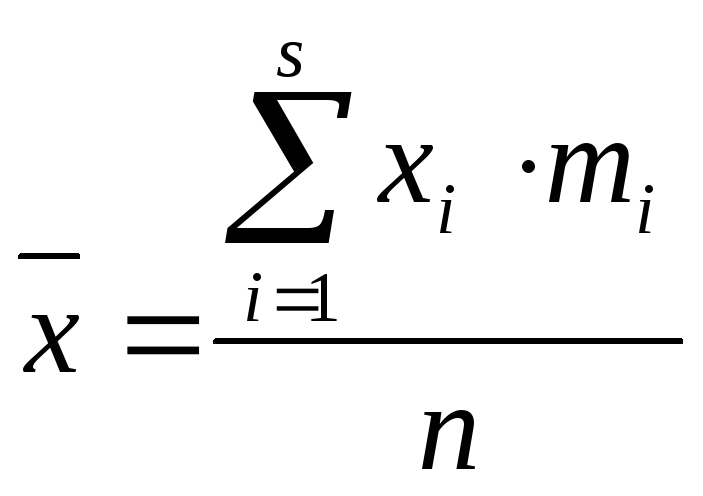(8.1)
або:
.
(8.2)
Ці значення називається середніми зваженими, причому ваговими коефіцієнтами є частоти або частості.
Якщо кожна варіанта
зустрічається один раз (
),
то (8.1) набуває виду:
,
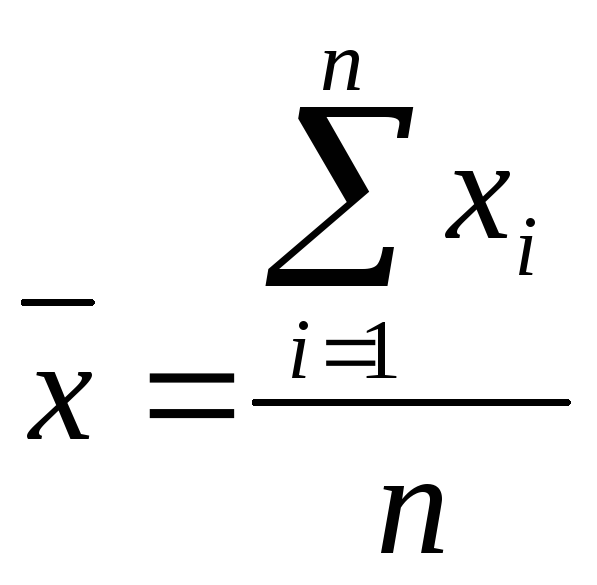тобто співпадає з середнім арифметичним.
Дисперсія дискретного варіаційного ряду обчислюється за формулою:
,
(8.3)
або:
,
(8.4)
Відповідно, середнє квадратичне
відхилення:
.
|
|
-1 |
2 |
3 |
5 |
7 |
10 |
11 |
15 |
сума |
|
|
5 |
8 |
14 |
16 |
10 |
14 |
18 |
15 |
100 |
|
|
0,05 |
0,08 |
0,14 |
0,16 |
0,1 |
0,14 |
0,18 |
0,15 |
1,00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,05 |
0,16 |
0,42 |
0,8 |
0,7 |
1,4 |
1,98 |
2,25 |
7,66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3,74978 |
2,562848 |
3,040184 |
1,132096 |
0,04356 |
0,766584 |
2,008008 |
8,08134 |
21,3844 |
|
|
|
|
|
|
|
|
|
|
|
Як бачимо, ці показники співпадають з відповідними для ДВВ якщо розглядати частість в якості імовірності, а середнє зважене – як математичне сподівання.
Розглянемо ще декілька числових характеристик, однакових як для дискретних варіаційних рядів, так і для ДВВ.
Def. 8.11. Коефіцієнтом варіації називається відношення середнього квадратичного відхилення до середнього значення:
(8.5)
Def. 8.12. Початковим моментом
-ого
порядку ВВ
називається математичне сподівання ВВ
:
Зокрема
.
Def. 8.13. Центральним моментом
-ого
порядку порядку ВВ
називається
математичне сподівання ВВ
:
Зокрема
.
Ці моменти використовуються для побудови комплексних характеристик ВВ. Зокрема, коефіцієнтів асиметрії та ексцесу.
(8.6)
(8.7)
У нормальному розподілу:
.
Для варіаційних рядів початкові та центральні моменти обчислюються за формулами:
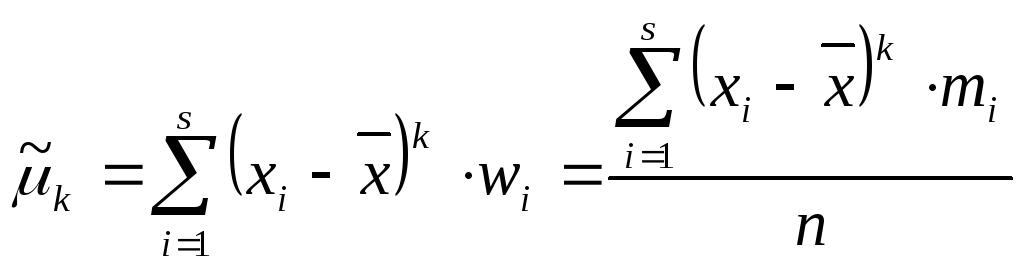(8.8)
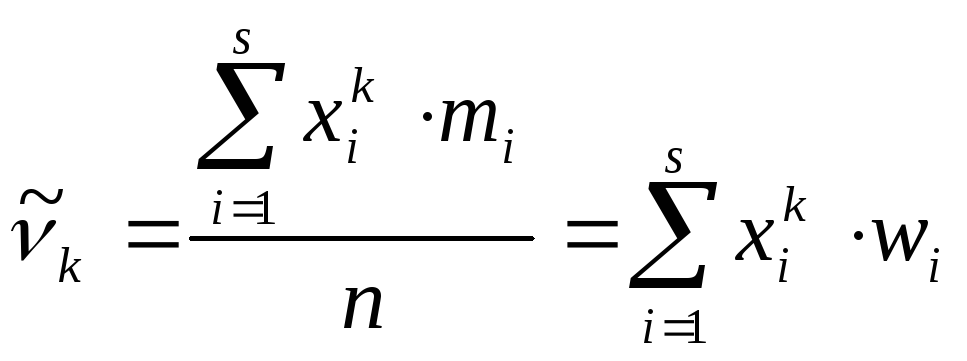(8.9)
Ексцес та асиметрія позначаються
