6.3.Аппроксимация характеристик нелинейных элементов

Для того чтобы была возможность аналитически рассчитывать цепи с нелинейными элементами, необходимо иметь математические выражения для характеристик элементов. Сами эти характеристики обычно являются экспериментальными, т.е. полученными в результате измерений соответствующих элементов, а затем приводятся как справочные (типовые) данные. Процедуру математического описания некоторой заданной функции в математике называют аппроксимацией этой функции. Существует целый ряд типов аппроксимации: по выбранным точкам, по Тейлору, по Чебышеву и др. В конечном итоге необходимо получить математическое уравнение, которое с какими-то заданными требованиями удовлетворяло исходной, аппроксимирующей функции. Для этого применяют полиномы: степенные, экспоненциальные и тригонометрические.

Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.

Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точек на заданной функции и составляется система уравнений:

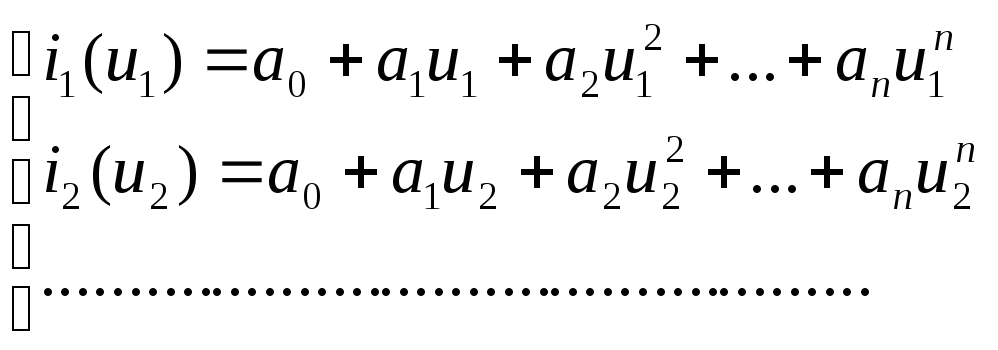
Из этой системы находятся коэффициенты а₀, а₁, а₂, …, а_n.

В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома).

Можно использовать экспоненциальный полином:

Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одно точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные.

Аппроксимация по Батерворту: выбирается простейший полином:

В этом случае можно определить максимальное отклонение ε.

Аппроксимация по Чебышеву является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной.

Чебышев установил, что должно выполняться:

В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий.

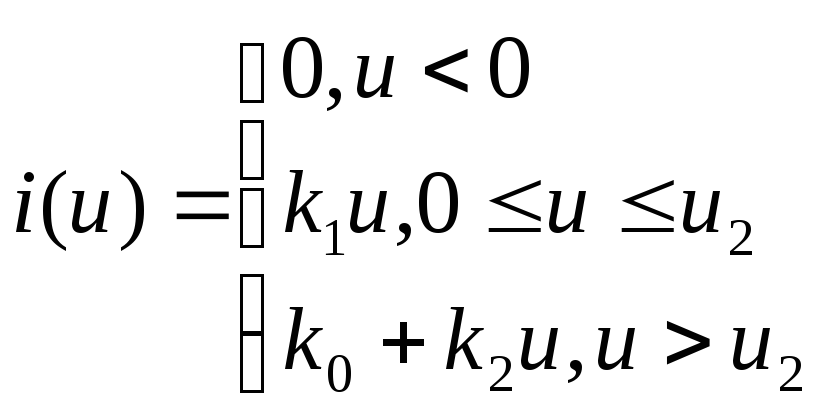
6.4. Определение реакции нелинейного элемента на гармоническое воздействие

1. Гармоническое воздействие малой амплитуды, постоянная составляющая

, где - постоянная составляющая, - амплитуда малой величины.

В этом случае можно отдельно рассмотреть реакцию на постоянную составляющую и на гармоническое воздействие.

Здесь можно использовать понятие статического и дифференциальных сопротивлений, а также графический метод.

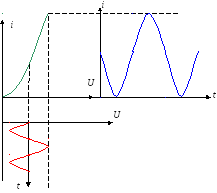
, где ,

2. Большая амплитуда напряжения

Используется графический метод (строить реакцию путем переноса точек).

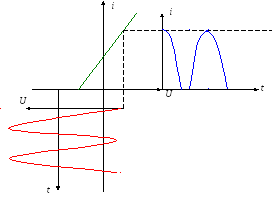
6.5. Анализ спектра реакции в нелинейном элементе

Рассмотрим на примере спектра тока при подаче гармонического напряжения. Если элемент линейный, то мы получаем гармонический ток (одна составляющая). Если элемент нелинейный, то получим много составляющих.

Для определения спектра, необходимо найти амплитуды спектральных составляющих и фазы.

Частоты всех составляющих будут кратны основной частоте или частоте воздействия. Самый простой способ – применить степенную аппроксимацию.

Затем необходимо воспользоваться формулами разложения:

Число составляющих гармоник зависит от степени полинома, при этом четные степени дают четные гармоники, нечетные – нечетные.

Начальные фазы все нулевые.

Таким образом, можно приблизительно определить спектр. Можно определить спектры при других аппроксимациях, но это более сложно математически.

Например:

Также применяют метод нескольких ординат. В частности рассмотрим метод трех ординат.

Составляют систему уравнений:

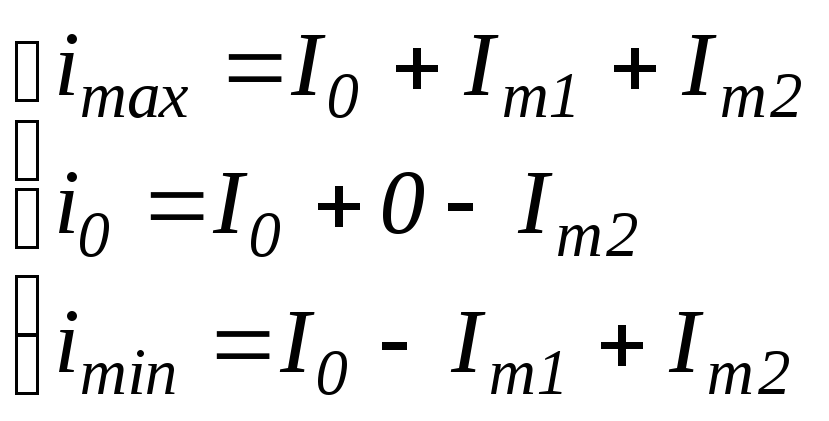, из которой находят амплитуды гармоник.

Можно использовать большее количество точек (метод пяти, семи и т.д. ординат).