
- •Операторный метод анализа линейных систем. Введение. Основные понятия теории управления.
- •Операторный метод анализа линейных систем.
- •Описание элементов системы.
- •Уравнения элементов.
- •Передаточная функция.
- •Весовые и переходные функции звена.
- •Характеристики типовых звеньев.
- •Описания систем.
- •Структура и структурная схема системы.
- •Соотношения «вход - выход».
- •2. Структурные представления.
- •Устойчивость.
- •Устойчивость звена по входу.
- •Алгебраические критерии устойчивости.
- •Устойчивость по начальным условиям.
- •4. Устойчивость системы.
- •Установившаяся реакция и частотная характеристика.
- •Определение реакции при гармоническом воздействии.
- •Анализ типовых структур.
- •Соединения с отрицательной обратной связью.
- •Обобщенный критерий Найквиста.
4. Устойчивость системы.
Система осуществляет устойчивые преобразования от каждого внешнего входа к каждому внешнему входу. Следовательно, устойчивость системы обеспечивается, если
-
строго реализуемы все соотв. Переходные функции;
-
характеристический многочлен
 - устойчив.
- устойчив.
По
аналогии, следует считать систему
устойчивой, если при любых начальных
условиях и отсутствии внешних воздействий
процессы
 на всех выходах -> 0 при t->
на всех выходах -> 0 при t-> .
Однако тогда для всех выходов справедливы
однородные уравнения
.
Однако тогда для всех выходов справедливы
однородные уравнения

И следовательно система устойчива по начальным условиям, если устойчив ее характеристический многочлен.
-
и 2) достаточны для устойчивости системы в обоих смыслах.
-
Установившаяся реакция и частотная характеристика.
-
Определение реакции при гармоническом воздействии.
Определение:
назовем
установившейся реакцией на заданное
воздействие
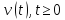 ,
такую функцию
,
такую функцию
 ,
что
,
что

Где
 - решение (1.2) при нулевых начальных
условиях.
- решение (1.2) при нулевых начальных
условиях.
Пусть
воздействие
 .
.
Теорема
4.1.
если звено H(p)
является устойчивым, то устойчивая
реакция на гармоническое воздействие
(4.2) является той же тригонометрической
функцией с той же частотой
 и амплитудой
и амплитудой
 и относительным сдвигом фазы
и относительным сдвигом фазы

Доказательство:
Найдем
реакцию на


Согласно (1.6)

Т.к. звено устойчиво, то выполнено условие теоремы 3.1

Следовательно :

-
по определению
 -
преобразования
-
преобразования
Следовательно:

 -
является
установившейся реакцией на
-
является
установившейся реакцией на
 .
.


В
силу линейности реакция на сумму равна
сумме реакций и отсюда вытекает, что
реакцией на
 является
является
 ,
а реакцией на
,
а реакцией на
 является
является
 .
.
Пример:


Рассмотрим:

Применим критерий Рауса.
|
k |
0 |
1 |
2 |
|
|
1 |
1 |
1 |
|
|
1 |
1 |
1 |
|
|
2 |
1 |
1 |
|
|
1 |
1 |
1 |
|
|
|
1 |
1 |
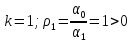 ;
;
 :
вычисляем
:
вычисляем
 ;
;
 :
:
 .
.
 ;
;
 :
вычисляем
:
вычисляем
 ;
;
 – многочлен
устойчив.
– многочлен
устойчив.
Тогда

 .
.
 .
.
 .
.

Где

Комплекснозначная
функция
 называется комплексной частичной
характеристикой.
называется комплексной частичной
характеристикой.
Если
изменять
 от 0 до
от 0 до
 ,то
каждое
,то
каждое
 определяется точкой на комплексной
плоскости для каждого
определяется точкой на комплексной
плоскости для каждого
 ,
то такое множество точек называется
годографом частотной характеристики.
,
то такое множество точек называется
годографом частотной характеристики.
Всякое комплексное число можно представить 2-мя вещественными числами следующими способами:
-
Модулем и аргументом

-
Вещественной и комплексной частью
 .
.
Если
 – АЧХ,
– АЧХ,
 – ФЧХ,
– ФЧХ,
 – вещественная ЧХ,
– вещественная ЧХ,
 - мнимая ЧХ.
- мнимая ЧХ.
Если
известны
 и
и
 ,
то, согласно теореме 4.1, для определения
амплитуды и фазы устойчивой реакции на
гармоническое воздействие можно
пользоваться следующим приемом, используя
результаты теоремы 1.4.1.
,
то, согласно теореме 4.1, для определения
амплитуды и фазы устойчивой реакции на
гармоническое воздействие можно
пользоваться следующим приемом, используя
результаты теоремы 1.4.1.
Устойчивая реакция на полиномиальное воздействие. Рассмотрим внешнее воздействие:

Теорема 4.2 Устойчивая реакция устойчивого звена на полиномиальное воздействие (4.3) также является многочленом, представимым виде:

где:

Доказательство:

Разложим
 в ряд Тейлора в точке t.
Т.к. v(t)-многочлен
N-ой
степени, то в этом разложении следует
оставить только (N+1)
первых членов; тогда:
в ряд Тейлора в точке t.
Т.к. v(t)-многочлен
N-ой
степени, то в этом разложении следует
оставить только (N+1)
первых членов; тогда:

Следовательно:


Существование предела

следует
из того факта, что h(t)
соответствует устойчивой по входу H(p),
имеет в своем представлении слагаемые
с
 ,
где
,
где
 .
Тогда сразу
.
Тогда сразу

С другой стороны:


Теорема доказана.
Следствия из теоремы 4.2.
-
Если
 .
То
.
То
 .
. -
Если
 то
то
 .
.
Пример:
Пусть
 ,
а
,
а
 .
Тогда
.
Тогда



и
 .
.
Эти результаты получены при изучении реакции одного звена.





