
- •Операторный метод анализа линейных систем. Введение. Основные понятия теории управления.
- •Операторный метод анализа линейных систем.
- •Описание элементов системы.
- •Уравнения элементов.
- •Передаточная функция.
- •Весовые и переходные функции звена.
- •Характеристики типовых звеньев.
- •Описания систем.
- •Структура и структурная схема системы.
- •Соотношения «вход - выход».
- •2. Структурные представления.
- •Устойчивость.
- •Устойчивость звена по входу.
- •Алгебраические критерии устойчивости.
- •Устойчивость по начальным условиям.
- •4. Устойчивость системы.
- •Установившаяся реакция и частотная характеристика.
- •Определение реакции при гармоническом воздействии.
- •Анализ типовых структур.
- •Соединения с отрицательной обратной связью.
- •Обобщенный критерий Найквиста.
2. Структурные представления.
В первой части §1.2 рассматривалась задача сведения звеньевой системы к системе, состоящей из одного входа и нескольких выходов.
Рассмотрим обратную задачу. Пусть существует одно некое сложное звено:

Где
 и
и
 – произв. многочлены степени
– произв. многочлены степени
 и
и
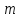 соответственно;
соответственно;
 и
и
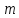 -
степени многочленов.
-
степени многочленов.
Как эту систему из 1-го звена преобразовать к эквивалентной системе, состоящей только из простых типовых звеньев. Имеет мест следующая:
Теорема:
Если
выполнено условие
 , то звено (2.15) эквивалентно системе,
состоящей только из звеньев типа
идеальных усилителей и интеграторов и
имеющей внешний вход
, то звено (2.15) эквивалентно системе,
состоящей только из звеньев типа
идеальных усилителей и интеграторов и
имеющей внешний вход
 и внешний выход
и внешний выход
 .
.
Схема доказательства:

При
 ,
,

 .
.
 составим
систему
составим
систему

Если
 -
решения этой системы, то всегда можно
подобрать такие
-
решения этой системы, то всегда можно
подобрать такие
 ,
что y
– решение исходного уравнения. Чтобы
это показать, выражаем все
,
что y
– решение исходного уравнения. Чтобы
это показать, выражаем все
 через
через
 и
и
 и подставляем в последнее уравнение
системы. Тогда перенося все члены с
и подставляем в последнее уравнение
системы. Тогда перенося все члены с
 влево, а с
влево, а с
 -вправо, приходим к следующему выводу:
-вправо, приходим к следующему выводу:
-
В левой части – такое же выражение, как и в части уравнения;
-
Приравнивая правые части, покажем, что однозначно определены такие
 ,
что при их выборе и правые части
совпадают.
,
что при их выборе и правые части
совпадают.
Но тогда, если ввести:
 ,
то
все 1-е (
,
то
все 1-е ( уравнение системы записывается
уравнение системы записывается
 -
это интеграторы, а последнее -ое уравнение
записывается
-
это интеграторы, а последнее -ое уравнение
записывается

Это
стандартное представление уравнения
связи, как и
 - что и доказывает теорему.
- что и доказывает теорему.
-
Устойчивость.
-
Устойчивость звена по входу.
Определение:
звено
называется
устойчивым по входу если
при любом входном воздействии
 и нулевых начальных условиях входная
реакция
и нулевых начальных условиях входная
реакция
 является ограниченной при любых
является ограниченной при любых
 и при
и при
 .
В противном случае звено неустойчиво.
.
В противном случае звено неустойчиво.
Теорема 1.3: (необходимое и достаточное условие устойчивости по входу).
Если звено описывается уравнением:
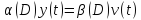 (3.1),
то по его устойчивости по входу необходимо
и достаточно (Н и Д) выполнение условия:
(3.1),
то по его устойчивости по входу необходимо
и достаточно (Н и Д) выполнение условия:

(Напоминаем,
что
 ,
а
,
а
 интеграл от 0 до
интеграл от 0 до
 от модуля весовой
функции звена ограничен.)
от модуля весовой
функции звена ограничен.)
Доказательство (Д): По определению весовой функции:

Пусть
 - ограниченная функция, тогда:
- ограниченная функция, тогда:

Но
тогда устойчивость
 следует из условия (3.2). (Мы доказали что
из
следует из условия (3.2). (Мы доказали что
из
 - ограничена и (3.2) следует
- ограничена и (3.2) следует
 – ограничен).
– ограничен).
Доказательство
(Н):
для доказательства необходимости
докажем, что существует такая ограниченная
функция
 ,
что если (3.2) – нарушается, то
,
что если (3.2) – нарушается, то
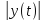 может быть сколь угодно большим, т.е.
может быть сколь угодно большим, т.е.
 - неограничен.
- неограничен.
Пусть
 :
:

 .
.
Тогда:

Следовательно,
если (3.2) нарушается,
 может оказаться больше любого заданного
числа. Значит (3.2) необходимо для
устойчивости. Теорема доказана.
может оказаться больше любого заданного
числа. Значит (3.2) необходимо для
устойчивости. Теорема доказана.
Применимость теоремы (3.1) связана с вычислением весовой функции звена.
Теорема 3.2 (2-ое Н и Д условие):
Для
выполнения условия (3.2) Н и Д чтобы
передаточная функция
 была ограничена по модулю при любых p,
с
была ограничена по модулю при любых p,
с
 .
.
Доказательство
(Д):
Пусть
 ограничена при
ограничена при
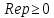 и положим
и положим
 ,
,
 корни многочлена
корни многочлена
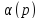 -
все различные (простые полюсы). Тогда,
т.к.
-
все различные (простые полюсы). Тогда,
т.к.
 - дробно-рациональная функция, то:
- дробно-рациональная функция, то:

 ;
;
 -
многочлен
степени
(m-n).
-
многочлен
степени
(m-n).
Из
предположения ограниченности
 при
при
 следует:
следует:
-
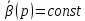 ,
т.е.
,
т.е.

-
 (иначе
при
(иначе
при
 существуют корни в правой полуплоскости,
существуют корни в правой полуплоскости, а это приводит к тому, что
а это приводит к тому, что
 ограничено при
ограничено при
 ).
).
Но
тогда
 и можно найти весовую функцию
и можно найти весовую функцию
 для передаточной функции
для передаточной функции


и тогда

Но тогда

(используем
тот факт, что

Доказательство (Н): необходимость вытекает из определения весовой функции


Тогда:

Необходимость
доказана. (для
 ).
).
Теперь можно, как следствия доказанных теорем 3.1 и 3.2 сформулировать:
Критерий устойчивости по входу.
Устойчивость по входу имеет место, если выполняются 2 условия:
-
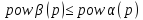 -
что соответствует условию строгой
реализации (называется условием строгой
реализуемости) ;
-
что соответствует условию строгой
реализации (называется условием строгой
реализуемости) ; -
 имеет
корни только с отрицательными
вещественными частями ( называется
условием устойчивости характеристического
многочлена).
имеет
корни только с отрицательными
вещественными частями ( называется
условием устойчивости характеристического
многочлена).
