
- •Операторный метод анализа линейных систем. Введение. Основные понятия теории управления.
- •Операторный метод анализа линейных систем.
- •Описание элементов системы.
- •Уравнения элементов.
- •Передаточная функция.
- •Весовые и переходные функции звена.
- •Характеристики типовых звеньев.
- •Описания систем.
- •Структура и структурная схема системы.
- •Соотношения «вход - выход».
- •2. Структурные представления.
- •Устойчивость.
- •Устойчивость звена по входу.
- •Алгебраические критерии устойчивости.
- •Устойчивость по начальным условиям.
- •4. Устойчивость системы.
- •Установившаяся реакция и частотная характеристика.
- •Определение реакции при гармоническом воздействии.
- •Анализ типовых структур.
- •Соединения с отрицательной обратной связью.
- •Обобщенный критерий Найквиста.
-
Алгебраические критерии устойчивости.
В математике известны эффективные методы проверки устойчивости многочленов. Начнем с необходимого условия.
Теорема 3.3 (критерий Стодолы).
Если
многочлен
 с
с
 устойчив, то все его коэффициенты
устойчив, то все его коэффициенты
 .
.
Доказательство:
Пусть
у
 существуют вещественные корни
существуют вещественные корни
 и пары комплексно сопряженных корней
и пары комплексно сопряженных корней
 .
Тогда в разделении
.
Тогда в разделении
 по корням будут присутствовать двучлены
по корням будут присутствовать двучлены
 и трехчлены
и трехчлены
 .
.
 .
Т.к.
.
Т.к.
 – устойчивый многочлен, то
– устойчивый многочлен, то
 .
Но тогда все коэффициенты в
.
Но тогда все коэффициенты в
 -
положительны, а следовательно, порождаемые
ими ( по обобщенной теореме Виета)
коэффициенты многочлена
-
положительны, а следовательно, порождаемые
ими ( по обобщенной теореме Виета)
коэффициенты многочлена
 ,
являются суммой их произведений
,
являются суммой их произведений
 .
Теорема доказана.
.
Теорема доказана.
Критерий
Стодолы - дост. Для n=1
и
n=2.
В остальных случаях его можно использовать
как критерий неустойчивости:
(Если А-> B,
то
 ).
).
Если среди коэффициентов многочлена есть неположительные, то такой многочлен неустойчив.
Для
определения устойчивости многочлена
( без вычисления его корней) лучше всего
использовать алгоритм
Рауса.
Пусть заданы
 ,
,
 ,
коэффициент многочлена
,
коэффициент многочлена

Тогда если k – номер шага алгоритма, то:
-
k =1: вычисляем
 .
Если
.
Если
 ,
то многочлен неустойчив.
,
то многочлен неустойчив. -
Если
 ,
то k
= k+1
и, начиная с
,
то k
= k+1
и, начиная с
 вычисляем:
вычисляем:

(Если
 ).
).
-
Если все
 ,
то многочлен устойчив.
,
то многочлен устойчив.
Для
 и
и
 - этот алгоритм легко выполняется в
общем виде и полученные в этих случаях
условия называются условием
Рауса.
- этот алгоритм легко выполняется в
общем виде и полученные в этих случаях
условия называются условием
Рауса.
Рассмотрим пример использования этого алгоритма:
|
|
0 |
1 |
2 |
3 |
|
|
|
2 |
2 |
2 |
2 |
|
|
|
6 |
6 |
6 |
6 |
|
|
|
10 |
7 |
7 |
7 |
|
|
|
9 |
9 |
5 |
5 |
|
|
|
5 |
14/3 |
14/3 |
49/15 |
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
1/3 |
6/7 |
7/5 |
75/49 |
 ;
;
 :
вычисляем
:
вычисляем
 ;
;
 :
:
 ;
;
 :
:
 ;
;
Заполняем 1 столбец.
 ;
;
 :
вычисляем
:
вычисляем
 ;
;
 :
:
 ;
;
 ;
;
 :
вычисляем
:
вычисляем
 ;
;
 :
:
 ;
;
 $
$
 – многочлен
устойчив.
– многочлен
устойчив.
Вывод:
многочлен с
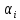 =
устойчив.
=
устойчив.
Существуют условия Рауса - Гурвица на коэффициенты многочлена в общем виде, но практически удобнее пользоваться данным критерием.
-
Устойчивость по начальным условиям.
Начиная с §1, было сделано предположение, что дифференциальные соотношения (1.1) будут рассматриваться при нулевых начальных условиях.
Если начальные условия – не нулевые, то решение можно записать как суммы двух решений:
-
 -
как решение однородного уравнения:
-
как решение однородного уравнения:


Где
 – константа, если
– константа, если
 - простой корень;
- простой корень;
и
многочлены, степени на 1 ниже, чем
кратность корня
 .
.
-
 -
частное решение неоднородного уравнения
-
частное решение неоднородного уравнения

В
качестве
 выберем решение с неявными начальными
условиями:
выберем решение с неявными начальными
условиями:


Тогда:

Наличие ненулевых начальных условий приводит к появлению фактора, изменяющего характер связи между входом и выходом.
Определение:
звено
называется устойчивым по начальным
условиям, если вызываемый ими эффект
( )
исчезает при
)
исчезает при
 .
.
Тогда, из определения и (3.3) вытекает, что существует критерий устойчивости по начальным данным:
Система
устойчива по начальным условиям, если
все корни характеристического множества
имеют
 .(
т.е.
.(
т.е.
 является устойчивым многочленом).
является устойчивым многочленом).
Т.к.
устойчивость по начальным данным
совпадает с одним из условий устойчивости
по входу, то при выполнении этих условий
употребляется более краткий термин –
устойчивое
звено.
А соответственно переходную
 называют устойчивой
переходной функцией.
называют устойчивой
переходной функцией.








