Теорема о вычетах курсовая (2)

Содержание

Введение

1. Теоретическая часть

1.1. Определение вычета функции.

1.2. Основная теорема о вычетах.

1.3. Вычисление вычета относительно полюса.

1.4. Вычет функции относительно бесконечности.

2. Практическая часть.

2.1. Интеграл от 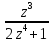по контуру .

2.2. Интеграл от по контуру .

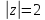2.3. Интеграл от 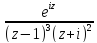по контуру .

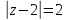Заключение

Список литературы

Введение

В комплексном анализе вычетом заданного объекта называется объект, характеризующий локальные свойства объекта заданного. Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения.

Для возможности более полного изучения свойств функции вводится понятие вычета в бесконечности, при этом она рассматривается как функция на сфере Римана.

В большинстве случаев теория вычетов применяется для вычисления разного рода интегральных выражений с помощью основной теоремы о вычетах. Теорема о вычетах является мощным инструментом для вычисления интеграла функции по замкнутому контуру.

1. Теоретическая часть

1.1. Определение вычета функции.

Вычетом аналитической функции f относительно её изолированной особой точки z=f ϵ C называется коэффициент с_-1 при первой отрицательной степени разложения функции f в ряд Лорана в окрестности этой точки.

Вычет обозначают:

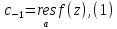
Пусть дана функция 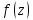голоморфная в некоторой точке a, тогда по теореме Коши имеем:

где контур С – гладкий замкнутый, при чем 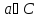и малый настолько, что функция 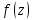остается голоморфной всюду внутри контура, включая точки самого контура. Значение интеграла 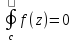по такому контуру равно нулю. Если же a будет изолированной особой точкой функции 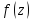и замкнутый контур C целиком лежит в окрестности этой точки а, то значение интеграла будет отличным от нуля. Это значение, как следует из теоремы Коши, не зависит от формы контура С и может быть вычислено. В окрестности точки a (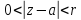) функция 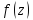может быть разложена в ряд Лорана

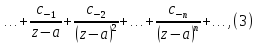
который будет равномерно сходящимся на линии С, так как контур С лежит в окрестности точки а. Интегрируя почленно ряд вдоль линии С, получим:

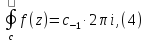
так как имеют место равенство

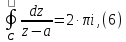
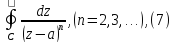
Значение интеграла назовем вычетом функции 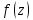относительно точки а.

Определение. Вычетом функци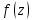и относительно её изолированной особой точки 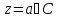называется коэффициент при первой отрицательной степени разложения функции 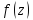в ряд Лорана в окрестности этой точки.

Обозначение вычета:

В итоге имеем:

1.2. Формулировка теоремы о вычетах.

Сформулируем основную теорему о вычетах. Пусть 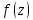есть функция голоморфная во всякой точке области G, кроме конечного числа особых точек а₁,а₂,…,а_k. Обозначим через Γ кусочно-гладкий замкнутый контур, содержащий в себе точки а₁,а₂,…,а_k и целиком лежащий в области G. При этих условиях 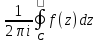равен сумме вычетов функции относительно точек а₁,а₂,…,а_k. Это утверждение представляет собой основную теорему о вычетах.

Она широко используется для вычисления интегралов. Для этого необходимо определить вычеты всех особых точек а₁,а₂,…,а_k, лежащих внутри контра Γ. Поэтому важно дать более простой способ вычисления вычетов, не требующий разложения в ряд Лорана в каждом отдельном случае. Такой способ известен для случая, когда особая точка является полюсом.

1.3. Вычисление вычета относительно полюса.

Пусть точка a является простым полюсом функции 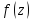. В этом случае главная часть разложения Лорана содержит лишь одну первую отрицательную степень :

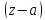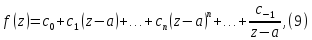
Умножая обе части разложения на 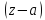, получаем:

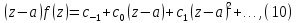
Так как правая часть последнего равенства есть обыкновенный степенной ряд, то его сумма будет непрерывной функцией в точке a. Следовательно, переходя в последнем равенстве к пределу при z стремящемся к a получим:

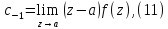
Эта формула позволяет быстро определить вычет функции относительно простого полюса. Её можно обобщить на случай произвольного полюса n-го порядка. В этом случае разложение Лорана будет:

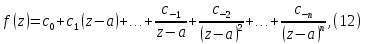
Умножим обе части этого уравнения на 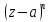, получим:

Продифференцировав последнее равенство (n-1) раз, мы получим в правой части обыкновенный степенной ряд, свободный член которого будет:

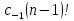. Следовательно, имеем:

Откуда находим:

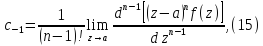
Получаем формулу для вычисления вычета функции относительно полюса а порядка n.

В частности при n=1:

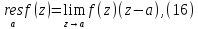
На практике оказывается полезной небольшая модификация последней формулы.

Пусть функция f(z) в окрестности простого полюса z=a имеет вид

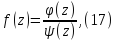
Где φ и ψ – аналитические в точке z=a функции, причем φ(a)≠0, ψ(a)=0, ψ’(a)≠0. Подставив в формулу (16) имеем:

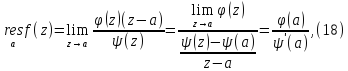
1.4. Вычет функции относительно бесконечности.

Вычетом функции относительно бесконечности называется коэффициент при первой отрицательной степени разложения функции f в окрестности бесконечности, умноженный на -1.

Вычет функции относительно бесконечности определяется коэффициентом правильной чести ряда Лорана и поэтому может быть отличным от нуля и в том случае, когда бесконечность является устранимой особой точкой функции f(z) .

Пусть бесконечность является устранимой особой точкой функции f. Введем обозначение 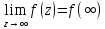. Тогда:

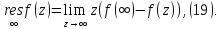
Так же следует упомянуть теорему(т. 1):

Если f(z) есть функция, голоморфная во всякой точке расширенной плоскости комплексного переменного z, кроме конечного числа особых точек, то сумма вычетов всех её особенностей всегда равна нулю.

2. Практическая часть.

2.1. Интеграл от 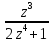по контуру .

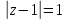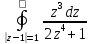
Для вычисления данного интеграла изобразим область, по которой ведется интегрирование.

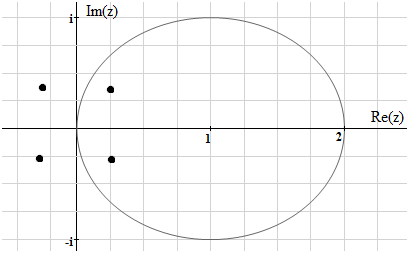
Найдем особые точки, определим вид особенности и выяснить попадают ли эти точки в область интегрирования.

Для того, чтобы найти особые точки приравняем знаменатель нулю:

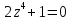
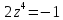
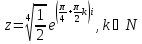
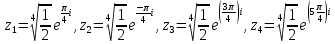– особые точки типа простой полюс. Две из них(z₁, z₂) попадают в область, по которой производится интегрирование. Следовательно, можем применить теорему о вычетах следующим образом:

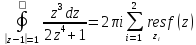
Применив формулу (18) получим:

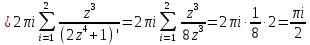
2.2. Интеграл от 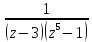по контуру .

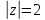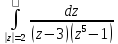
Изобразим область, по которой производится интегрирование:

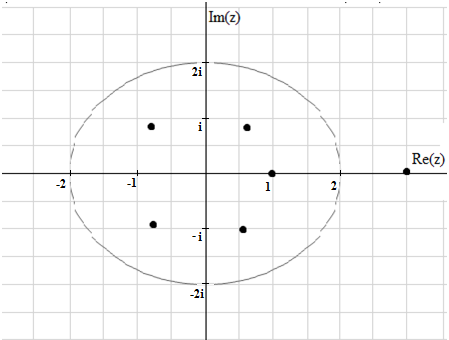
Определим особые точки приравняв знаменатель к нулю:

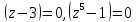
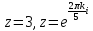
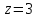– особая точка типа простой полюс. 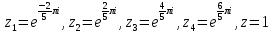– простые полюсы функции f(z), попадающие в контур интегрирования. Следовательно:

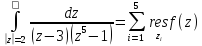
Согласно теореме т.1:

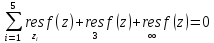
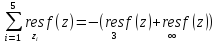
Вычет относительно бесконечности вычислим с помощью формулы (19):

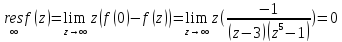
Значит исходные интеграл будет равен 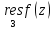с обратным знаком умноженный на 2πi. 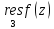найдем использую формулу (16):

2.3. Интеграл от по контуру .

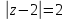Изобразим контур интегрирования:

Найдем особые точки подынтегральной функции:

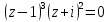
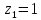–полюс третьего порядка и – полюс второго порядка. Точка z₁ попадает внутрь контура интегрирования, следовательно, согласно формуле (15):

Заключение

Из рассмотренных в работе примеров видно, что понятие и свойства вычетов позволяют вычислять интегралы от функций комплексного переменного с помощью теоремы о вычетах. При чем на практике для её применения удобнее использовать не определение вычета, а следствия из него.

Список литературы

1. Привалов И.И. Введение в теорию функций комплексного переменного. – М.: Наука, 1984.

2. Шабат Б. В. Введение в комплексный анализ. — М.: Наука, 1976.

3. Боярчук А.К. Функции комплексного переменного: теория и практика. – М.: Едиториал УРСС, 2001.

4. Высшая математика для начинающих физиков и техников. Зельдович Я.Б., Яглом И.М. М.: Наука, 1982.

14