2.3.Переход от волновой теории к законам геометрической оптики

Прежде необходимо обосновать условия, при которых электромагнитное поле будет удовлетворять законам геометрической оптики. Для этого решается уравнения Максвелла rot H = jωεЕ и rot Е = - j ωμ Н в области с неизменными параметрами ε и μ в следующем виде [5,6]:

Е = Е₀(x¸y¸z) е ^{– jк L(x¸y¸z)};

Н = Н₀(x¸y¸z) е ^{–jк L(x¸y¸z)}¸ (2.16)

где - Е₀, Н₀ есть комплексные векторные амплитуды;

- к = ω/с;

- L = n L(x¸y¸z) есть функция, определяющая волновые поверхности поля.

Чтобы найти уравнения, которым удовлетворяют Е₀, Н₀ и L, нужно подставить выражения (2.16) в уравнения Максвелла. После подстановки получаются Е₀ = - (к/ωε) ·(gradL x Н₀) + (1/jωε) rotН₀,

Н₀ = (к/ωμ)·(grad L x Е₀) – (1/ jωμ) rotЕ₀. (2.17)

Подставив значение Н₀ из второго уравнения в первое системы (2.17), можно получить

Е₀ = - (1/n²)[grad L( Е₀·gradL) - E₀·|gradL|²] + (1/jn²к)[rot (gradL х E₀) +

+ (gradL х E₀)] + (1/n²к²)·rot rotЕ₀ . (2.18)

Аналогично уравнению удовлетворяет также вектор Н₀, если ω → ∞, то и

к → ∞, следовательно, выражение (2.18) преобразится к виду

Е₀ |ω→ ∞ = - (1/n²)[gradL (E₀ gradL) - E₀ | gradL |²]. (2.19)

В выражении (2.19) и подобного выражения для Н₀ (2.18) соотношения будут выполняться при следующих условиях:

Е₀ grad L = 0; (2.20)

Н₀ grad L = 0; (2.21)

| grad L |² = n². (2.22)

Равенство, определенное выражением (2.22), совпадает с дифференциальным уравнением (2.10), которому удовлетворяет функция L. Из условий (2.20) и (2.21) вытекает, что векторы Е₀ и Н₀ перпендикулярны направлению распространения волновой поверхности, так как gradL в каждой точке поверхности L = соnst нормален к ней и, значит, направлен по лучу.

Таким образом, волновое электромагнитное поле в предельном случае при ω →∞ (или λ→ 0) вырождается в поле, удовлетворяющее законам геометрической оптики. При этом каждый бесконечно малый элемент волновой поверхности поля ведет себя как элемент фронта плоской волны.

2. 4. РЕШЕНИЕ ДИФРАКЦИОННЫХ ЗАДАЧ

2.4.1. Дифракция электромагнитной волны на теле произвольной формы.

Пусть на тело с поверхностью S падает электромагнитная волна, возбуждаемая удаленным источником Р (рис.2.4). Определить вторичное поле (рассеянное) [5,6].

S P

Рис. 2.4

Пусть дифракция электромагнитной волны на теле будет подчиняться законам геометрической оптики. Основанием для этого являются соотношения длины волны с размерами тела и радиусов кривизны его поверхности. Это значит, что длина волны много меньше размеров тела и радиусов кривизны. Тогда элемент фронта падающей волны на криволинейную граничную поверхность будет вести себя как элемент фронта плоской волны, падающей на плоскую поверхность. Однако законы геометрической оптики дают решение для области тени, где поле оценивается равным нулю. В действительности, поле там, безусловно, будет. Поэтому законы геометрической оптики целесообразно применять лишь для того, чтобы определить приближенные значения векторов вторичного поля на граничной поверхности, а затем, на основании методов волновой теории, рассчитать уже поле во всем пространстве. При этом на теневой части тела вектор поверхностной плотности тока равен нулю (δ_s = 0). Тело идеальный проводник. На освещенной стороне вектор плотности тока определится исходя из условия, что в каждой точке поверхности волна источника отражается по тем же законам, что и плоская волна, падающая на бесконечную, идеально проводящую плоскость, или, что

Н_{τ пад} = Н_{τ отр} , (2.23)

где Н_{τ пад} и Н_{τ отр} - касательные составляющие падающей и отраженной волн (рис. 2.5).

Н _пад n

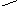Н_{τ пад} S

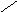
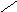
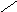
Рис. 2.5

С учетом нормали к поверхности можно записать для падающего вектора

Н_{τ пад} = n x (Н _пад х n ).

Аналогично можно записать для отраженного вектора

Н_{τ отр} = n х (Н _отр х n ).

Следовательно, выражение (2.23) может быть записано в виде

(Н _пад х n) = (Н _отр х n). (2.24)

Плотность тока на освещенной части тела, возбуждаемого полем падающей волны, равна δ_s = (Н _пад + Н _отр) х n

и с учетом равенства (2.24), получается

δ_s = 2 (Н_пад х n). (2.25)

Таким образом, приближенный закон распределения тока, возбуждаемого на поверхности проводящего тела при дифракции электромагнитной волны, имеет вид

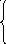
0 - на теневой части тела,

δ_s = (2.26)

2(Н_пад х n) - на освещенной части тела.

Зная распределение тока, несложно определить поле в дальней зоне через векторный электродинамический потенциал А.

Дифракция плоской электромагнитной волны на отверстии в плоском

проводящем экране

Пусть плоская волна с векторами

Е _пад = - х Е₀ е ^{– jкz};

и Н _пад = - у Н₀ е ^{– jкz}

падает на бесконечный проводящий экран, расположенный в плоскости z = 0. Требуется рассчитать электромагнитное поле, проникающее в переднее полупространство ( z ≥ 0) через отверстие прямоугольной формы с размерами сторон α и b (рис.2.6).

х х

П О z у

α

b

Е _пад

Рис. 2.6

Для расчета вторичного электромагнитного поля удобно использовать принцип эквивалентных токов в сочетании с законами геометрической оптики [5]. По законам геометрической оптики поле, проникающее за экран при падении на него плоской волны, представляется в виде пучка лучей, параллельных оси z, с поперечным сечением той формы, что и отверстие. При этом поле перед экраном имеет другую структуру, но необходимо найти приближенное распределение векторов поля в плоскости z = 0. Согласно закону распределение поля на отверстии должно совпадать с распределением падающей волны, а на остальной части, в зоне тени векторы должны равняться нулю. Причем, изложенное справедливо при условии, что размеры отверстия значительно больше длины падающей волны (α >λ; b >λ). Искажения поля появляются вблизи кромок отверстия и эти искажения тем меньше, чем меньше длина волны по сравнению с размерами отверстия. Кроме того, в зоне тени поле не обращается в нуль. В действительности, на экране по его освещенной части и по теневой поверхности течет электрический ток и, следовательно, касательная составляющая магнитного поля отлична от нуля. Однако проникающее поле в область тени невелико. В соответствии с изложенным, граничные условия для векторов Е и Н искомого поля в плоскости экрана (z = 0) можно записать в следующем виде

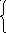
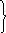- х Е₀ на S ₀;

Е =

0 на S ₁; (2.27)

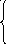
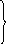
- у Н ₀ на S ₀;

Н =

0. на S ₁, (2.28)

где - S ₀ – площадь отверстия;

- S ₁ – теневая поверхность экрана.

На основании выражений (2.27) и (2.28) в плоскости z = 0 будут протекать поверхностные электрические δ_s и магнитные токи δ_{s м}

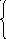
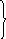х Е₀ - на S₀;

δ_s =

0. - на S₁; (2.29)

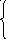
у Е₀ - на S₀;

δ_{s м} =

0 - на S₁. (2.30)

Таким образом, для определения поля, проникающего в пространство через отверстие, необходимо найти поле поверхностных электрических и магнитных токов. Подобная задача была рассмотрена при изучении элемента Гюйгенса.

Плоские дифракционные антенны

Дифракционная антенна представляет собой проводящую поверхность с отверстием или совокупностью отверстий, через которые излучается электромагнитное поле. Отверстие закрыто проводящими стенками, образующими вместе с отверстием внутреннюю полость. В этой полости помещается источник поля в виде штыря или рамки с током. Следовательно, излучение электромагнитных волн во внешнее пространство происходит в результате дифракции поля первичного источника на отверстии. Поэтому и с этим физическим явлением связано название дифракционной антенны. Если проводящая поверхность является плоскостью, то и антенна называется плоской, а отверстия для излучения получили название щелевых излучателей.

Задание для самопроверки знаний и умения

1. Какое явление называют дифракцией электромагнитных волн ?

2. Какие задачи решаются дифракционными методами?

3. Основное уравнение геометрической оптики.

4. Законы геометрической оптики.

5. Дифракция электромагнитного поля на теле произвольной формы.

6. Дифракция плоской электромагнитной волны на отверстии в плоском проводящем экране.

7. Примеры дифракционных антенн.