Линейная интерполяция.

При линейной интерполяции строится ломаная, которая проходит через точки (Xi;Yi), i=0,1,2,...,n, т.е. совпадающая с искомой функцией в узлах интерполирования и линейная на каждом участке(Xi;X_i+1) при i=0,1,2,...,n-1.

Ясно, что при Xi<=X<=X_i+1 значения построенной функции (X) будут вычисляться по формуле (X)=Yi+(X-Xi) (Y_i+1 -Yi)/(X_i+1 -Xi).

Упражнение 2.1 Составить программу для определения значения функции при линейной интерполяции.

Если сетка узлов достаточно плотная на отрезке [a,b], а функция f(X) гладкая, то точность этого метода вычисления приближенного значения функции f(X) вполне удовлетворительна, поэтому в инженерной практике метод линейной интерполяции весьма распространен. Однако, при решении других задач, таких, как задача численного дифференцирования, погрешности данного метода многократно возрастают и перестают быть удовлетворительными.

Интерполяция многочленом. Единственность интерполяционного многочлена n-й степени.

Другой вариант интерполирования - искать функцию в виде многочлена степени n:

(X)=P_n(X)=C_nXⁿ+C_n-1X^n-1+..... +C₁ X+C₀

Условия совпадения значений интерполирующей функции в точках Xi с величинами Yi примет вид системы: C₀+C₁X₁ +... +C_nX₁ⁿ=Y₁

C₀+C₁X₂ +... +C_nX₂ⁿ=Y₂

_{………………………………………….}

C₀+C₁X_n +... +C_nX_nⁿ=Y_n

(n+1)-го линейного уравнения с n+1 неизвестным.

Поскольку определитель этой системы является определителем Вандермонда и все числа Xi различны, то он отличен от нуля и, следовательно, искомый многочлен существует и единственен. В данном случае, так же как и в предыдущем, снимаются основные сложности, связанные с проблемой оптимального выбора среди функций, удовлетворяющих условиям интерполяции в узлах, однако остается вопрос о точности приближения.

Построение вспомогательных многочленов Лагранжа.

Для того, чтобы записать интерполяционный многочлен в форме Лагранжа, сначала строят вспомогательные многочлены L₀(X), L₁(X),..., Ln(X), каждый из которых является многочленом степени n и удовлетворяет условиям:

, i, j = 0,1,2,..,n.

У каждого из вспомогательных многочленов, тем самым, мы знаем n корней, например, у L₂(X) корнями являются X₀, X₁, X₃ ..., Xn. Kaк известно, многочлен Li(X) по корням можно записать в виде

Li(X)=Ai(X-X₀)...(X-X_i-1)(X-X_i+1)...(X-Xn)= Ai

Чтобы определить величину Ai, остается еще одно условие Li(Xi)=1, откуда:

Построение многочлена Лагранжа.

Зная вспомогательные многочлены, легко построить и искомый многочлен в виде их линейной комбинации:

В самом деле, степень Рn(х) не выше n, a подставляя в эту формулу значения Х=Хj, получаем: Рn (Xj)=Уj при j=0,1,2,...,n.

Поскольку ранее мы установили, что многочлен степени n, удовлетворяющий условиям интерполяции в узлах единственен, то построенный многочлен Рn(X) и является искомым. Окончательно, он запишется в виде:

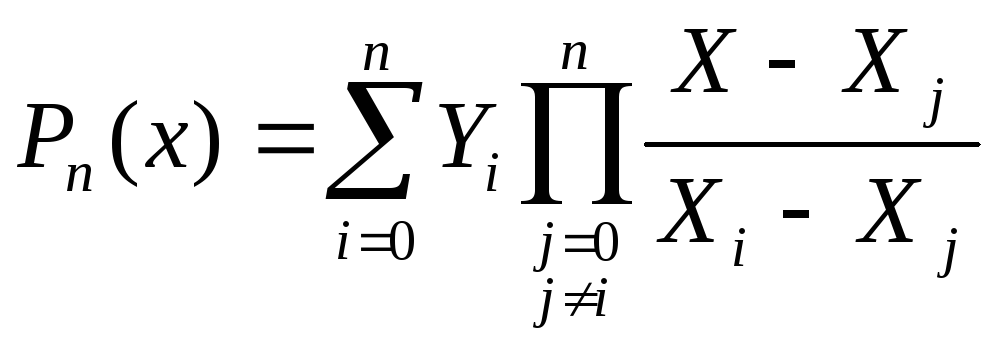
Упражнения: Пользуясь формулой (2.1) выписать интерполяционный многочлен в форме Ньютона для функции, заданной таблицей:

(2.2)	X	1	2	3	(2.3)	X	-1	0	1	2
	y	2	3	6		y	2	2	2	8

Оценка точности формулы (2.1) проводится при предположении, что исходная функция f(x) является (n+1) раз дифференцируемой и мы знаем максимум модуля ее (n+1)-ой производной M_n+1. Как уже отмечалось выше, без дополнительных ограничений на гладкость функции никаких оценок произвести нельзя.