
- •1 Вопрос
- •2 Вопрос
- •3 Вопрос
- •4 Вопрос
- •Теорема о необходимом и достаточном условии существования предела последовательности:
- •Свойства бесконечно малых и бесконечно больших последовательностей:
- •5 Вопрос
- •Монотонная функция:
- •6 Вопрос
- •Функция синус
- •Функция косинус
- •Функция тангенс
- •Функция котангенс
- •7 Вопрос
- •8 Вопрос
- •9 Вопрос
- •10 Вопрос
- •11 Вопрос
- •12 Вопрос
- •13 Вопрос
3 Вопрос
Арифметические операции над последовательностями, имеющими предел:
Дано: lim xn = a, lim yn = b при n→∞.
-
Сложение (xn+yn = a+b).
-
Вычитание (xn-yn = a-b).
-
Умножение (xn*yn = a*b).
-
Деление (xn/yn = a/b, yn и b ≠ 0).
Доказательство:
1. Из определений последовательностей:
ε
> 0,
![]() n1(ε),
n1(ε),
![]() n > n1:
n > n1:
![]()
![]()
ε
> 0,
![]() n2(ε),
n2(ε),
![]() n > n2:
n > n2:
![]()
![]()
Получим:
![]() .
Доказано
.
Доказано
2. Аналогично первому.
3.![]() Т.к.
последовательность сходящаяся, то она
ограниченна =>
Т.к.
последовательность сходящаяся, то она
ограниченна =>
![]() M>0,
M>0,
![]() n:
|xn|
n:
|xn|![]() M,
M
M,
M![]() |b|
:
|b|
:
|xn-a|
<
![]() ;
;
|yn-b|
<
![]() ,
где число M выберем позже.
,
где число M выберем позже.
![]() <
M*
<
M*![]() +
M*
+
M*![]() =
=
![]() .
.
4. Аналогично 3, только не забыть, что yn и b ≠ 0, иначе деление на ноль.
4 Вопрос
Бесконечно малая:
Последовательность
an называется бесконечно
малой, если
![]()
Бесконечно большая:
Последовательность
an называется бесконечно
большой, если
![]()
Теорема о необходимом и достаточном условии существования предела последовательности:
Для
того, чтобы число a было
lim xn,
необходимо и достаточно, чтобы xn
= a +
![]() n,
где
n,
где
![]() n
– б.м.
n
– б.м.
Доказательство:
-
Необходимость: Дано: xn→a. Докажем, что при xn→a существует
 n,
такое,
n,
такое,
что
xn = a
+
![]() n:
n:
![]() n
= xn –
a,
n
= xn –
a,
lim
![]() n
= lim xn –
a, при n→a
n
= lim xn –
a, при n→a
lim xn – a, при n→a равняется lim xn – lim a = a – a = 0. Доказано.
-
Достаточность: Дано: xn = a +
 n:
n:
Доказать: xn = a.
lim
xn =
lim(a +
![]() n)
при n→∞
равняется lim a + lim
n)
при n→∞
равняется lim a + lim
![]() n
= a + 0 = a. Доказано.
n
= a + 0 = a. Доказано.
Свойства бесконечно малых и бесконечно больших последовательностей:
-
Если
 n
– беск. малое,
n
– беск. малое,
 n
≠ 0, то
n
≠ 0, то
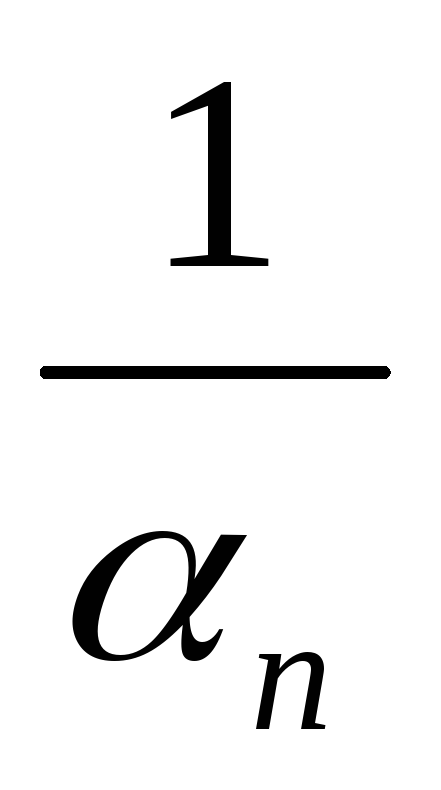 - бесконечно большое.
- бесконечно большое.
Доказательство:
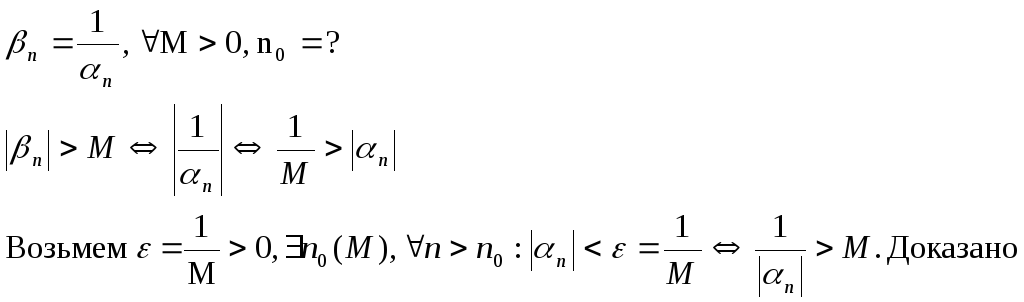
-
Если
 n
– беск. большое,
n
– беск. большое,
 n
≠ 0, то
n
≠ 0, то
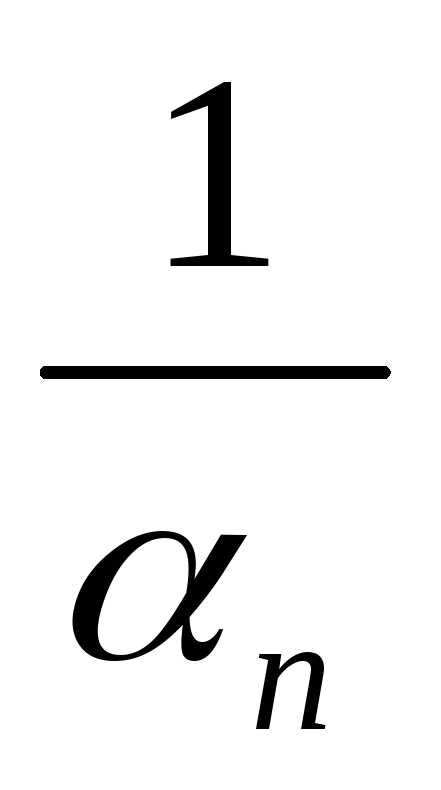 - бесконечно малое.
- бесконечно малое.
Доказательство: аналогично первому
-
Произведение б.м. последовательности на ограниченную последовательность есть б.м. последовательность.
Доказательство:
Дано:
![]()
Докажем,
что
![]() :
:
Возьмем
![]()
-
Если
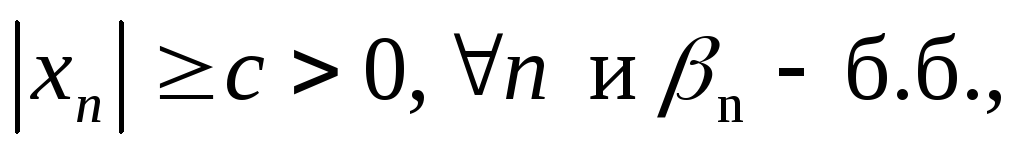 то
то
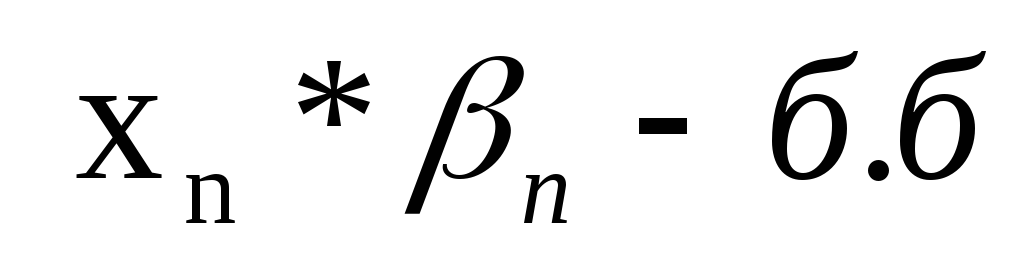 .
Только если последовательность отделима
от нуля, т.е. c > 0.
.
Только если последовательность отделима
от нуля, т.е. c > 0.
Доказательство: нет.
5 Вопрос
Понятие функции:
Определение: Отношение f между А и В, при котором каждому элементу из А соответствует не более одного элемента из В называется функцией.
Способы задания функции:
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
Монотонная функция:
Функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Ограниченная функция:
Функция называется ограниченной, если существует такое положительное число M,
что
|f ( x )|![]() M для всех значений x .
Если
такого числа не существует, то функция
- неограниченная.
M для всех значений x .
Если
такого числа не существует, то функция
- неограниченная.
Периодическая функция:
Функция, повторяющая свои значения через какой-то ненулевой период, то есть не меняющая своего значения при добавлении к аргументу фиксированного ненулевого числа (периода).
Называется
периодической, если
![]()
Четная функция:
Функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
Нечетная функция:
Функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
