§ 8. Линейные преобразования (операторы).

8.8. Найти собственные числа и собственные векторы линейного преобразования, заданного в некотором базисе матрицей. Найти матрицу оператора в базисе из собственных векторов.

Общие сведения и расчётные формулы: для выполнения задания необходимо знать:

Если задана матрица линейного преобразования, то можно записать характеристическую матрицу и характеристический многочлен этого преобразования:

= → = =0.

Решая уравнение: =0, находят характеристических корней этого многочлена:

=.

Эти корни являются собственными значениями линейного преобразования , используя которые, можно записать для некоторого вектора :

=,

вектор в этом случае называют собственным вектором преобразования , соответствующим собственному значению .

Для нахождения собственных векторов линейного преобразования , соответствующих характеристическому корню , необходимо найти ненулевые решения системы линейных уравнений:

=·=0. (1)

Если в качестве базиса линейного векторного пространства выбрать все собственные векторы, то матрица линейного преобразования будет иметь в этом базисе самый простой вид, а именно:

.

Примеры (и образец оформления):

Пример–1: Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей: =. Найти матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования.

Решение:

Схема решения: 1) составляем характеристический многочлен и находим его корни;

2) составляем систему уравнений для нахождения собственных векторов;

3) находим поочередно для каждого собственного значения собственные векторы линейного преобразования.

4) строим матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования.

1). В нашем случае характеристический многочлен имеет вид:

== ––(2+) = –(+1)³,

его корни: = –1, кратности 3.

2). Составляем систему уравнений для нахождения собственных векторов:

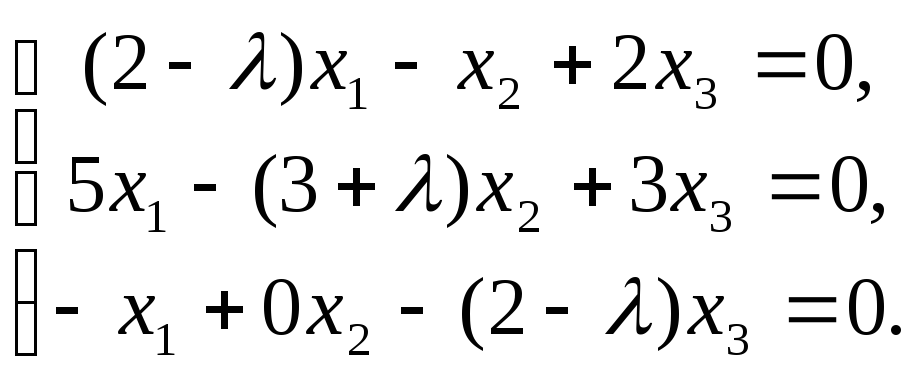== (1)

3). Находим собственные векторы линейного преобразования, используя общую запись системы уравнений в виде (1) для = –1:



где x₃ свободная неизвестная; пусть x₃ = –с, тогда x₁ = с, x₂ = с, получаем: = с(1,1,–1).

4). Строим матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования: .

Ответ: собственные значения: = –1, кратности 3; собственные векторы линейного преобразования имеют вид: = с(1,1,–1), где с  0. Матрица преобразования в базисе, составленном из собственных векторов этого преобразования: .

Пример–2: Найти собственные значения и собственные векторы линейного преобразования, заданного матрицей: =. Найти матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования.

Решение:

Схема решения: 1) составляем характеристический многочлен и находим его корни;

2) составляем систему уравнений для нахождения собственных векторов;

3) находим поочередно для каждого собственного значения собственные векторы линейного преобразования.

4) строим матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования.

1). В нашем случае характеристический многочлен имеет вид:

=== –(–2) =

= (–2) (–1) –3(λ–2)= – (+1)( +2)( –2),

его корни: = –1, = –2, = 2.

2). Составляем систему уравнений для нахождения собственных векторов:

== (1)

3). Находим собственные векторы линейного преобразования, используя общую запись системы уравнений в виде (1):

для = –1: 

где свободная неизвестная; пусть =, тогда =, =, получаем: =·(1,1,1).

для = –2: 

где свободная неизвестная; пусть =3, тогда =2, =3, получаем: =·(2,3,3).

для = 2: 

где свободная неизвестная; пусть =7, тогда =4, =, получаем: =·(4,1,7).

4). Строим матрицу линейного преобразования в базисе, составленном из собственных векторов этого преобразования: .

Ответ: собственные значения: = –1, = –2, = 2; собственные векторы линейного преобразования имеют вид: =·(1,1,1), где  0; =·(2,3,3), где  0; =·(4,1,7), где  0. Матрица преобразования в базисе, составленном из собственных векторов этого преобразования: .

Варианты индивидуальных заданий:

Вар.	Задание:	Вар.	Задание:	Вар.	Задание:
1.		2.		3.
4.		5.		6.
7.		8.		9.
10.		11.		12.
13.		14.		15.
16.		17.		18.
19.		20.		21.
22.		23.		24.
25.		26.		27.
28.		29.		30.