
- •Оптимальные и адаптивные системы (1 четверть).
- •Введение.
- •Глава 1. Принцип максимума Понтрягина (пмп).
- •Методика пмп.
- •Связь оптимального управления с энергией, запасаемой в объекте.
- •Теорема об n-интервалах.
- •Определение моментов переключения управляющих функций. Метод стыковки решения.
- •Задача об управлении консервативным объектом.
- •Аналитический синтез оптимальных регуляторов по квадратичному критерию качества.
- •Дискретная форма вариационной задачи. Принцип оптимальности Беллмана.
- •Непрерывная задача динамического программирования.
- •Глава 2. Общая характеристика адаптивных систем. Их классификация.
- •Типы самонастраивающихся систем (снс).
-
Аналитический синтез оптимальных регуляторов по квадратичному критерию качества.
Пусть
мат модель ОУ задана в переменных
состояния:
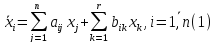
В
векторном виде:
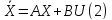
X – n-мерный вектор переменных состояния.
A – квадратная матрица
B - n×r матрица
U – r-мерный вектор управляющих воздействий.
Для этого объекта необходимо синтезировать регулятор оптимальный с точки зрения квадратичного критерия:
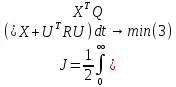
Q – матрица весовых коэффициентов (gij – коэффициенты при xixj)
R –матрица r×r (rij коэффициенты при uiuj)
Обычно матрицы Q и R диагональные.
Рассмотрим пример.
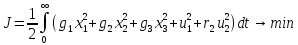
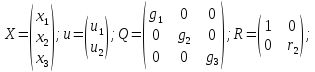
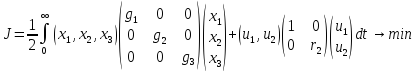
Задачу (2) и (3) решим с помощью ПМП.
-
Введем вспомогательную переменную и составим расширенную систему.
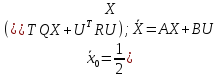
-
Составим функцию Гамильтона.
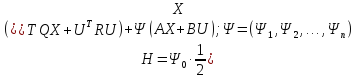
Функция
Н не зависит от
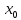 ,
поэтому
,
поэтому
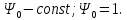
-
Решается задача H→max.
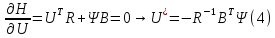

-
Определим функцию Ψ из системы сопряженных уравнений.
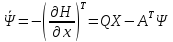
Функцию
Ψ будем искать в виде
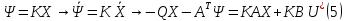
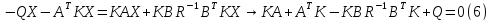
Уравнение (6) называется алгебраическим уравнение Рикати. Уравнение Рикати позволяет определить элементы матрицы К. Матрица К является симметричной. Уравнение Рикати является нелинейным, поэтому содержит несколько решений. Из этих решений выбирается одно, удовлетворяющее условию Сильвестра.
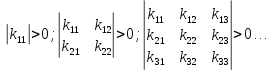
-
Дискретная форма вариационной задачи. Принцип оптимальности Беллмана.
Функционал
вариационной задачи:
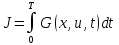 при замене подынтегральной функции G
ломаной может быть представлен в
дискретном виде:
при замене подынтегральной функции G
ломаной может быть представлен в
дискретном виде:
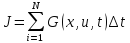
В
этом случае задача поиска экстремума
J
заменяется задачей мат программирования
поиска экстремума функций N-переменных
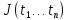 .
Чем больше N,
тем точнее решение. Но с увеличением N
возрастает сложность решения задачи,
поэтому Беллманом разработана методика
решения задач управления многошаговая,
мат аппаратом при этом является
динамическое программирование. Рассмотрим
задачу управления как многошаговую.
.
Чем больше N,
тем точнее решение. Но с увеличением N
возрастает сложность решения задачи,
поэтому Беллманом разработана методика
решения задач управления многошаговая,
мат аппаратом при этом является
динамическое программирование. Рассмотрим
задачу управления как многошаговую.
На
i-том
шаге управления под действием управления
Ui
объект переводится из состояния Xi-1
в состояние Xi.
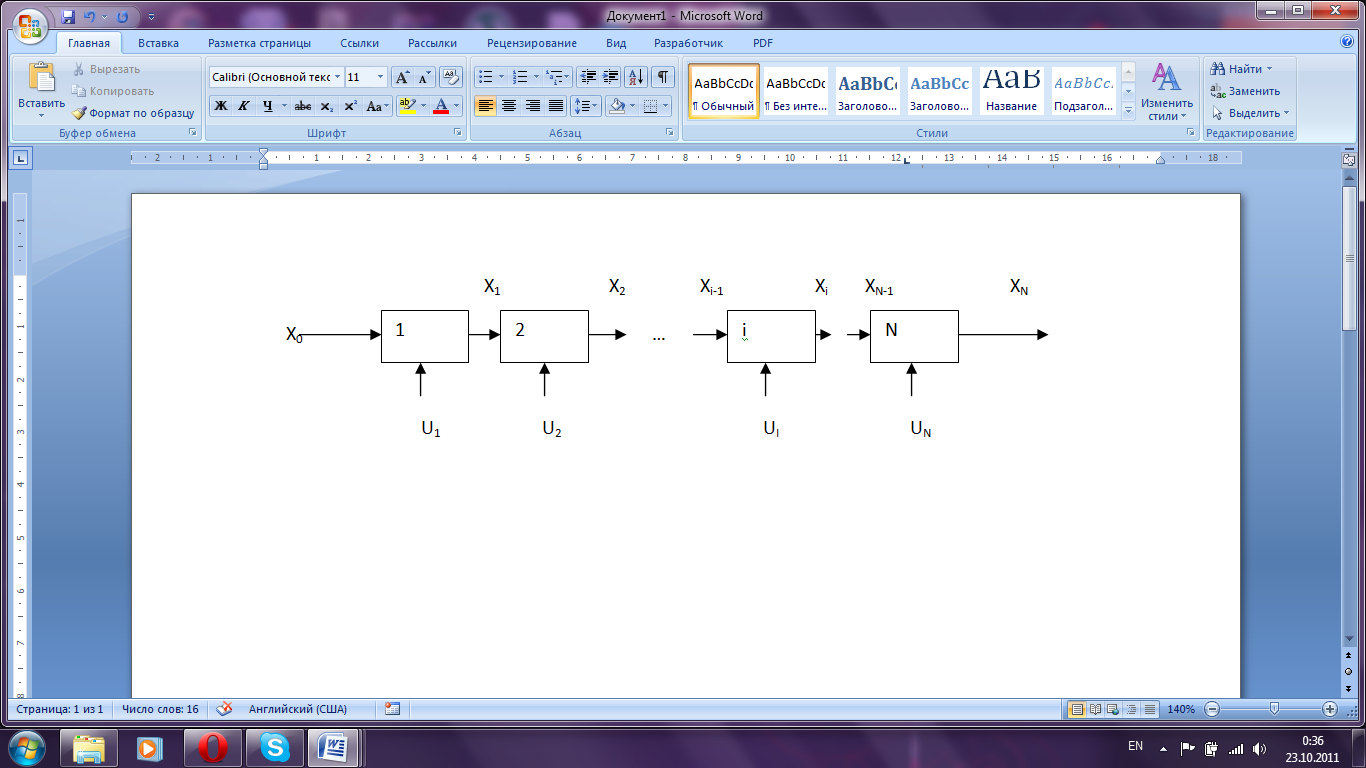
Эффективность
управления на каждом шаге оценивается
функцией потери r(xi,
u).
Эффективность всего управления:
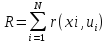 .
Задача состоит в определении такой
стратегии управления U*=(U1…UN),
которая переводила бы объект из X0
в XN
и при этом обеспечивала бы минимальные
функции потерь R.
.
Задача состоит в определении такой
стратегии управления U*=(U1…UN),
которая переводила бы объект из X0
в XN
и при этом обеспечивала бы минимальные
функции потерь R.
Введем понятия fk(xk) – минимальные потери, при переходе из состояния xk в состояние xn.
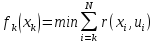
Поставленная задача решается на основе принципа оптимальности Беллмана: не зависимо от того каким образом система пришла в данное состояние, управление на данном шаге должно быть таким, чтобы суммарные потери на данном шаге + минимальные потери на всех последующих шагах были минимальными.
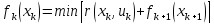 - рекуррентное
соотношение Беллмана, которое выражает
принцип оптимальности. Это соотношение
позволяет решать задачу с последнего
шага. Полагаем k=N-1
- рекуррентное
соотношение Беллмана, которое выражает
принцип оптимальности. Это соотношение
позволяет решать задачу с последнего
шага. Полагаем k=N-1
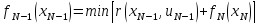
Для всех состояний XN-1 определяется условно-оптимальное управление UN-1. Затем полагаем k=N-2.
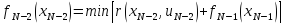
Определяется условно-оптимальное управление UN-2.
Процедура
продолжается до начального состояния
X0:
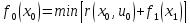 которая известна.
которая известна.
-
Непрерывная задача динамического программирования.
Принцип оптимальности Беллмана может быть применен и для решения непрерывных задач управления:
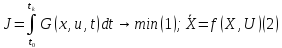
Эта задача при замене dt на Δt может быть представлена в дискретном виде:

Для данной задачи функция минимальных потерь имеет вид:
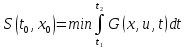
Минимальные
потери при движении системы из
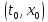 в конечное состояние.
в конечное состояние.
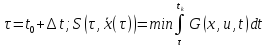
В
соответствии с принципом оптимальности:
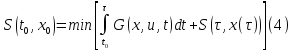
Функцию
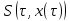 разложим в ряд вблизи точки
разложим в ряд вблизи точки
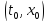 :
:
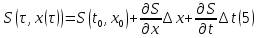
Подставим
(5) в (4):

Подставляем
(3) в (6):
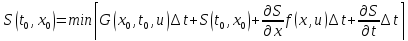

Функция в квадратных скобках равна 0, если она минимальна, поэтому последнее выражение эквивалентно системе:
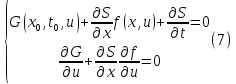
Выражение (7) называется функциональным уравнением Беллмана для непрерывной задачи управления.
Если
верхний предел
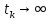 :
:
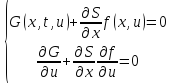
Метод динамического программирования позволяет синтезировать системы не только оптимальные, но и устойчивые, поскольку функция минимальных потерь S является функцией Ляпунова.
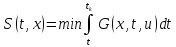 -
знакоопределенная положительная
функция.
-
знакоопределенная положительная
функция.
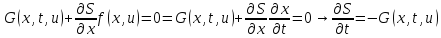 -
знакоопределенная отрицательная
функция.
-
знакоопределенная отрицательная
функция.
