3. Дисперсия случайной величины и ее свойства.

Многие случайные величины имеют одинаковое математическое ожидание, но различные возможные значения. Поэтому одного математического ожидания недостаточно для характеристики случайной величины.

Пусть доходы Х и Y(в долларах) двух фирм заданы распределениями:

X	800	1000		Y	400	1850
	0,1	0,9			0,6	0,4

Вычислив их ожидаемые доходы, получим M(X) = 980$ и M(X) = 980$, т.е. они равны, хотя возможные доходы и их вероятности различны.

Чтобы оценить, как рассеяны возможные значения случайной величины относительно ее математического ожидания, пользуются числовой характеристикой, которую называют дисперсией.

Определение. Дисперсией случайной величины Х называется неотрицательное число D(X), определяемое формулой

, если Х – дискретная случайная

величина,

, если Х – непрерывная случай-

ная величина.

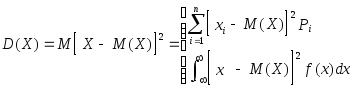
Иногда удобно пользоваться другой формулой, которую можно получить, если воспользоваться свойствами математического ожидания,

.

Дисперсия существует, если ряд (соответственно интеграл) сходится.

Неотрицательное число называется средним квадратическим отклонением случайной величины Х. Оно имеет размерность случайной величины Х и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. Величину иногда называют стандартным отклонением.

Случайная величина называется центрированной, если . Случайная величина называется нормированной (стандартной), если .

Продолжим пример. Вычислим дисперсию доходов двух фирм:

Сравнивания дисперсии, видим, что доход второй фирмы варьирует больше, чем первой.

Свойства дисперсии.

1. Дисперсия постоянной величины равна нулю, т.е. 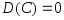, если 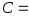константа. Это очевидно, так как постоянная величина имеет математическое ожидание, равное постоянной величине, т.е. .

2. Постоянный множитель C можно вынести за знак дисперсии, предварительно возведя его в квадрат.

Действительно,

3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией, т.е.

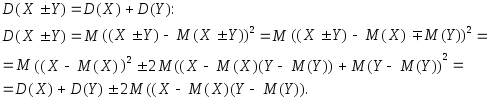
Выражение называется ковариацией величин Х и Y (см. Тема 4, §2). Для независимых случайных величин ковариация равна нулю, т.е.

Используя это равенство, можно пополнить список свойств математического ожидания. Если случайные величины Х и Y независимы, то математическое ожидание произведения равно произведению математических ожиданий, а именно:

Если случайная величина преобразована линейно, т.е. , то

.

Пример 1. Пусть производится n независимых испытаний, вероятность появления события А в каждом из которых постоянна и равна p. Чему равна дисперсия числа появлений события А в этих испытаниях?

Решение. Пусть – число появления события А в первом испытании, – число появления события А во втором испытании и т.д. Тогда общее число наступления события А в n испытаниях равно

.

Воспользовавшись свойством 3 дисперсии, получим

Здесь мы воспользовались тем, что , i = (см. примеры 1 и 2, п.3.3.1.).

Пример 2. Пусть Х – сумма вклада (в долларах) в банке – задана распределением вероятностей

Х	20	40	60	80	100	120
i =	0,01	0,03	0,10	0,30	0,5	0,06

Найти среднюю сумму вклада и дисперсию.

Решение. Средняя сумма вклада равна математическому ожиданию

.

Для вычисления дисперсии воспользуемся формулой

,

D(X) = 8196 – 7849,96 = 348,04.

Среднее квадратическое отклонение